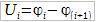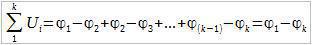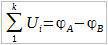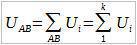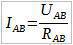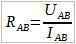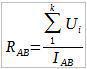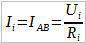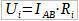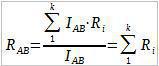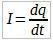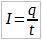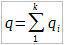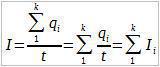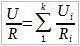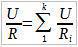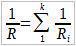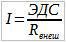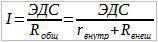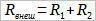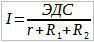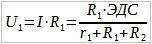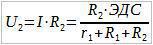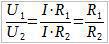Електрично коло и електрична шема
Електрично коло, то је скуп елемената и уређаја кроз које протиче струја. Електромагнетни процеси који се дешавају унутар електричног кола описују се уз помоћ појмова јачине струје и напона.
Електрична шема представља цртеж на којем су уз помоћ посебних ознака представљени елементи електричног кола.
Погледајмо сада два основна елемента електричних кола: изворе електромоторне силе и отпорнике.
Отпорници
Отпорници су елементи електричних кола који поседују сталну или промењиву отпорност. Користе се код линеарног мењања струје у напон или напона у струју, као и код ограничења и апсорпције електричне енергије. На електричним шемама отпорници се представљају на следећи начин:
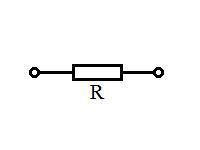
Затим хајде да погледамо основне карактеристике и параметре реалних отпорника:
- Нормална отпорност представља главни параметар који показује отпорност отпорника без учитавања грешке која настаје при производњи (случајна величина) и при собној температури (око 20 степени целзијуса)
- Граница дисипације снаге - показује максималну допуштену вредност диспације снаге при којој отпорник ради како треба
- Температурни коефицијент отпорности - показује измену реалне отпорности отпорника при измени температуре
- Тачност - максимално могуће одступање реалне отпорности од номиналне . Мери се у процентима од номиналне отпорности.
- Отпорност на влагу и топлоту - параметри који показују могућност коришћења отпорника у агресивним срединама: повишена температура и висока влажност
Затим погледајмо и редно и паралелно повезивање отпорника:
Редно повезивање отпорника

Замислите да у неком делу кола A-B, у којем се налазе редно повезани отпорници R1...Rk, тече струја I. Потребно је отдедити општу отпорност и напон на датом делу кола.
За почетак нађимо напон на делу A-B. Како у колу нема извора електромоторне силе то по Омовом закону напон на i-ом делу кола износи:
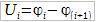
Саберимо напон на свим деловима кола (на свим отпорницима), треба да се добије:
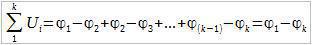
Приметите да је Ф1 = Фa, а Фk = Фb, и тада следи:
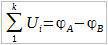
Разлика потенцијала тачака A и B по дефиницији (с обзиром да је елктромоторна сила на делу A-B равна нули) напон на делу A-B.
Добија се следеће:
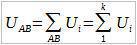
Сада се позабавимо општи отпором на делу A-B.
Напишимо Омов закон за део кола A-B:
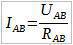
Из те формуле изразимо отпорност Rab:
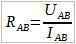
Затим, присетимо се да је напон на делу A-B једнак суми напона на сваком појединачном отпорнику:
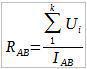
Сада напишимо Омов закон за сваки отпорник:
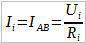
Одавде:
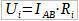
На крају, убацујемо претходни израз у формулу за Rab:
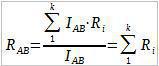
Закључак: Општа отпорност дела кола код редног везивања отпорника је једнака суми отпорности отпорника који улазе у то коло (Код редног везивања отпорности се сабирају.).
Паралелно везивање отпорника
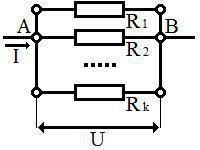
Пре него што пређемо на конкретан задатак увешћемо додатне појмове:
Чвор је део кола у којем се секу два или више проводника.
Замислимо да до чвора A долази струја I (из закона одржања количине наелектрисања следи да из чвора В излази иста та струја). Потребно је одредити еквивалентну отпорност дела кола A-B.
Присетите се да је:
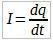
Размотримо довољно мали интервал времена на којем можемо узети да је струја стална и тада је:
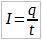
Струја у делу A-B једнака је односу опште количине наелектрисањ q, која је прошла кроз дати део кола за време t до тог времена.
У чвору A струја ће се разделити на k - делова. Количина наелектрисања ће пролазити кроз сваки отпорник. Замислимо да за време t кроз отпорник R1 проће количина наелектрисања q1, а кроз R2 - q2, ... , Rk - qk. Како се испољава закон одржања количине наелектрисања:
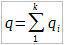
Разделимо оба израза са t. Тада се добија:
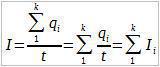
Добијамо да је струја која улази у чвор једнака суми струја које излазе из њега или тачније речено: Алгебарска сума струја, које се секу, у сваком чвору било којег кола је равна нули - Прво Кирхофово правило.
Затим примењујемо Омов закон:
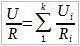
Приметимо да је напон на свим отпорницима једнак и износи U, како је Ui = Фa - Фb. Добијамо:
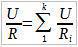
Затим поделимо израз са U:
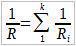
За резултат добијамо закон по којем се иурачунава еквивалентна отпорност код паралелно везаних отпорника.
Закључак: Величина обрнута отпорности дела кола код паралелно повезаних отпорника једнака је суми величина обрнутих отпорности за сваки отпорник.
Извор еллектромоторне силе
Извор електромоторне силе (идеалан извор напона) представља елемент електричног кола код којег унутрашњи напон не зависи од струје која кроз њега протиче. Електромоторна сила извора се задаје иликао константна величина или у функцији од времена или спољашње контроле. Идеални извор електромоторне силе графички се представља на следећи начин:
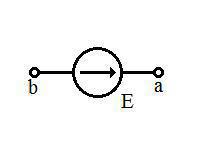
У пракси идеални извор електромоторне силе не постоји. Хајде да се сами убедимо. Напишимо Омов закон за цело коло:
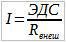
Приметимо да ако се спољашња отпорност смањује до нуле, добија се бесконачан раст струје што је физички немогуће. На основу овога уведен је појам реалног извора напона.
Реалан извор напона је елемент електричног кола који има отпорност r на којем делује извот електромоторне силе. Означава се на следећи начин:
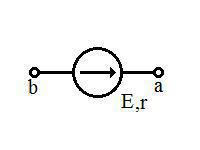
Реални извор напона може бити представљен као редно везивање извора електромоторне силе и отпорника r:
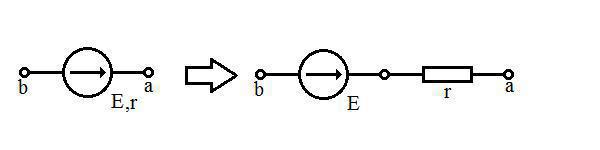
// овде треба написати о смеру електромоторне силе //
Раздвајач напона
Раздвајач напона је уређај код кога су улазни и излазни напон повезани коефицијентом размене a, 0 < a < 1.
Размотримо уређај које раздваја резистивни напон:
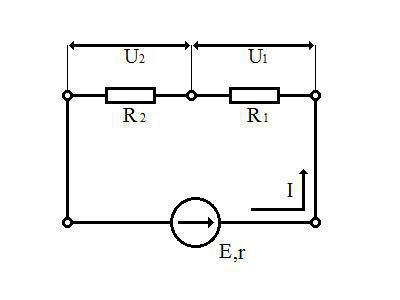
Замислимо да се електрично коло састоји из извора електромоторне силе (E,r) и два отпорника R1 и R2. У колу тече струја I. Потребно је наћи однос напона на отпорницима и њихову суму.
Напишимо Омов закон за цело коло:
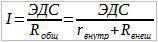
Отпорност извора електромоторне силе нам је познато, оно је једнако r. Отпорници R1 и R2 су редно везани и зато ћемо сабрати њихове отпорности:
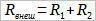
Струја I, која протиче кроз коло је једнака:
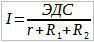
Сада применимо Омов закон за део кола на отпорнике R1 и R2:
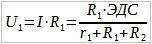
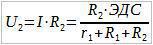
Поделимо U1 са U2:
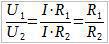
Однос напона U1 и U2 је раван односу отпорности R1 и R2.
Даље саберимо U1 и U2. Добијамо да је U12 - напон спољашњег дела кола:
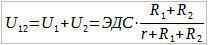
Ако је r довољно мало онда је напон на спољашњем делу кола практично једнак електромоторној сили.
Задаци
-
Унутрашња отпорност извора електромоторне силе
Опис вежбе:
1) Повежите лабораторијски извор струје са волтметром (цртеж ниже). Уз помоћ ручице регулатора (налази се на извору струје) мењајте напон на волтметру док се не укаже вредност од 9 волти. Како је унутарња отпорност извора струје мала (<< 1 Ома), а отпорност волтметра довољно велика (~10 МОм), то ће напон на њему практично бити једнак електромоторној сили извора:
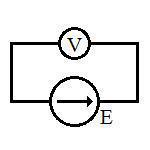
2) Направите електрично коло које ће се састојати из извора електромоторне силе (лабораторијски извор струје), промењивог отпорника, сталног отпорника R, волтметра (мултиметар у режиму мерења напона) и кључа К (отвореног) као на следећој шеми:
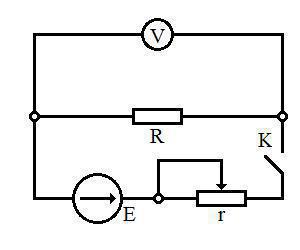
3) Уз помоћ промењивог отпорника установите унутарњу отпорност извора електромоторне силе. Ради тога узмите још један мултиметар и подесите га у режим мерења отпорности. Повешите његове игле са промењивим отпотником r. Сада установите отпорност отпорника:
А) 0 Ом - унутарња отпорност је једнака отпорности извора струје << 1 Ом.
Б) 30 Ом - унутарња отпорност је примерно једнака отпорности батерије
В) 100 Ом - унутарња отпорност довољно лошег извора
После установе отпорности у примерима под А), Б), В), потребно је искључити мултиметар, који смо користили за мерење отпорности.
4) Затим је потребно:
Затворити кључ K. Уз помоћ болтметра измерите напон на отпорнику R у случајевима A, Б и B. Анализирајте добијене резултате и на основу тога што сте видели донесите закључак о унутарњим отпорностима извора.
5) Фотографишите и поређајте по реду етапе вежбе.
6) Попуните таблицу напона у случајевима А,Б,В.
-
Раздвајач напона
Опис вежбе:
1) Направире електрично коло које се састоји из извора електромотроне силе, два редно везана отпорника R1, R2 и волтметра (мултиметар у режиму мерења напона) као што је приказано на слици:
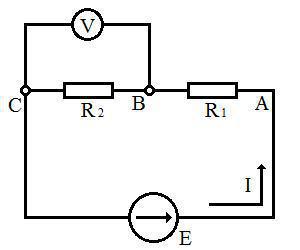
За извор узмите лабораторијски извор (подесите га на 15 волти).
Користите отпорнике R1 и R2 са отпорностима од:
А) 1КОм, 1КОм.
Б) 1КОм, 2КОм.
В) 1КОм, 5КОм.
Г) 1КОм, 10КОм.
2)За све понуђене варијанте А-Г уз помоћ мултиметра измерите напон на делу С-B. Анализирајте добијене резултате. У којем односу отпорници деле напон?
3) Фотографишите и поређајте по реду етапе вежбе.
4) Попуните таблицу напона у случајевима А-Г.