Оглавление 
 
Описание
Возбуждение волноводов заданными источниками. Соотношение ортогональности мод волновода.

Для того, что бы в реальном волноводе существовали электромагнитные волны, необходимо передать ему энергию, при этом нужно заметить, что поля могут возбуждаться переменными зарядами. Возбуждения волноводов заданными сторонними источниками основанно на разложениях возбуждаемого электромагнитного поля по собственным волнам волновода. 


Лемма Лоренца
 
Рассмотрим в общем случае неоднородное пространство.


Пусть в этом пространстве задано два распределения полей, соответствующие токам:


Запишем уравнения Максвелла для комплексных амплитуд, в который входят как электрические, так и магнитные токи.


Просуммируем полученные соотношения, перейдя к двум выражениям:


Проссумировав еще раз соответствующие компоненты и применяя равенство:


Лемма Лоренца в дифференциальной форме:


Проинтегрируем полученное выражение по обьему V, ограниченному поверхностью S. Затем воспользуемся формулой Гаусса-Остраградского и получим лемму Лоренца в интегральной форме.


Лемма Лоренца, гласит, что существует некая перекрестная связь между полями и токами.
Перейдем к волноводу.
 
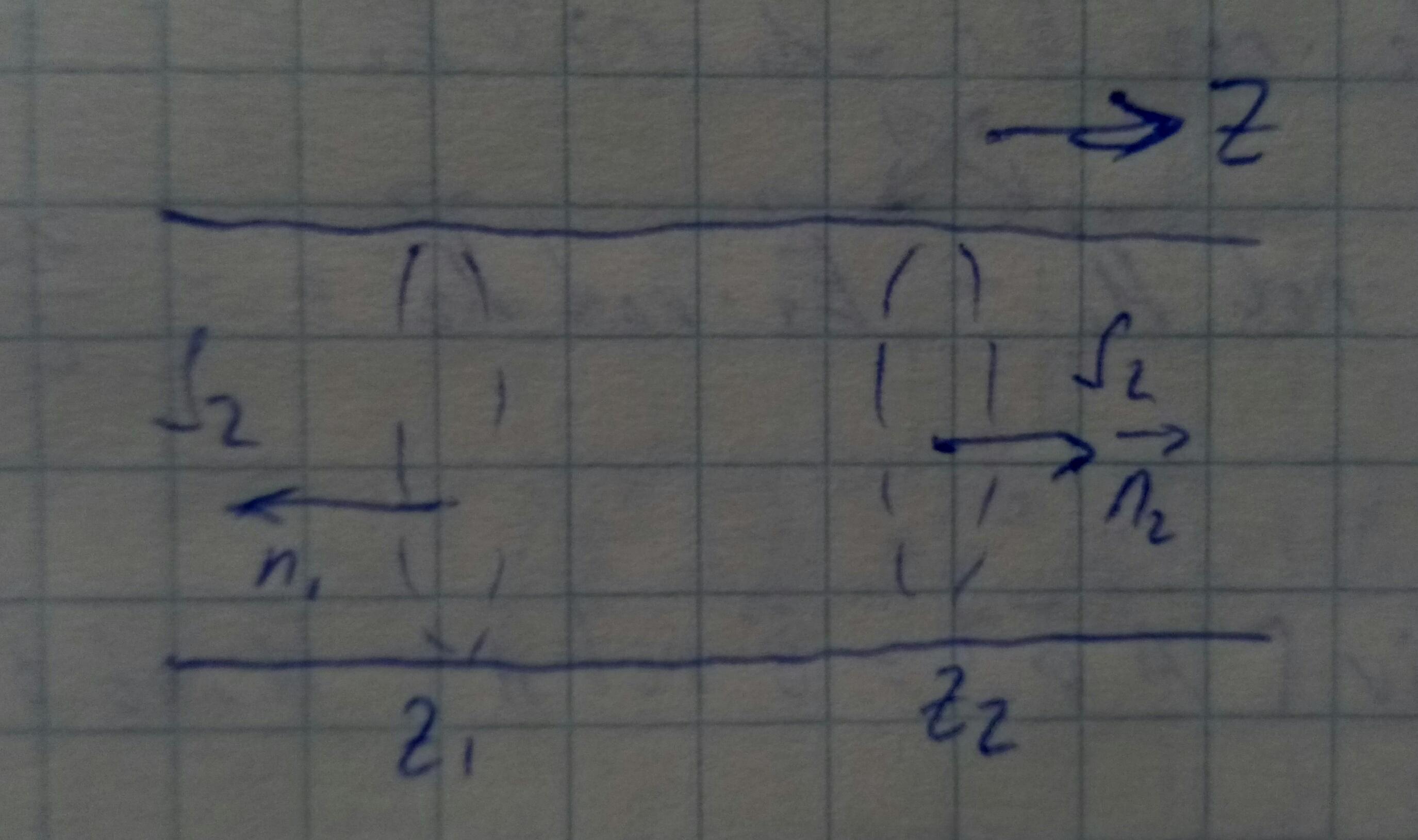
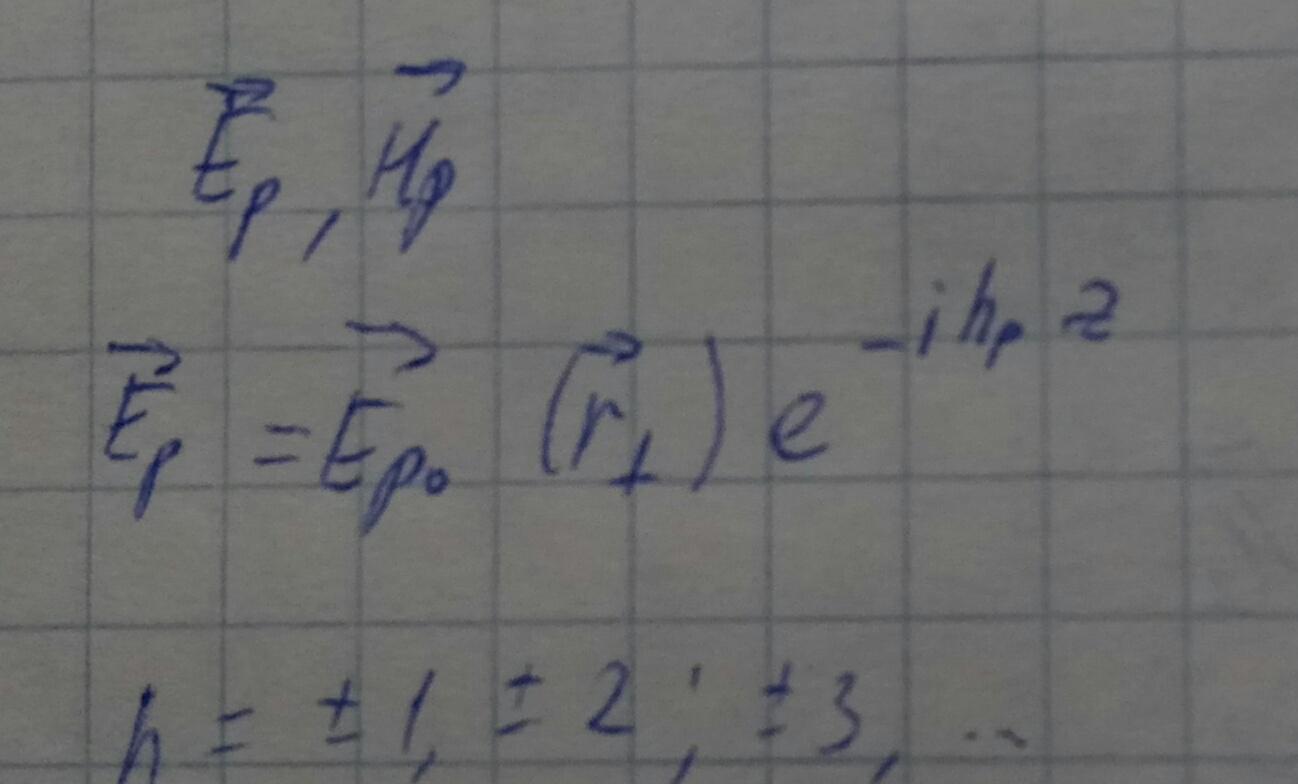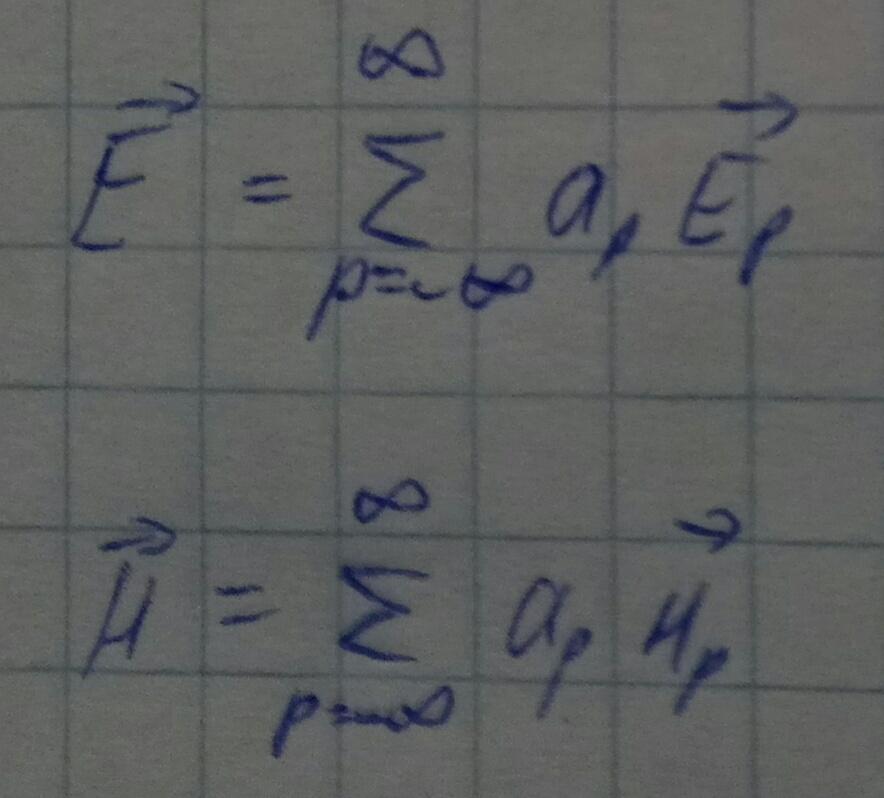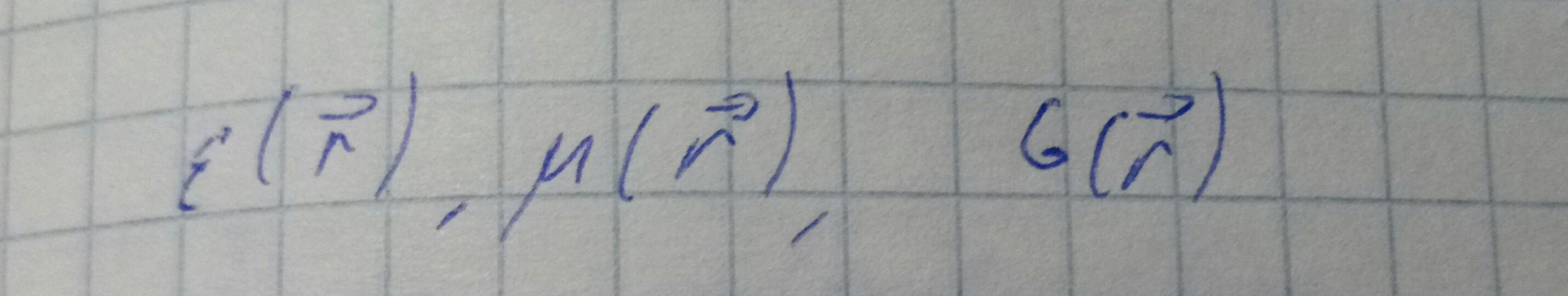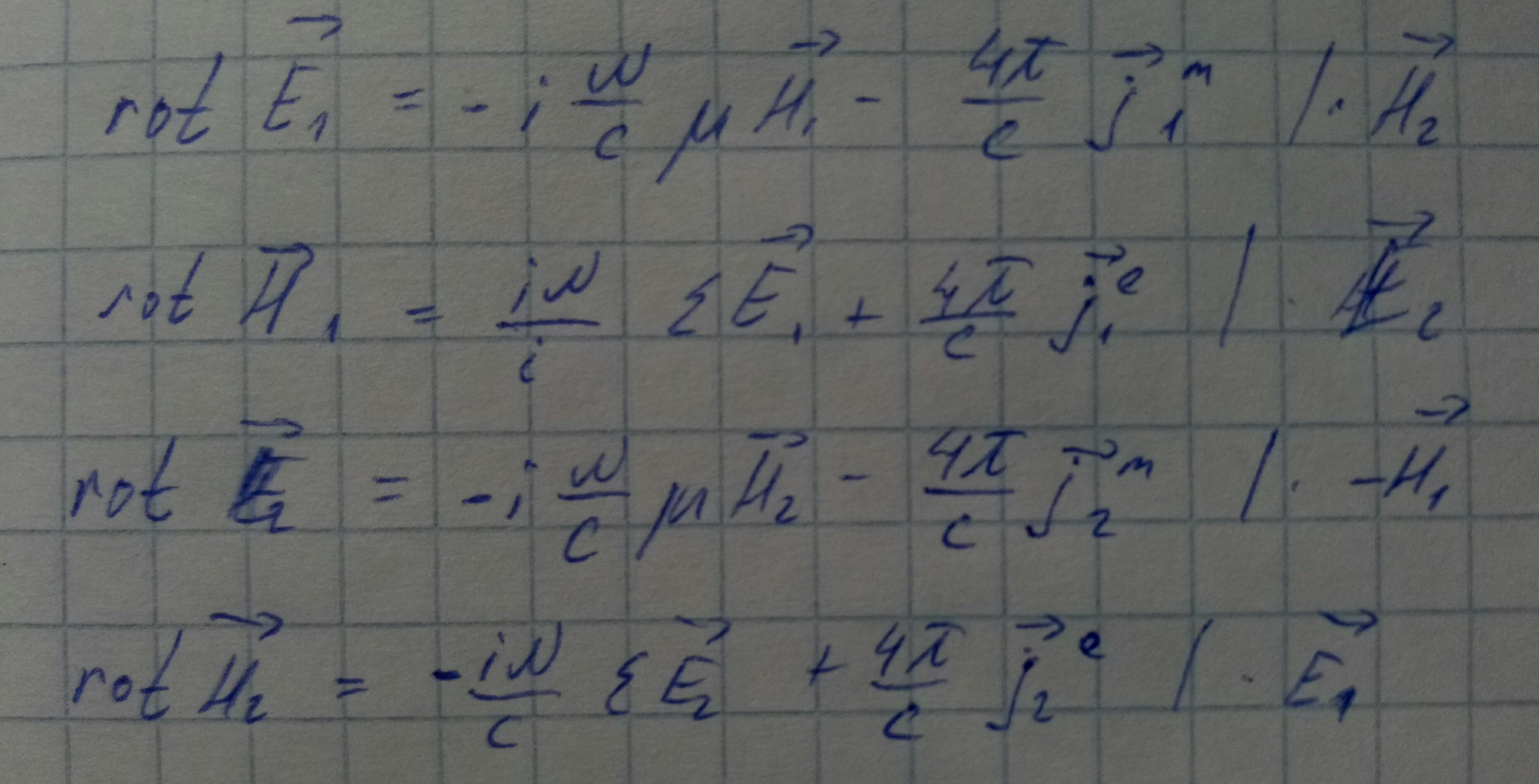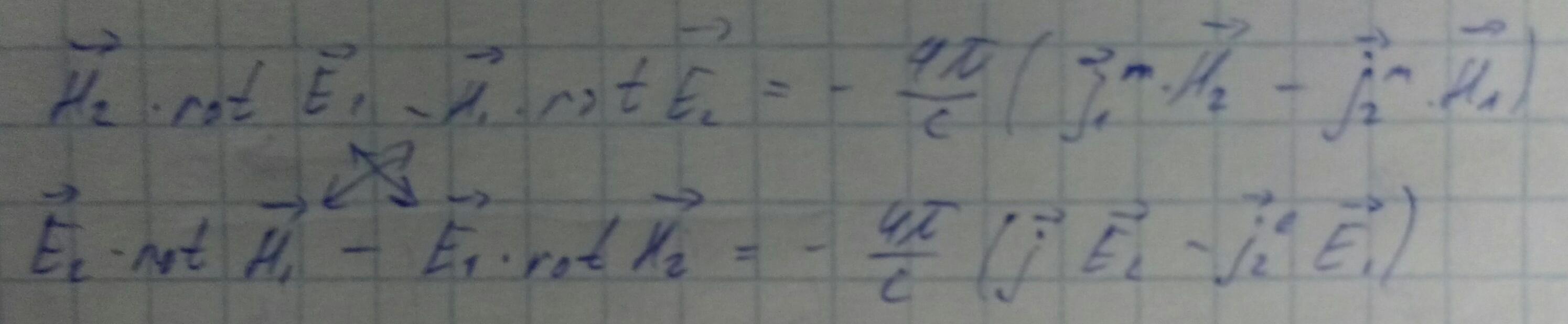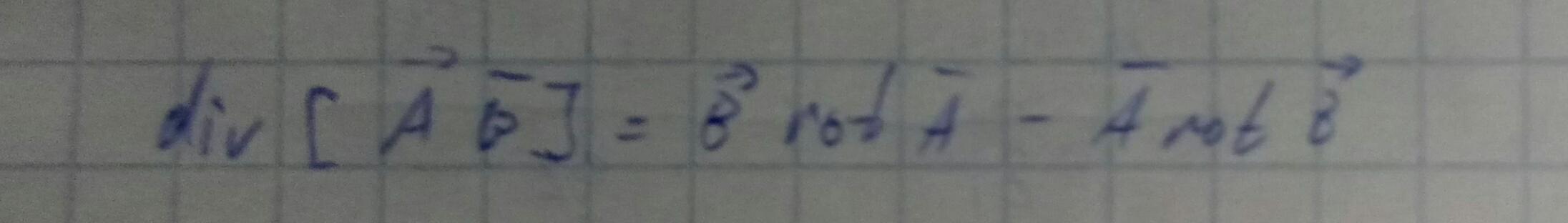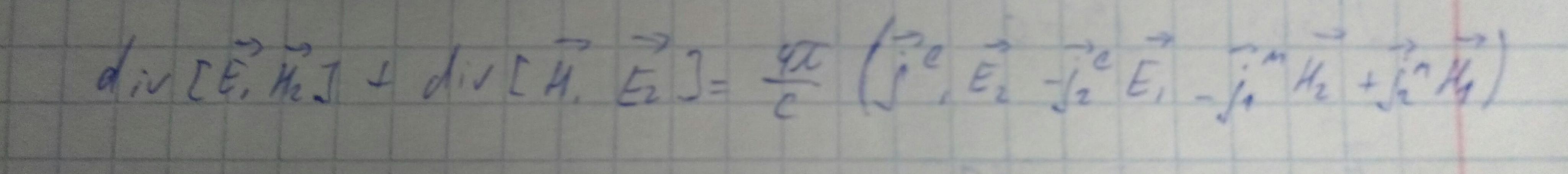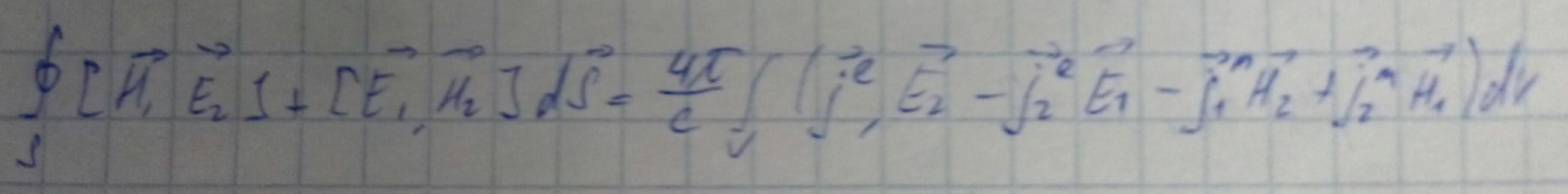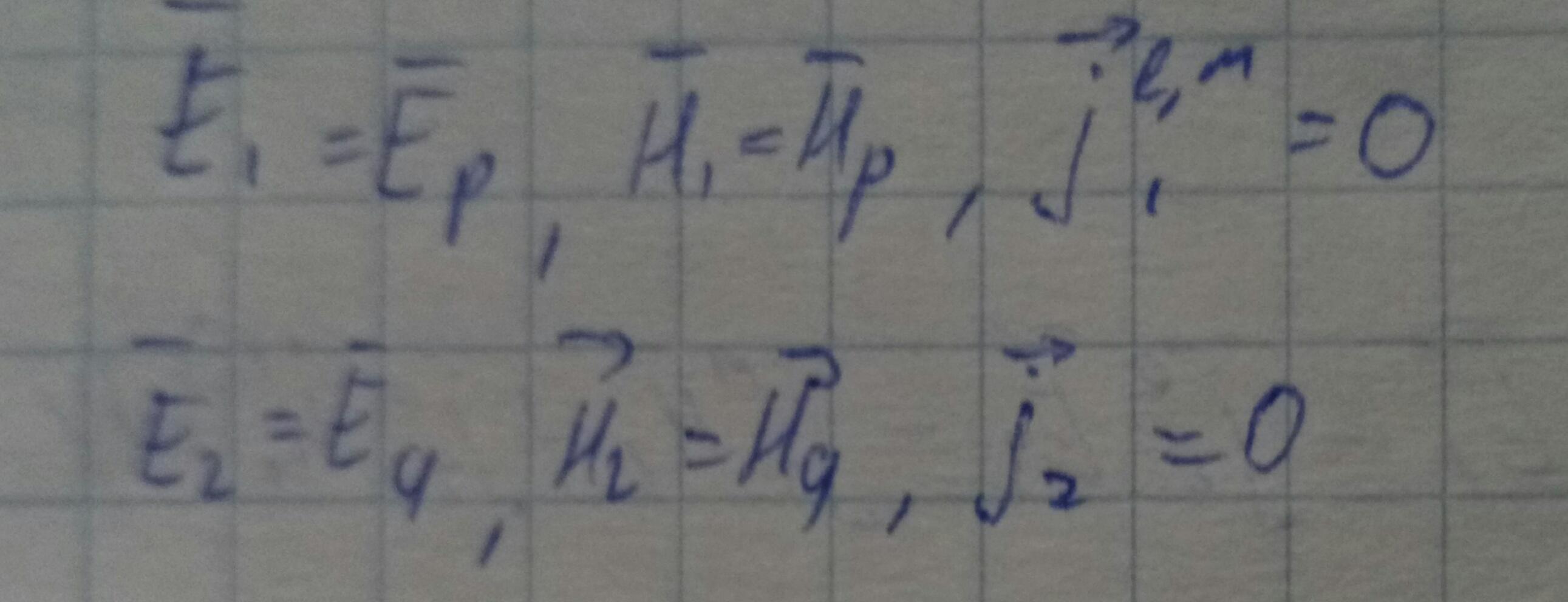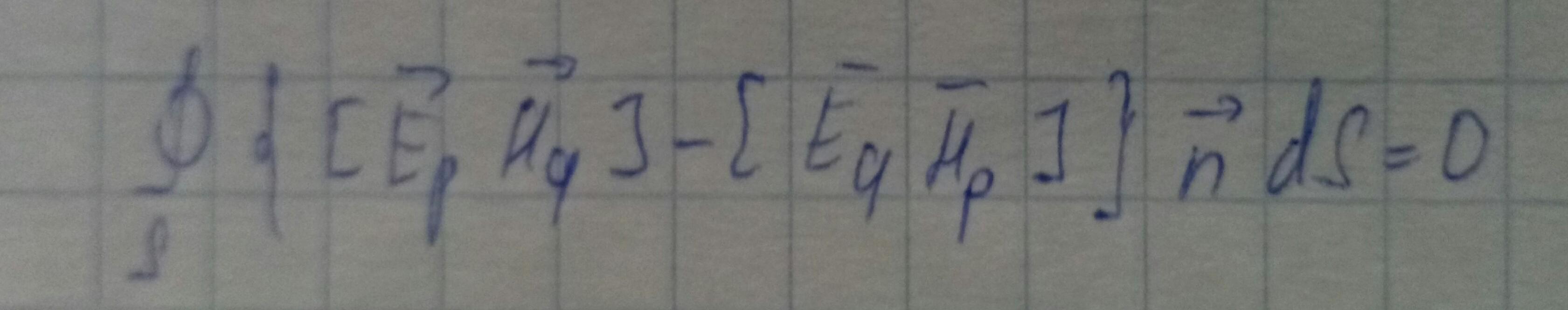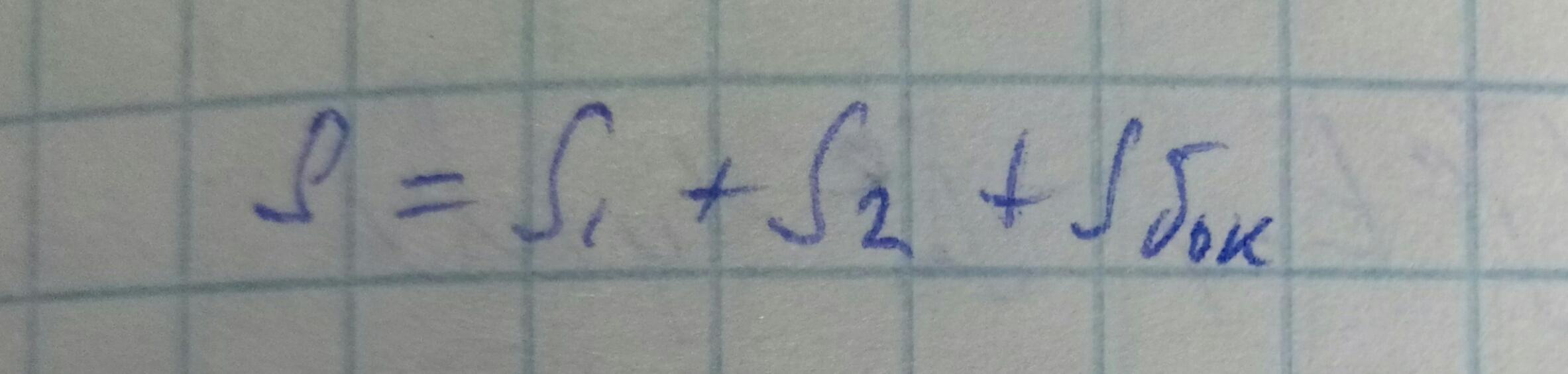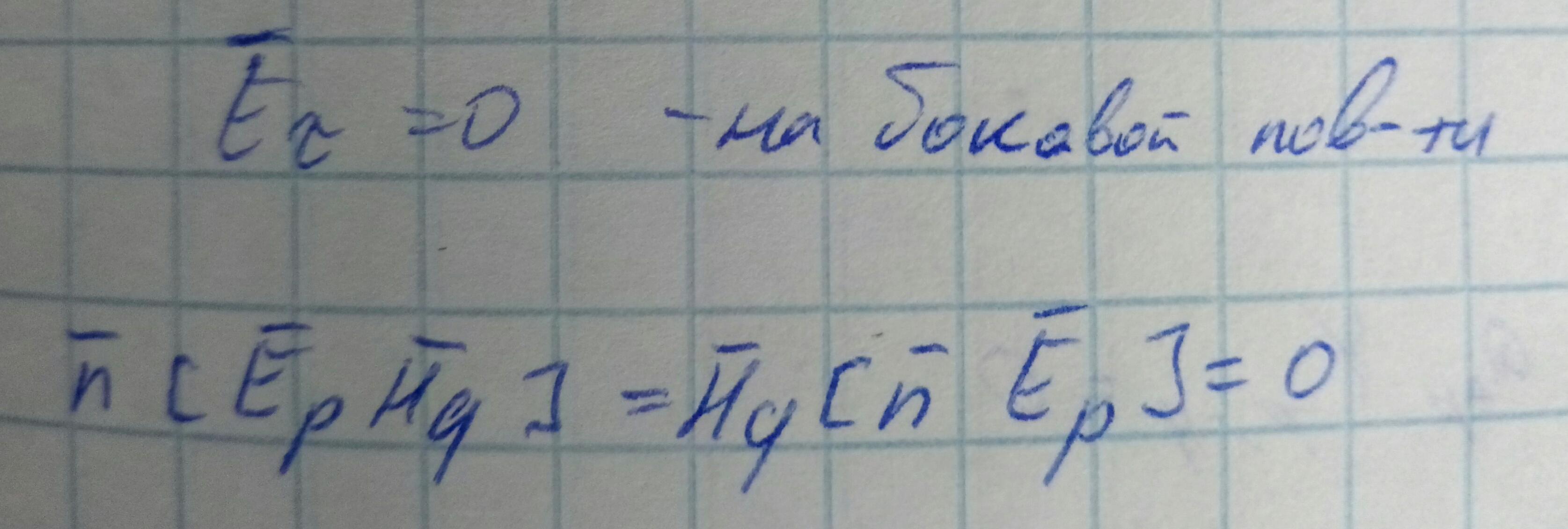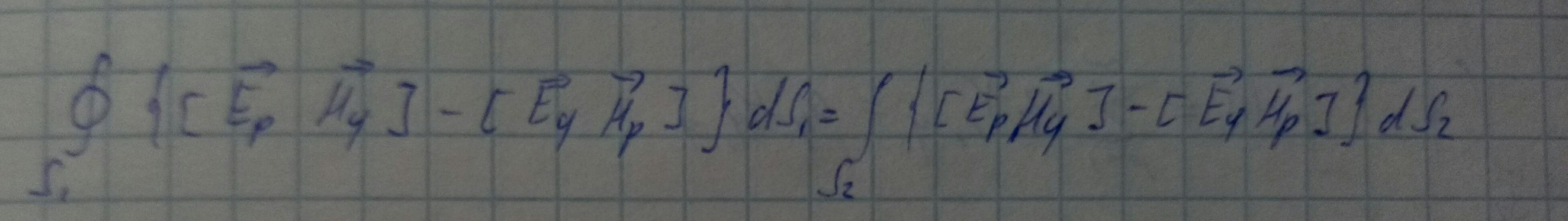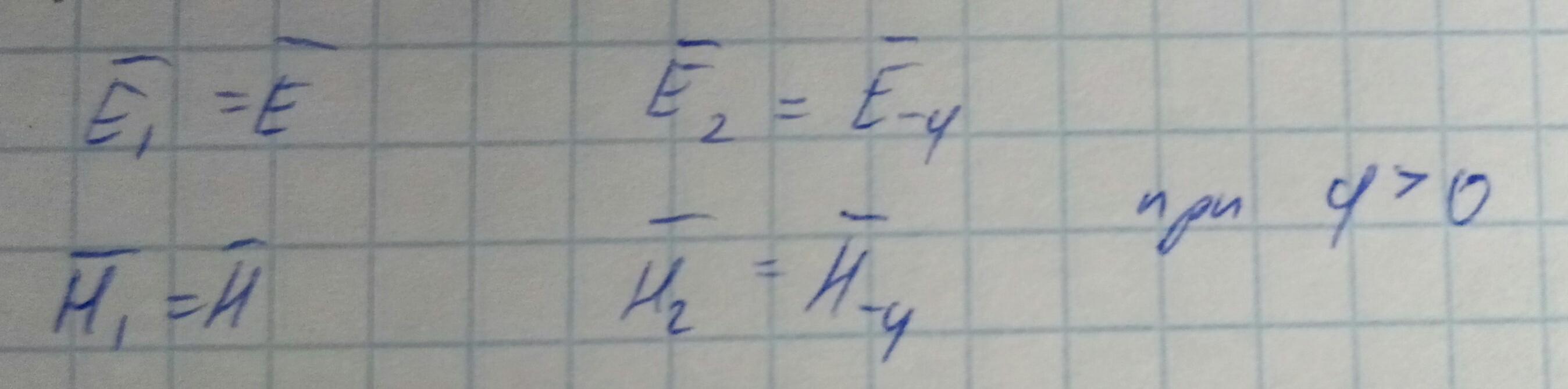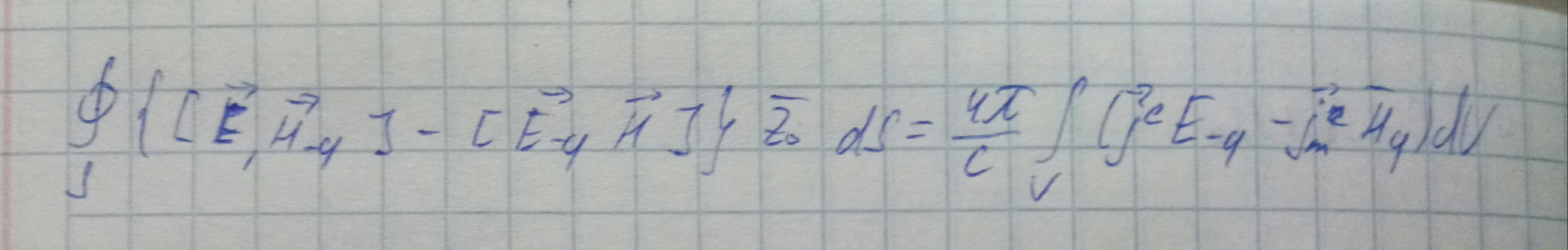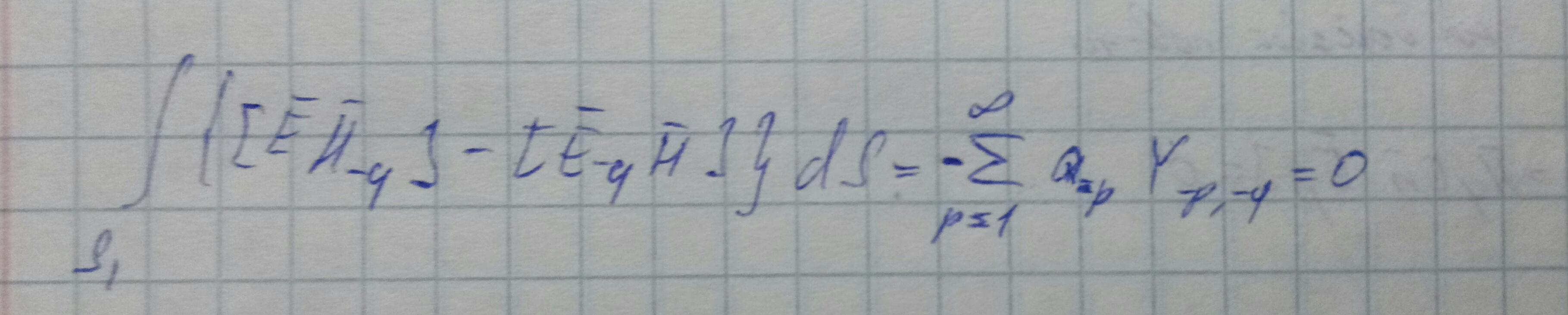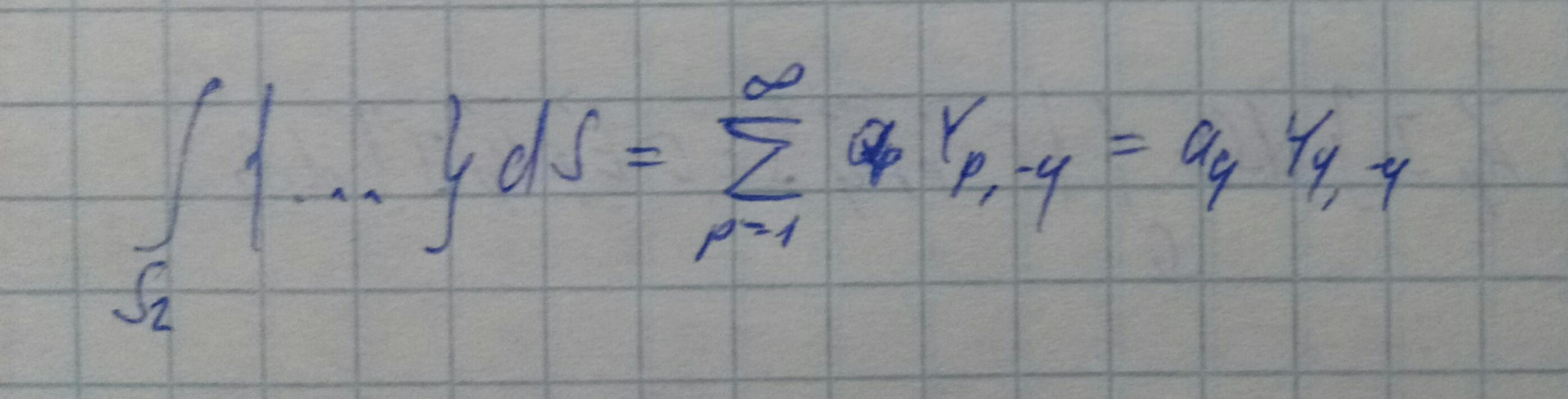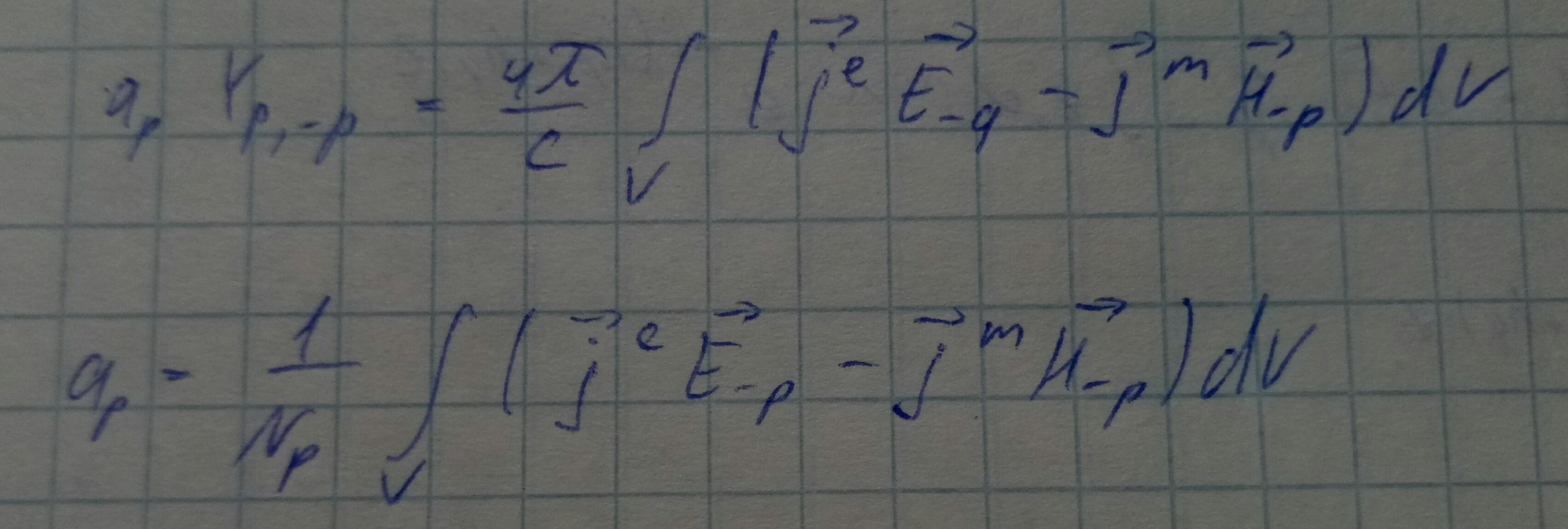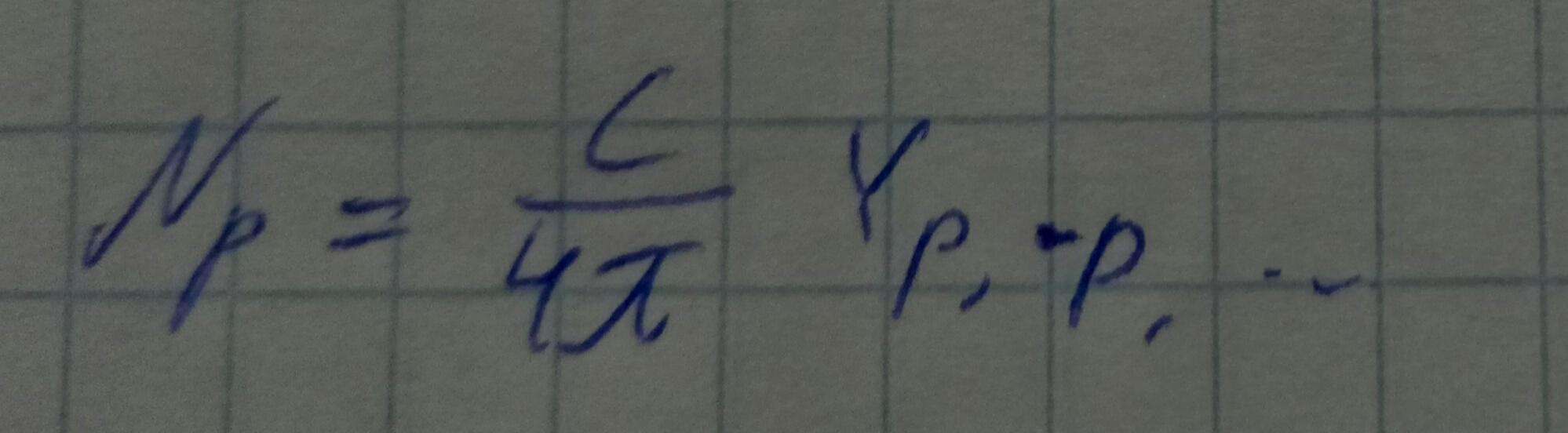Рассмотрим произвольный волновод с идеально проводящими стенками.


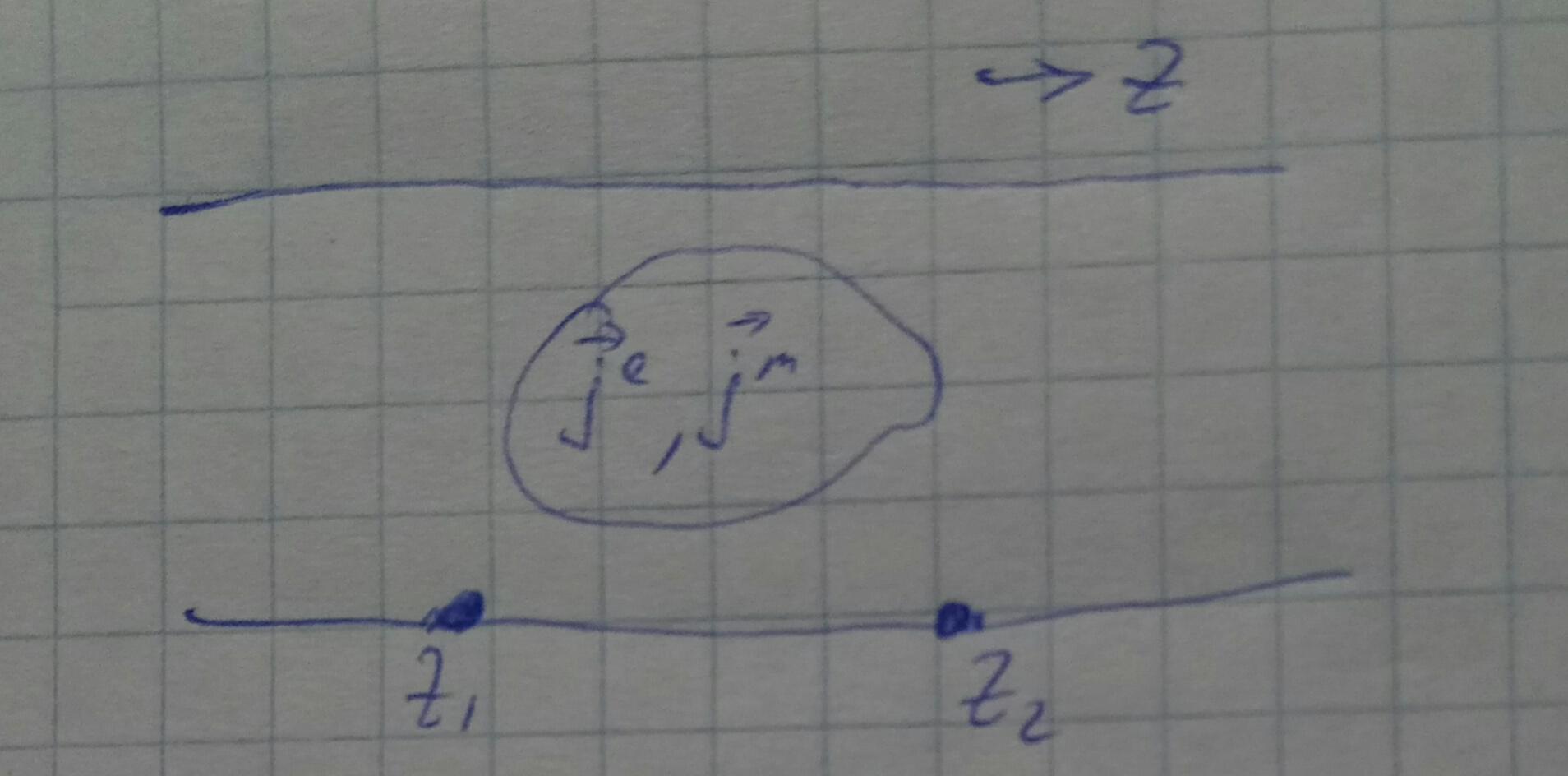
Так как волновод произвольный, обозначим моды через индекс p.


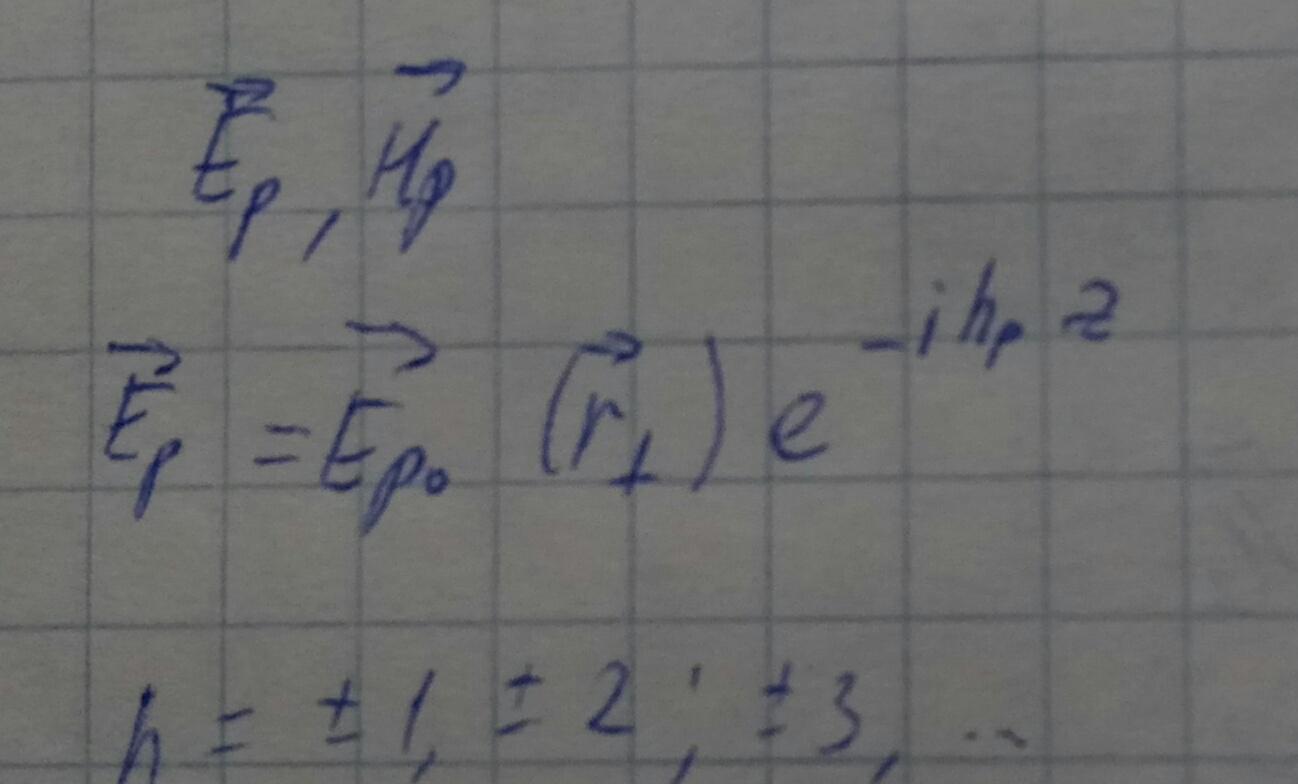
Ep,Hp - напряженности поля собственного колебания с номером p.

Если p>0, то hp>0-мода, бегущая вправо,

Если p<0, то hp<0-мода, бегущая влево.

Разложим поле по собственным модам:

 

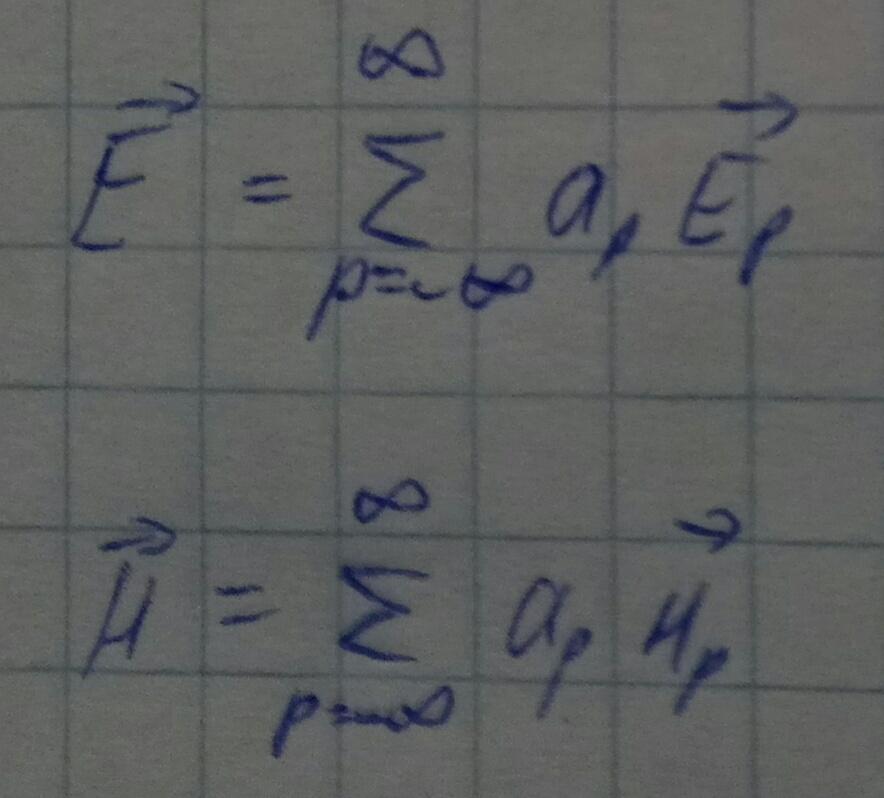
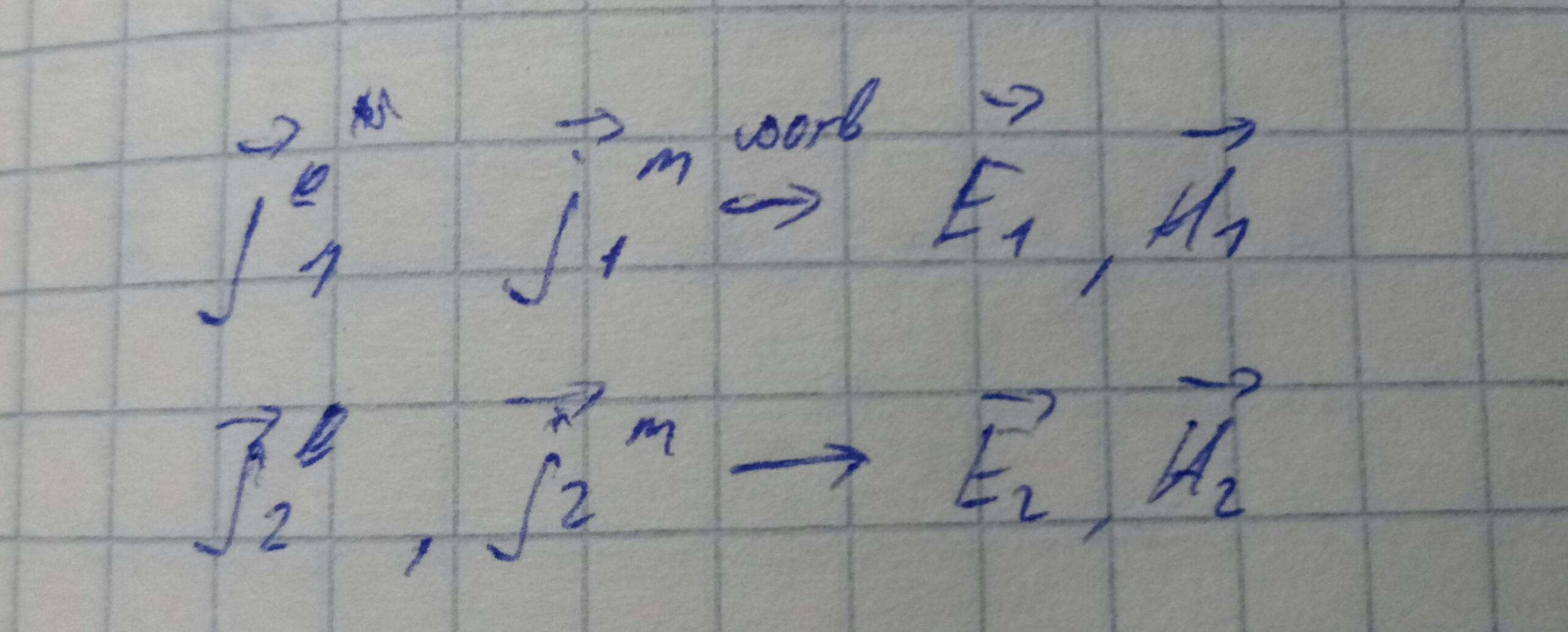
Соотношение ортогональности мод волновода
 
Докажем его с помощью леммы Лоренца. Для этого рассмотрим участок волновода от z1 до z2 и введем сечения произвольной формы S1 и S2. Соответственно получили объем, заключенный между стенками волновода и сечениями S1 и S2. Рассмотрим две моды в данном объеме.



Рассмотрим поля, распространяющиеся в данном объеме и применим к ним лемму Лоренца


где n - нормаль к поверхности. Поверхность состоит из трех составляющих: боковой поверхности и поверхностей S1 и S2.


Граничные условия на боковой поверхности имеют вид:


Интеграл на боковой поверхности равен нулю.


Рассмотрим отдельно интеграл


Этот интеграл не зависит от z в двух случаях:

Полученное соотношение называется соотношением ортогональности мод волновода.

Запишем лемму Лоренца для выделенного обьема V в случае, когда:




Так как тангенсальная составляющая вектора напряженности электрического поля равна нулю, значит данный интеграл по боковой поверхности тоже равен нулю. Рассмотрим интеграл по боковой поверхности S1 и выразим коэффициенты моды через токи в волноводе:




В итоге получаем формулу для нахождения коэффициентов моды через токи в волноводе:

где Np-норма моды(она у моды всегда одна и та же, не зависит от токов):
Оглавление