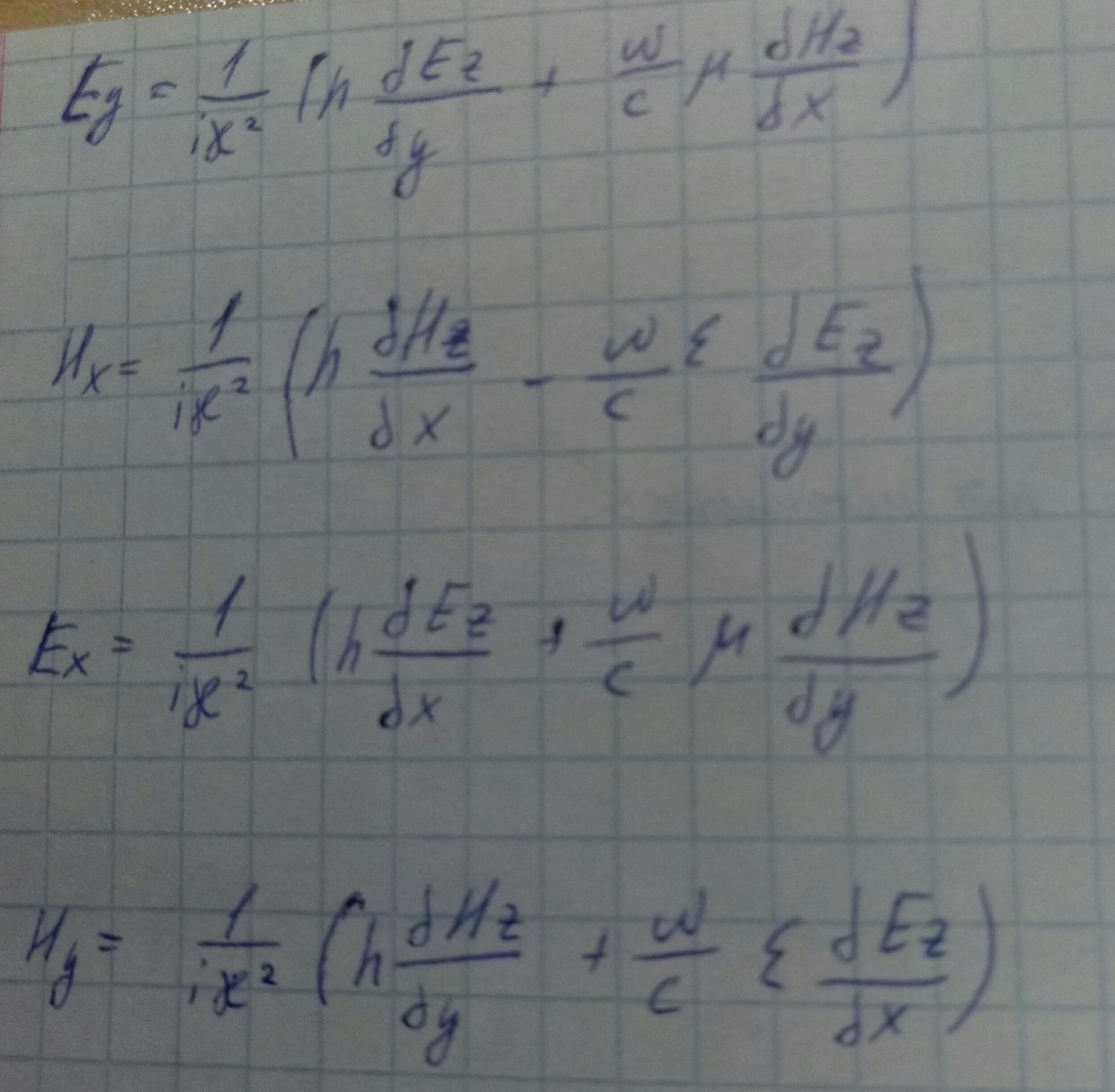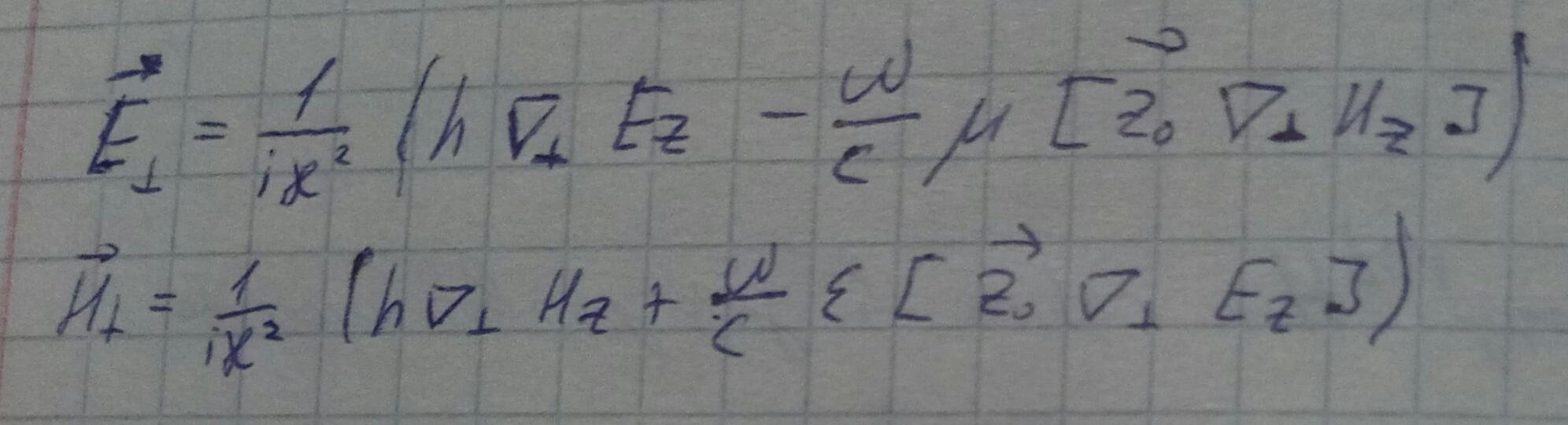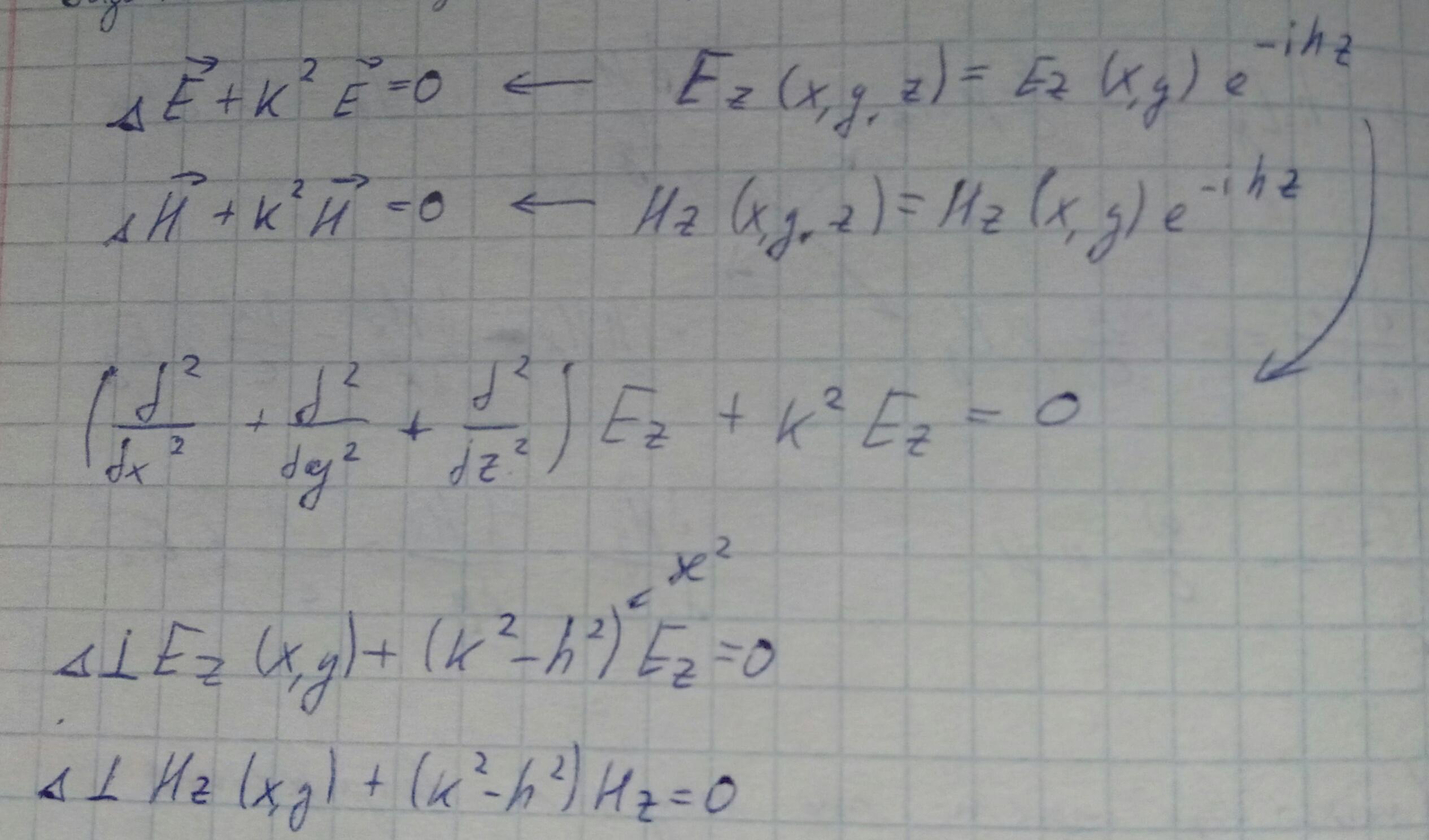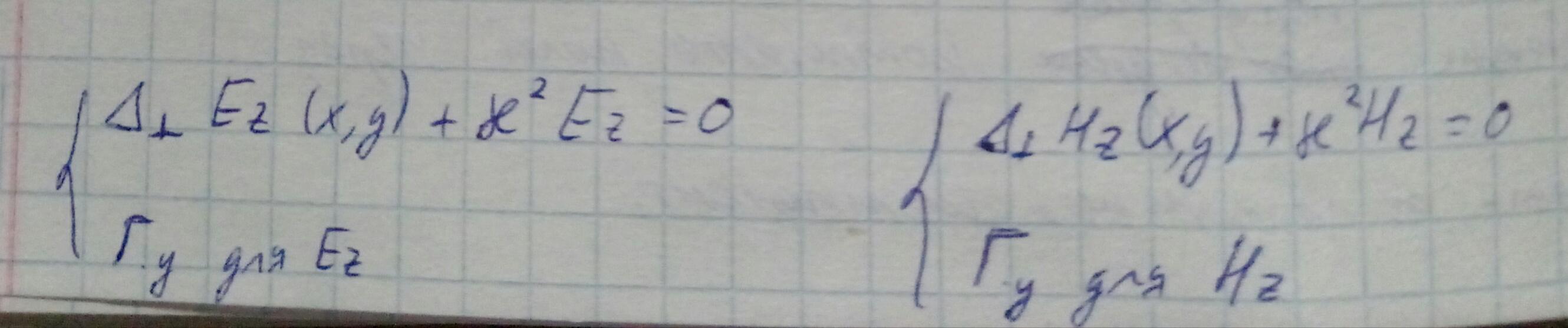Оглавление
Введение
Описание: Понятие волновода, его типы и поперечные компоненты поля.
Задача: передать энергию или информацию из точки А в точку В с помощью электромагнитной волны.

Существует два основных типа передачи информации:
1. Передача без инфраструктуры

В таком случае на вход приемника могут попасть посторонние шумы. Из-за наличия помех уменьшается скорость передачи основного сигнала. Сигналы сторонних источников приводят к снижению чувствительности принимающей антенны. Также возможен перехват информации в точке С.
2.Волноводная передача
Преимущества: энергия не рассеивается, меньше посторонних шумов, сложней прослушать передваемый метериал.
Недостатки: дорого и не мобильно.
| |
Волновод- металло-диэлектрическая конструкция, способная канорировать электромагнитные волны и эффективно передавать их на различные расстояния.
|
Подробная информация о волноводах доступна на сайте Википедия.
Классификация волноводов по степени связи с окружающим пространством:
- Закрытые или экранированные. В них электромагнитное излучение не проникает за стенки волновода.
- Открытые. В них электромагнитное излучение проникает за стенки волновода.
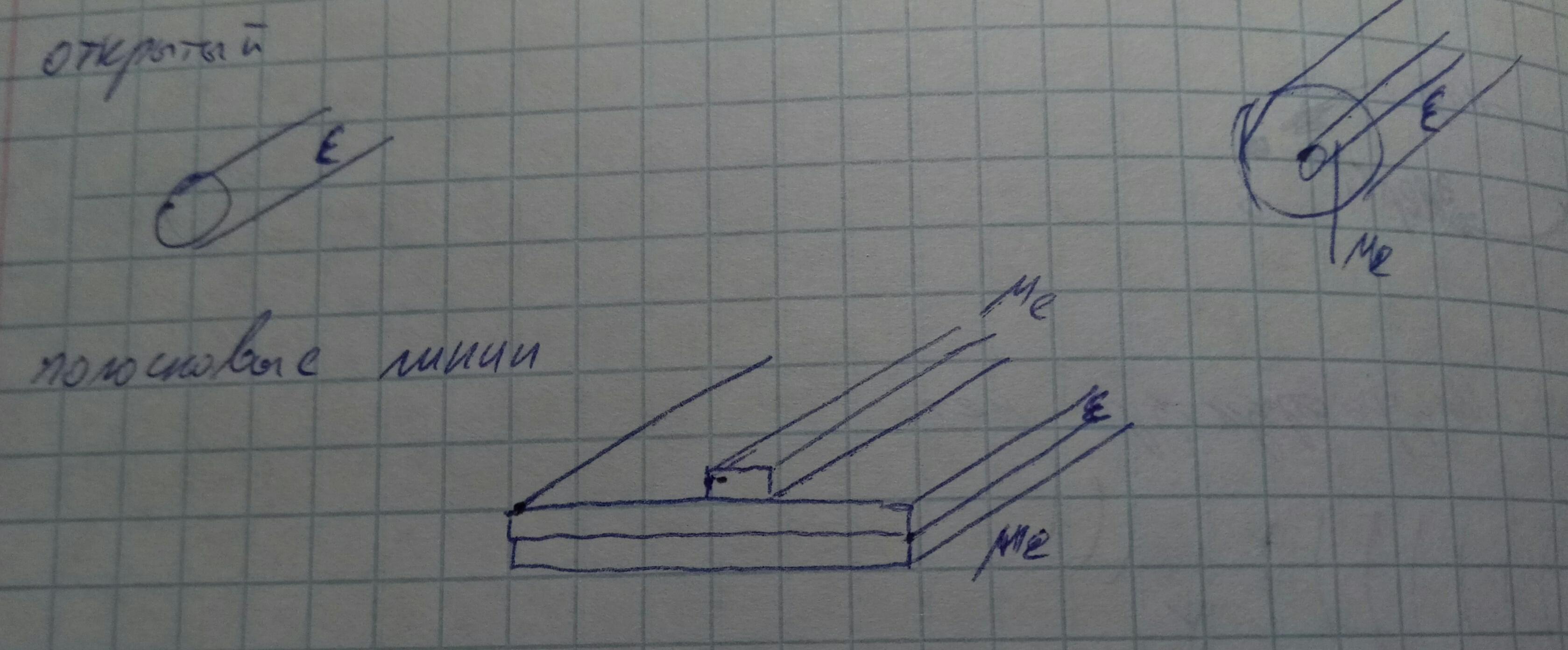
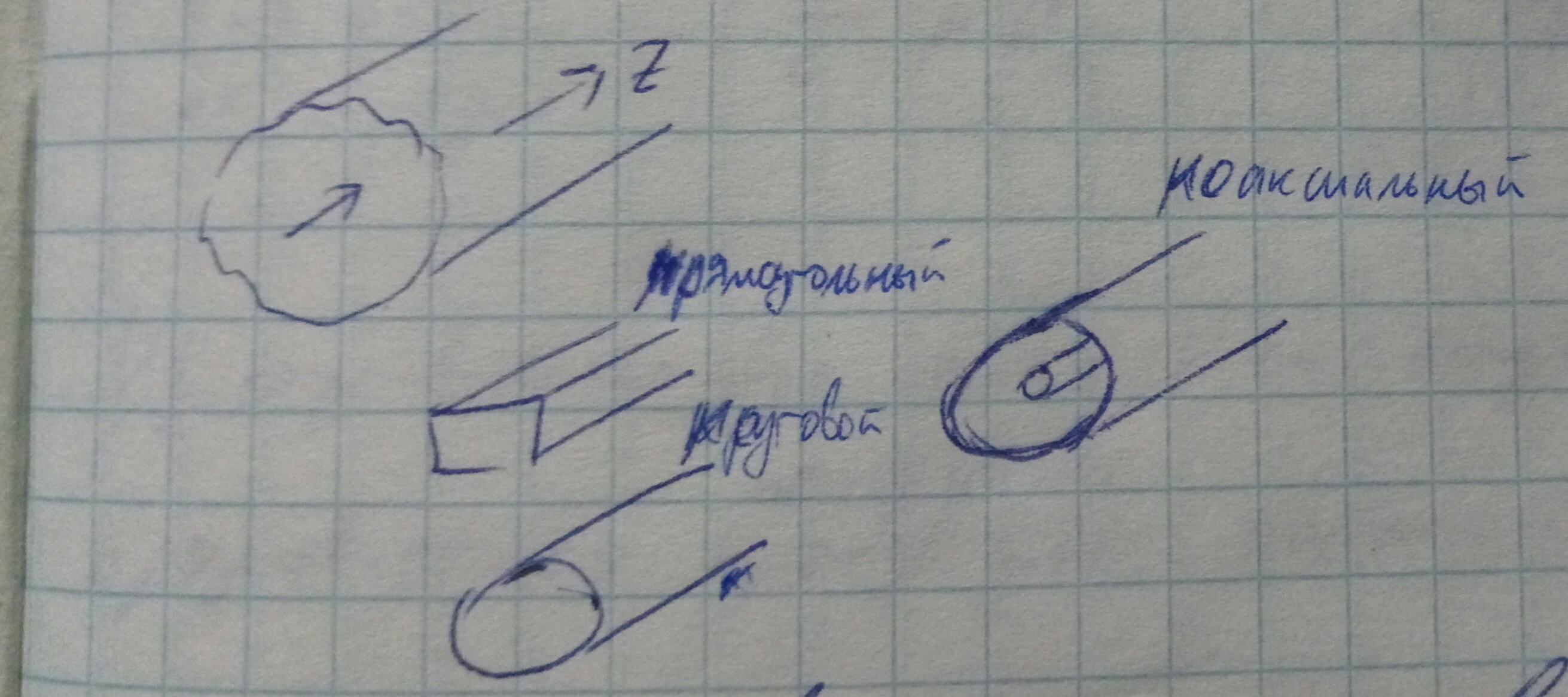
Также волноводы делятся по порядку связности: односвязные( например, прямоугольный), многосвязные( например, коаксиальные), нулевой связности( такое возможно при отсутствии проводящих поверхностей).
По происхождению: естественного и искусственного происхождения.
По зависимости поперечного сечения от продольной координаты: регулярные, нерегулярные, периодические.
Мы будет работать с регулярными волноводами.
| |
Регулярный волновод — волновод, параметры которого не меняются вдоль оси Z.
|
Рассмотрим регулярный волновод, при условии, что в нем нет источников.

И запишем уравнения Максвелла для комплексных амплитуд. Будем ожидать, что в этой структуре распространяется однородная, плоская бегущая волна. Запишем выражения для векторов напряженности электическго и магнитного поля.

Переходя к записи ротора в декартовой системе координат для двух предыдущих уравнений и, группируя соответствующие компоненты, получим следующие выражения:
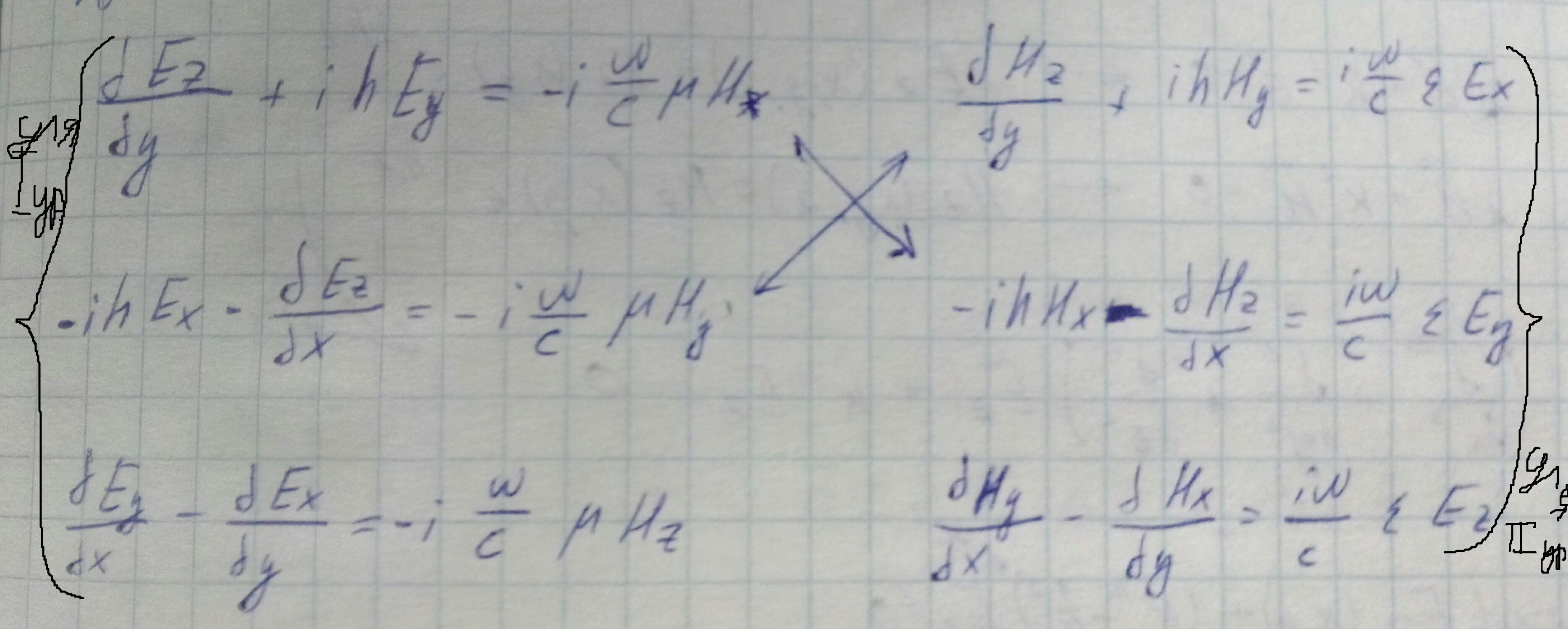
Из данных двух систем получим выражения, представляющие значения поперечных компонент электромагнитного поля через производные от продольных компонент:
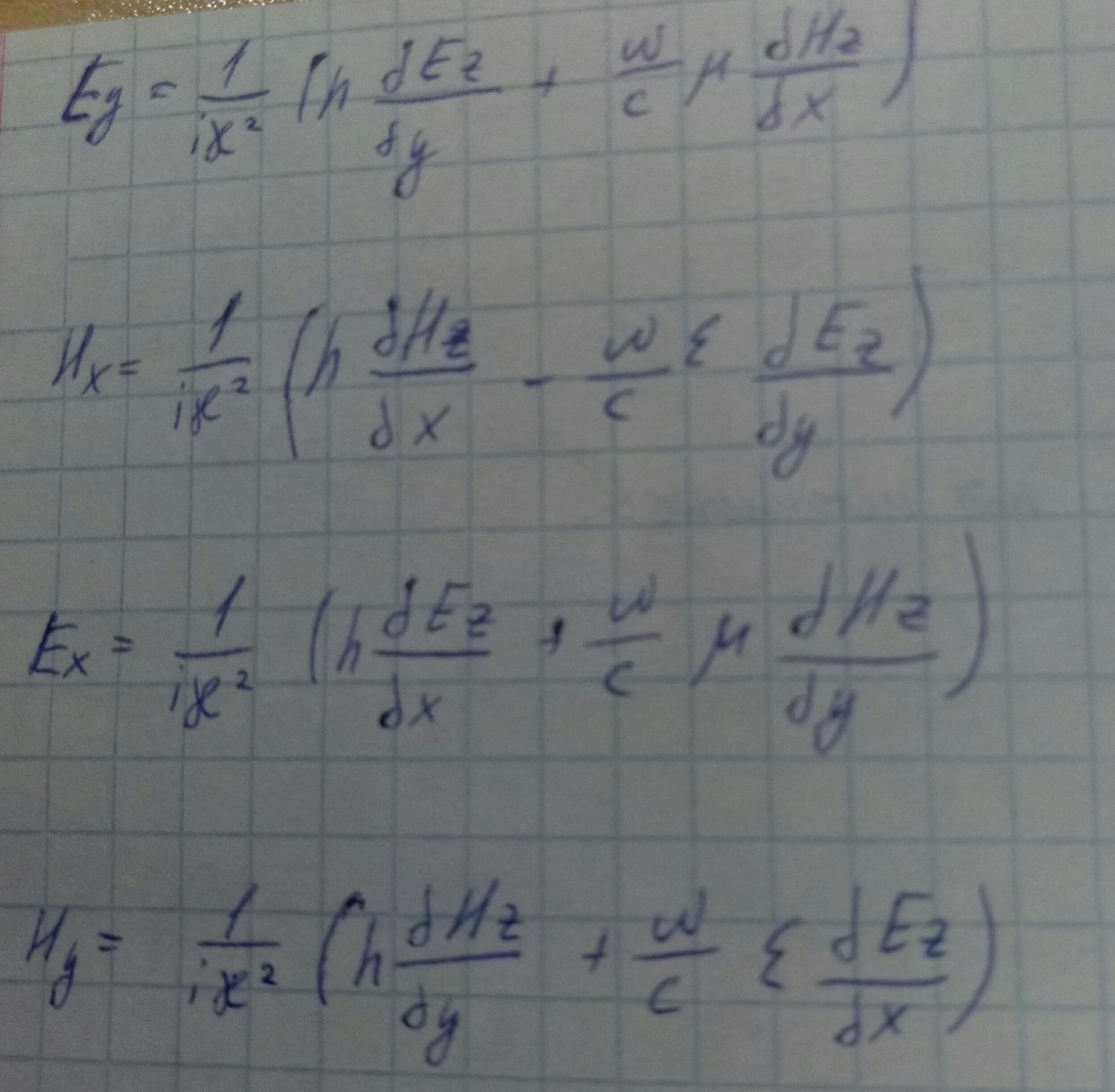
Запишем в векторном виде.
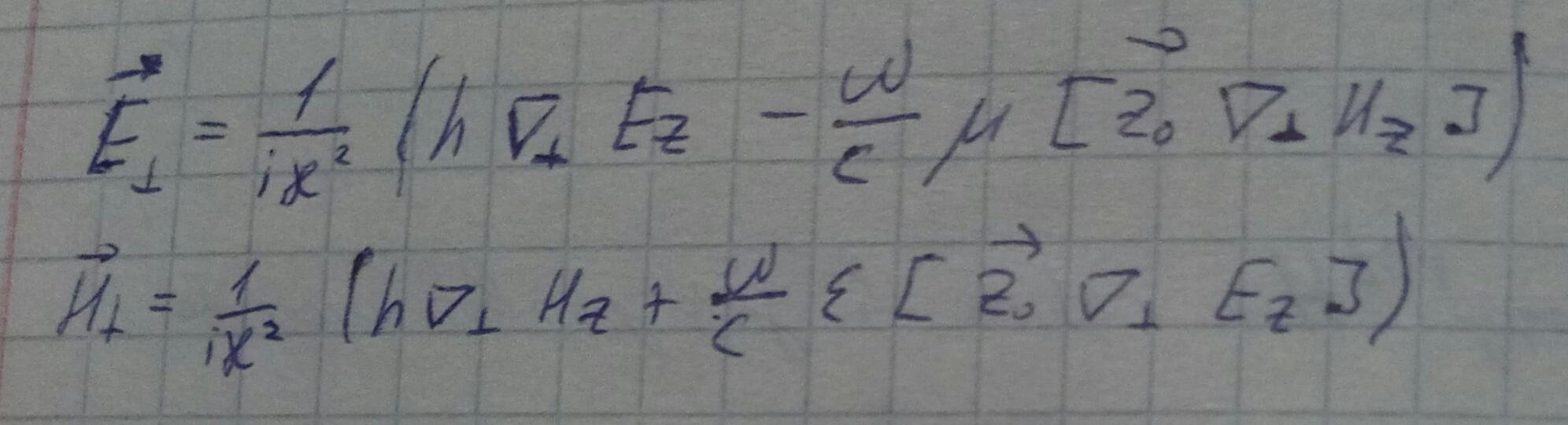
Задача по нахождению продольных компонент Ez и Hz волновода.
Для решения воспользуемся волновым уравнением. Запишем интересующие нас Ez и Hz компоненты, и подставим их в волновые уравнения в результате чего получим уравнение Гемгольца:
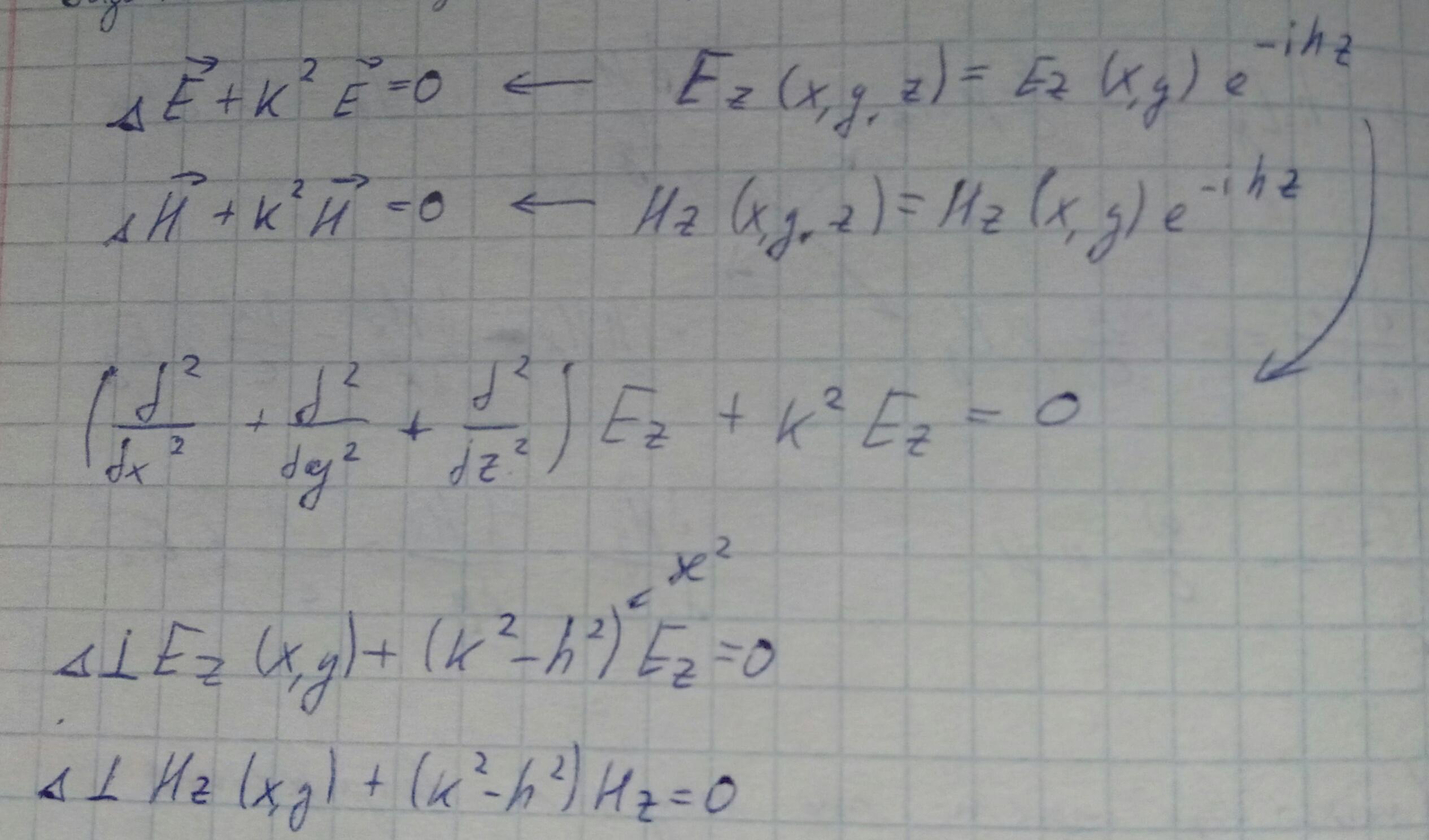
Добавим граничные условия:
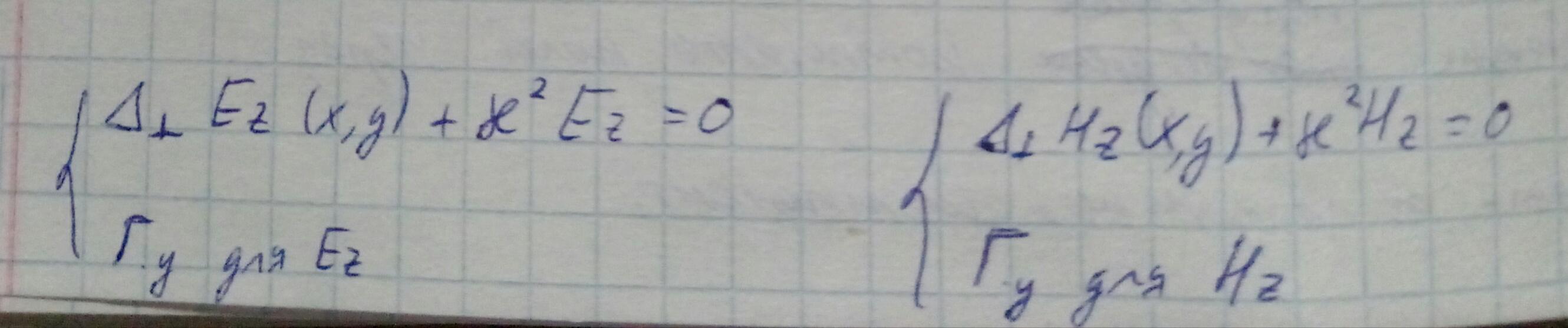
Оглавление