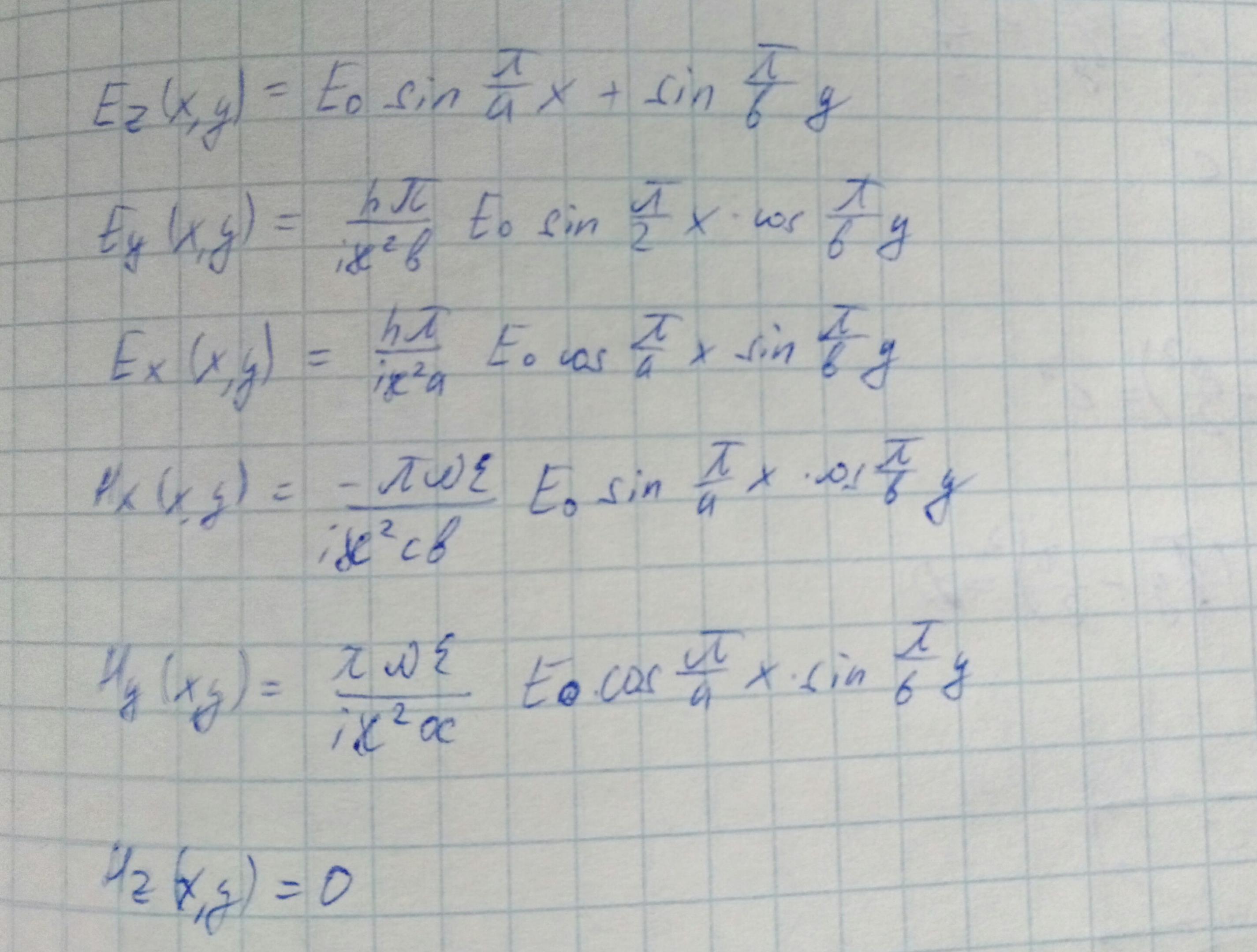
Определяем силовые линии
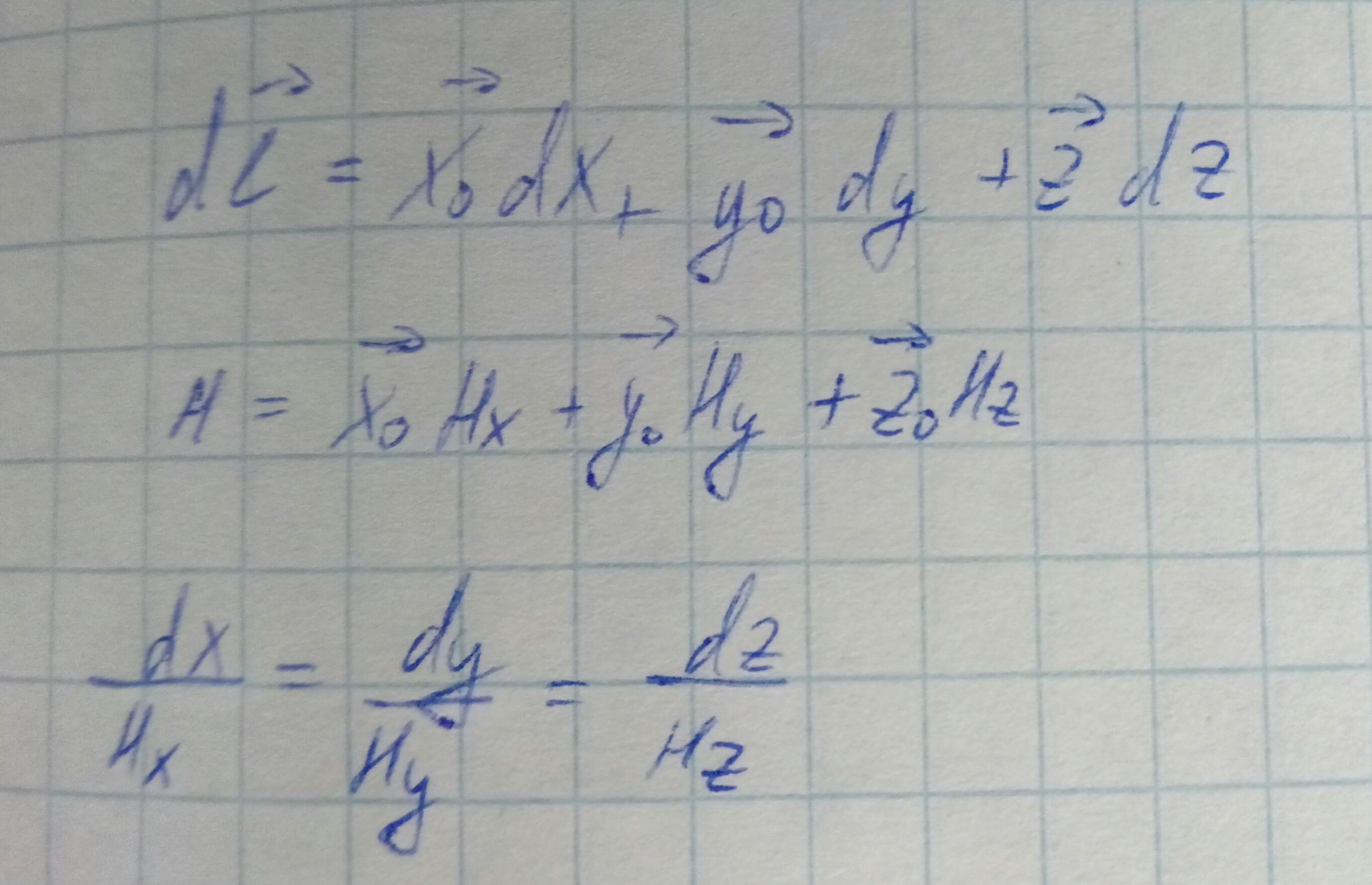
Добавим коэффициенты Ламе, чтобы перейти к криволинейной системе координат.

α и β — малы.
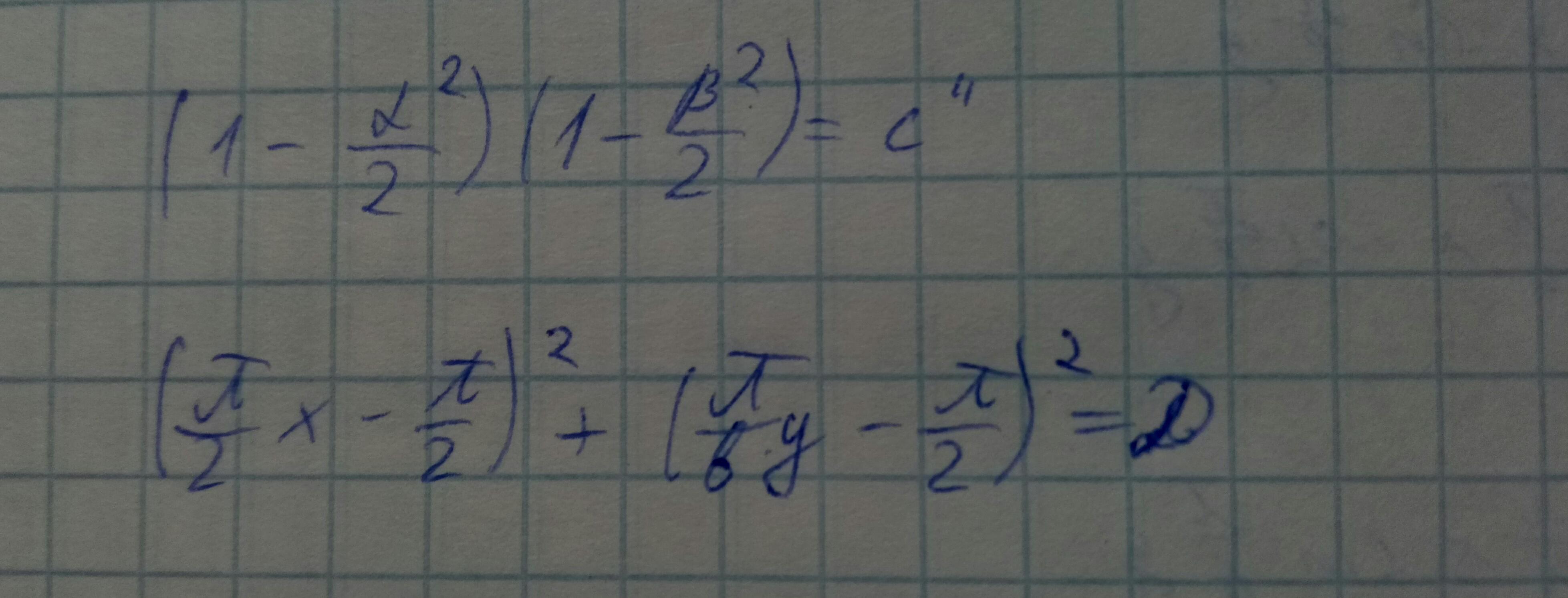
Поперечное сечение.Структура поля H. В пределе похожа на прямоугольник. Линии перпендикулярно втыкаются в стенку.

Построим структуру поля H для моды TM11.
Рассмотрим прямоугольный волновод.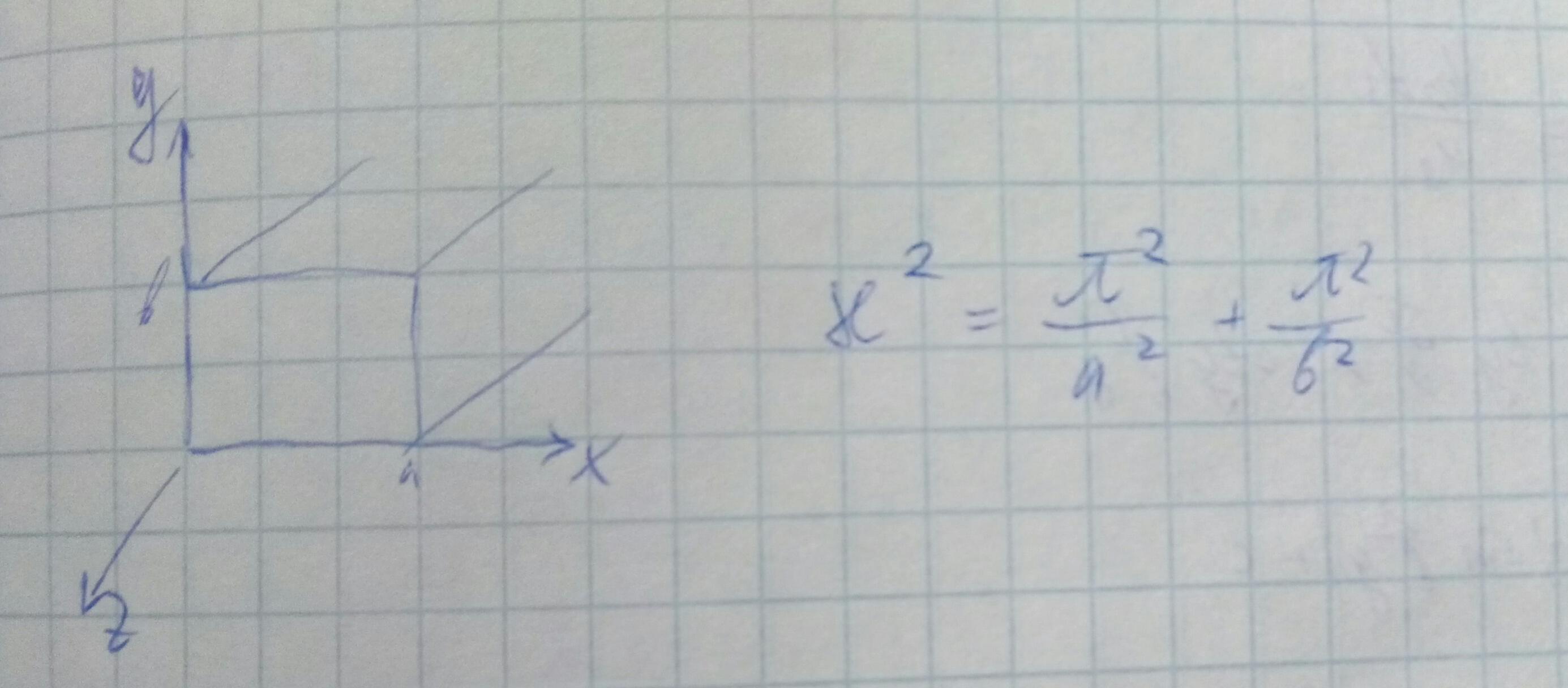
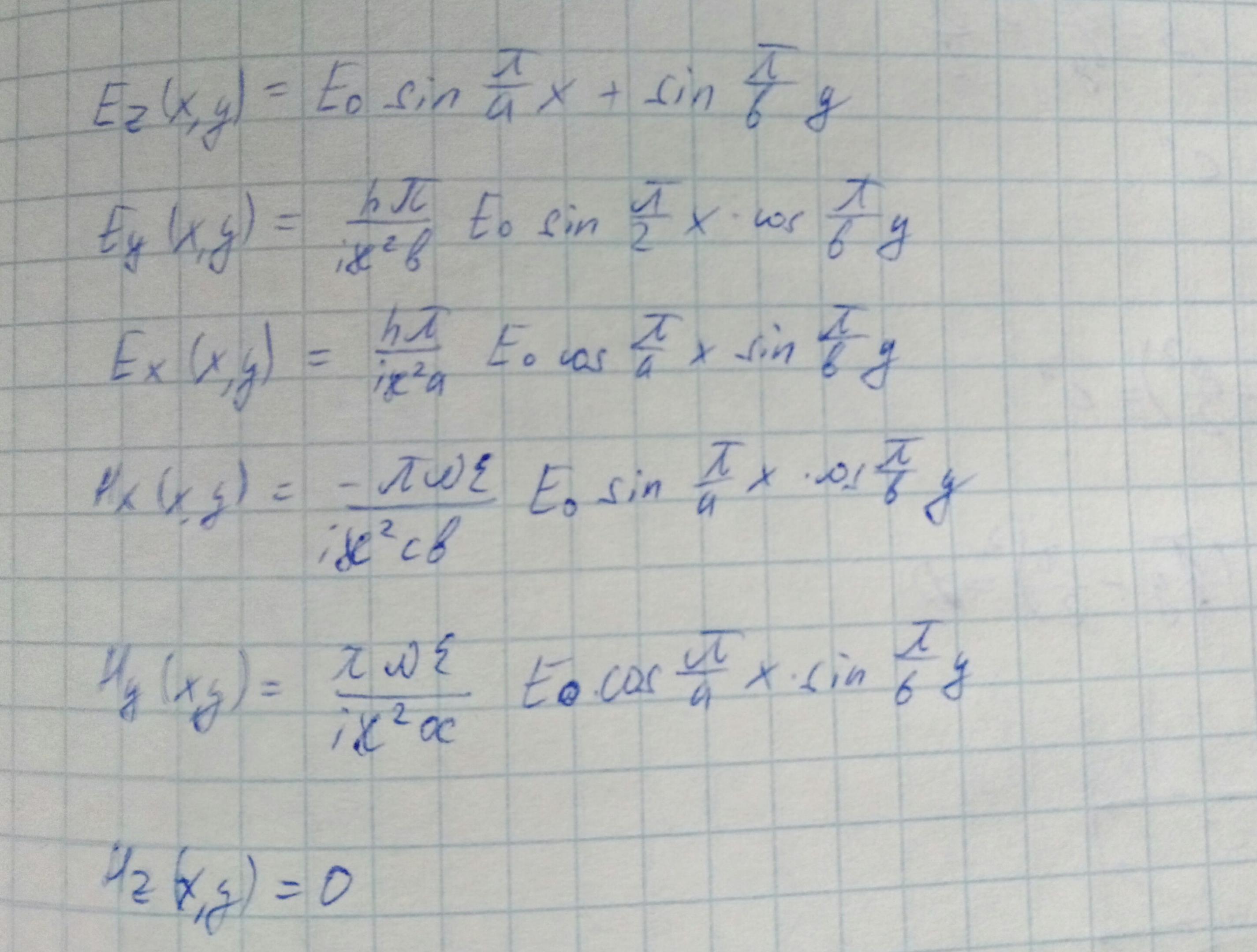
Определяем силовые линии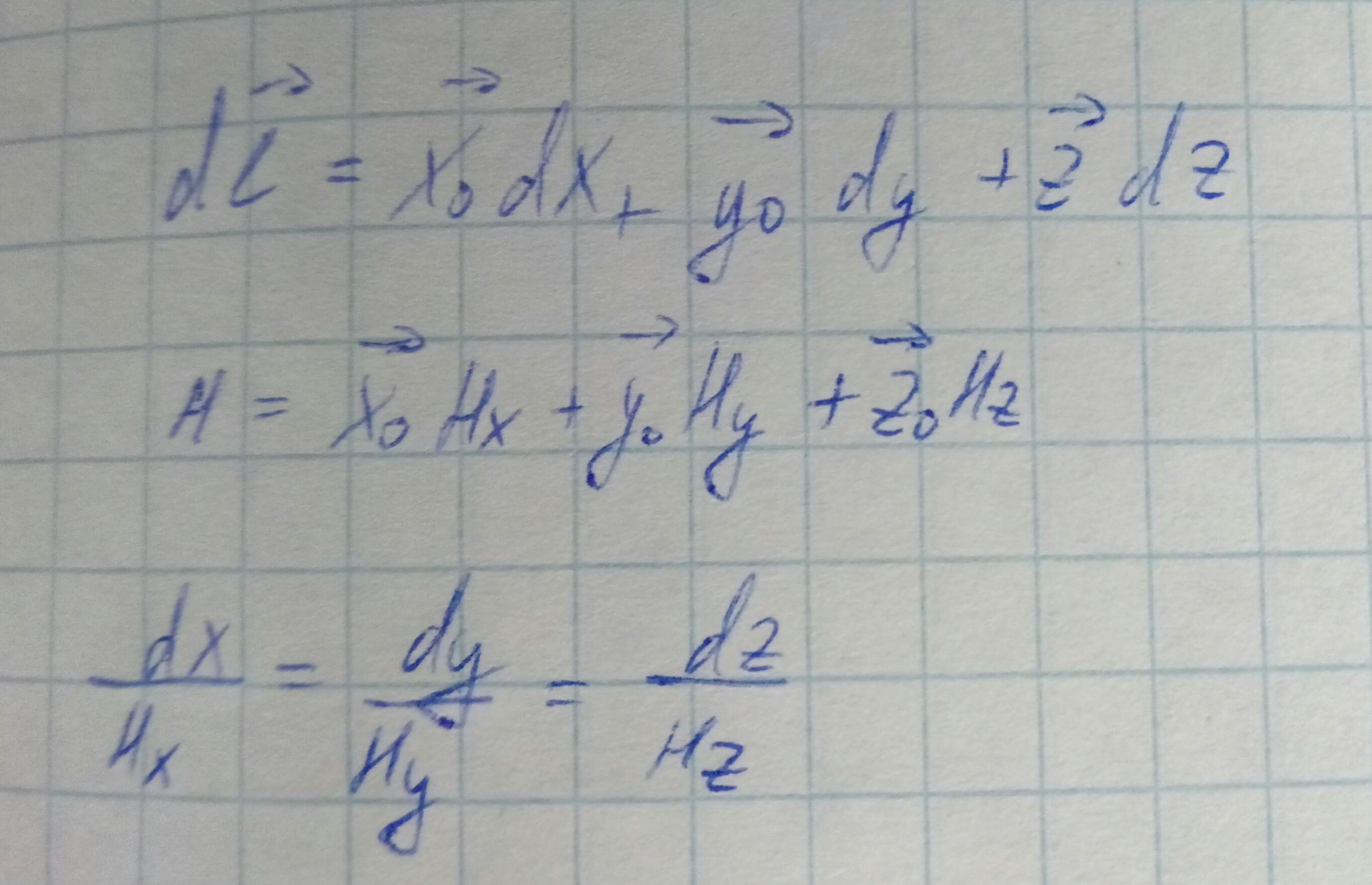
Добавим коэффициенты Ламе, чтобы перейти к криволинейной системе координат.
α и β — малы.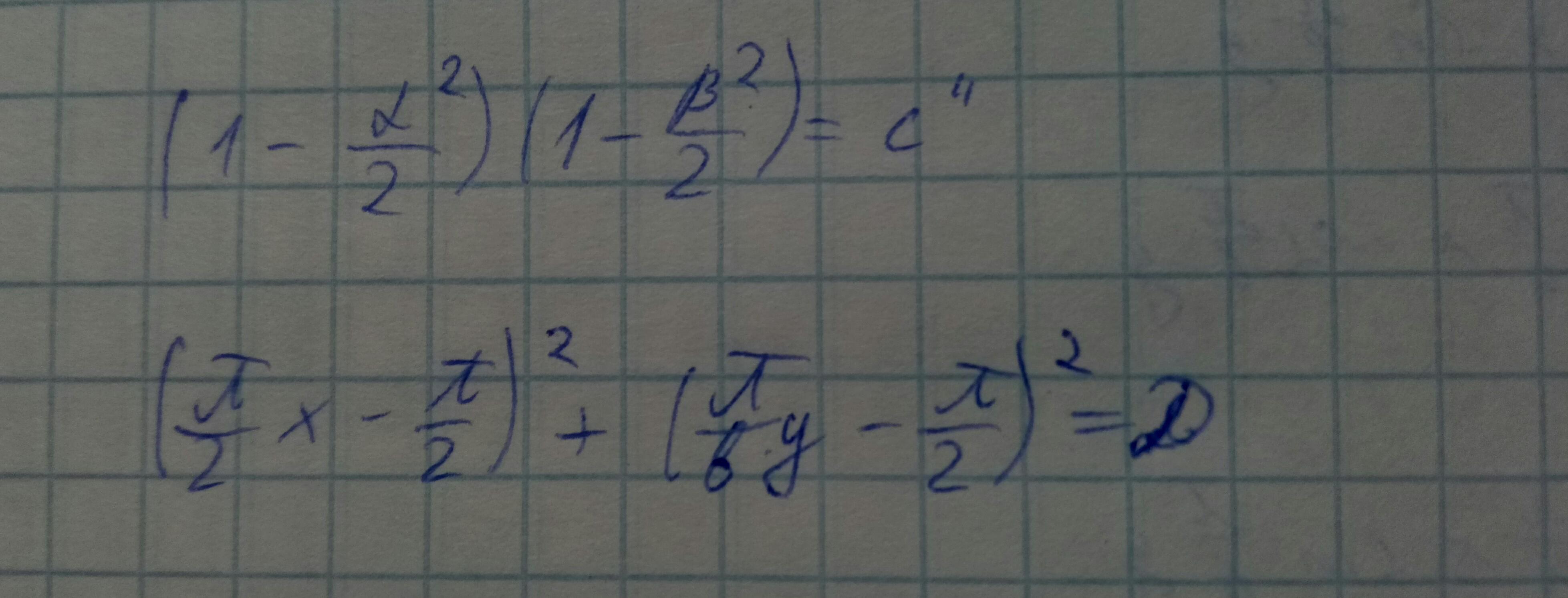
Поперечное сечение.Структура поля H. В пределе похожа на прямоугольник. Линии перпендикулярно втыкаются в стенку.
Затухание волн в волноводе
Волновод линейный, потери не зависят от уровня поля.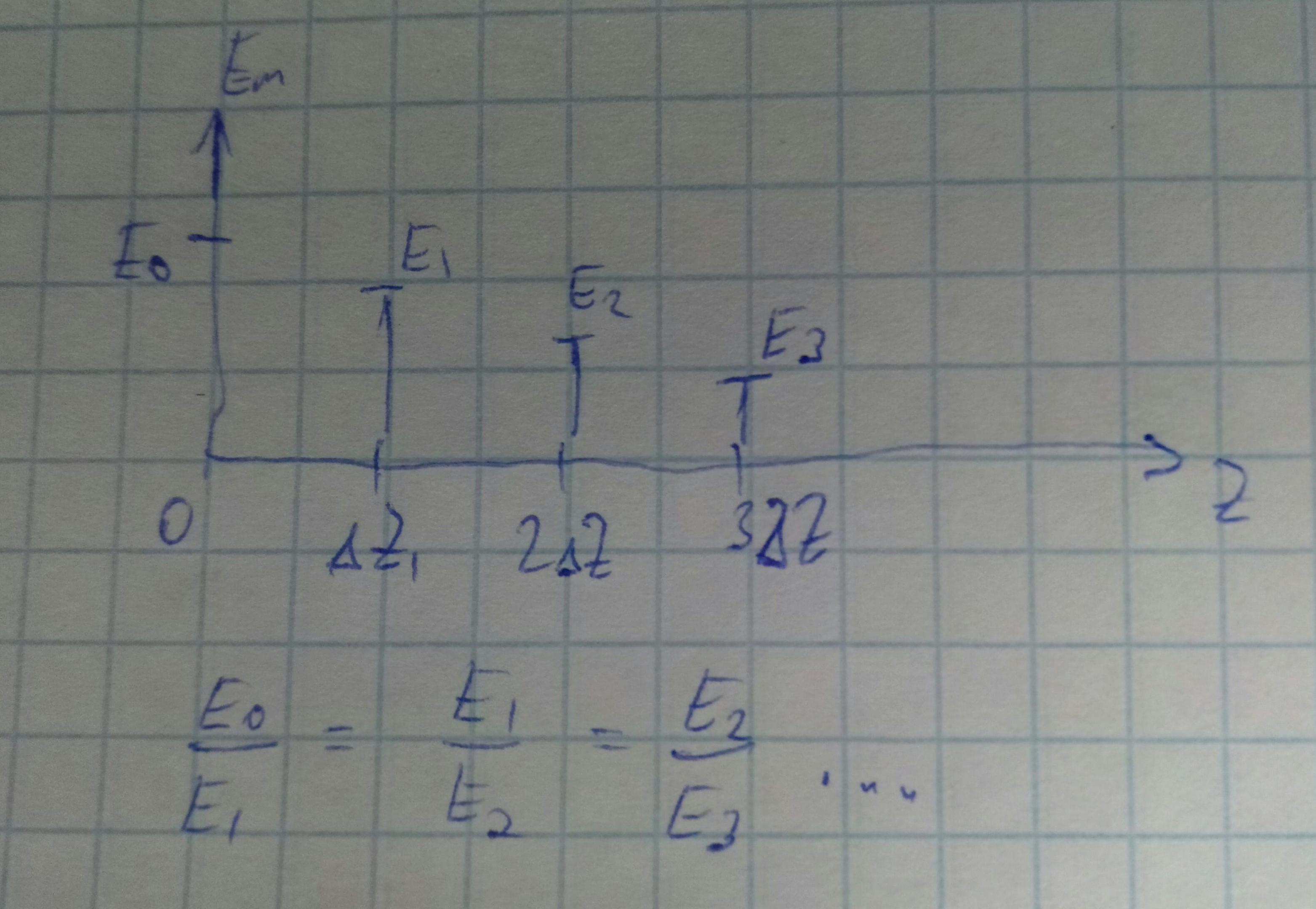
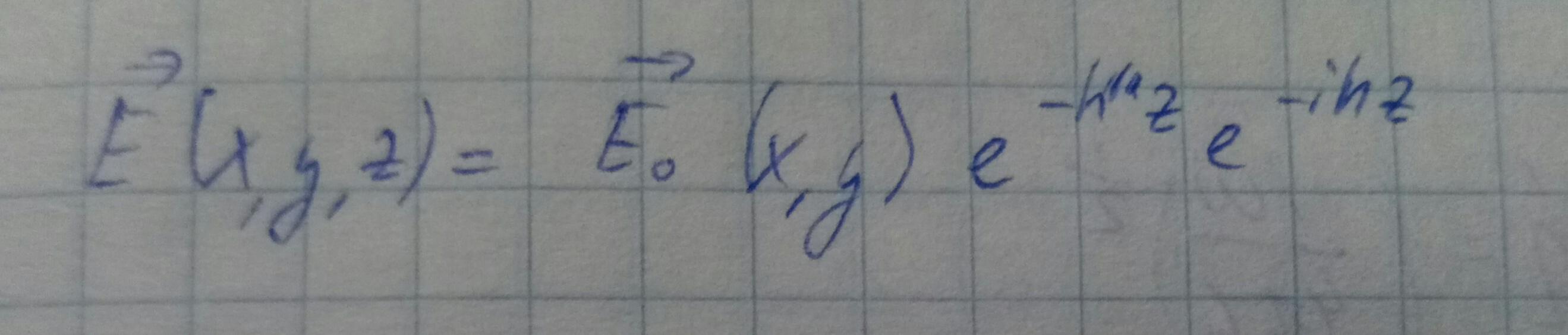
При большой проводимости стенок к волновому числу добавляется малая мнимая часть.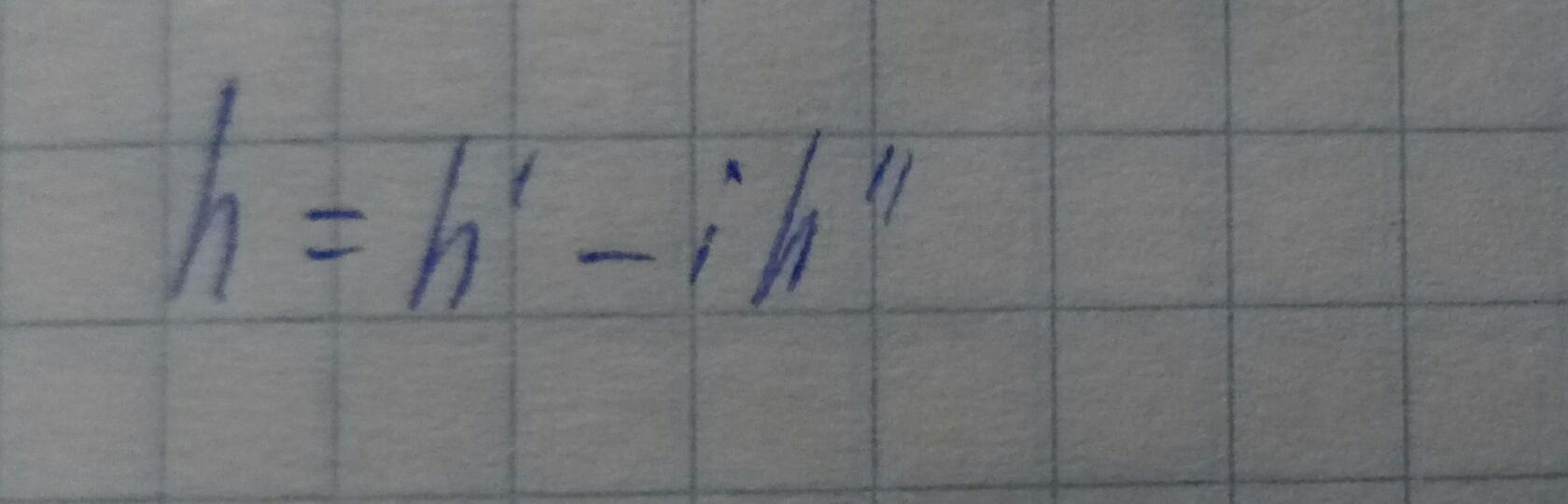
Где h - волновое число для идеально проводящих стенок.
Знак минус здесь обусловлен тем, что происходит спад при увеличении z.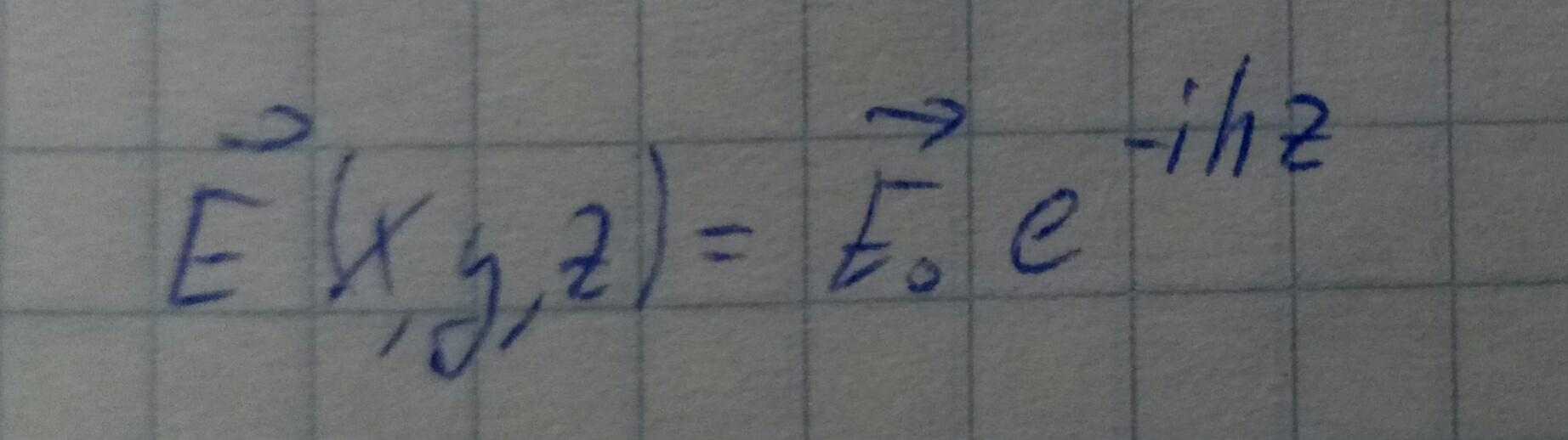
Постоянную затухания можно определить, либо решая заново задачу с граничными условиями, учитывающими конечную проводимость, либо рассчитывая омические потери. (Джексон Дж. Классическая электродинамика., Гл. 8)
Вычислим декремент затухания, свяжим его с потерями, а также рассмотрим потери в стенках волновода.
Будем считать, что потери в волноводе маленькие и структура полей мод в волноводе с потерями такая же как в волноводе без потерь (в нулевом приближении).
P считаем таким же, как в волноводе без потерь.
Граничное условие Леонтовича позволяет на поверхности хорошего проводника находить тангенциальную компоненту поля Е по тангенциальной компоненте Н. Последнюю берем как в волноводе без потерь. Граничное условие Леонтовича: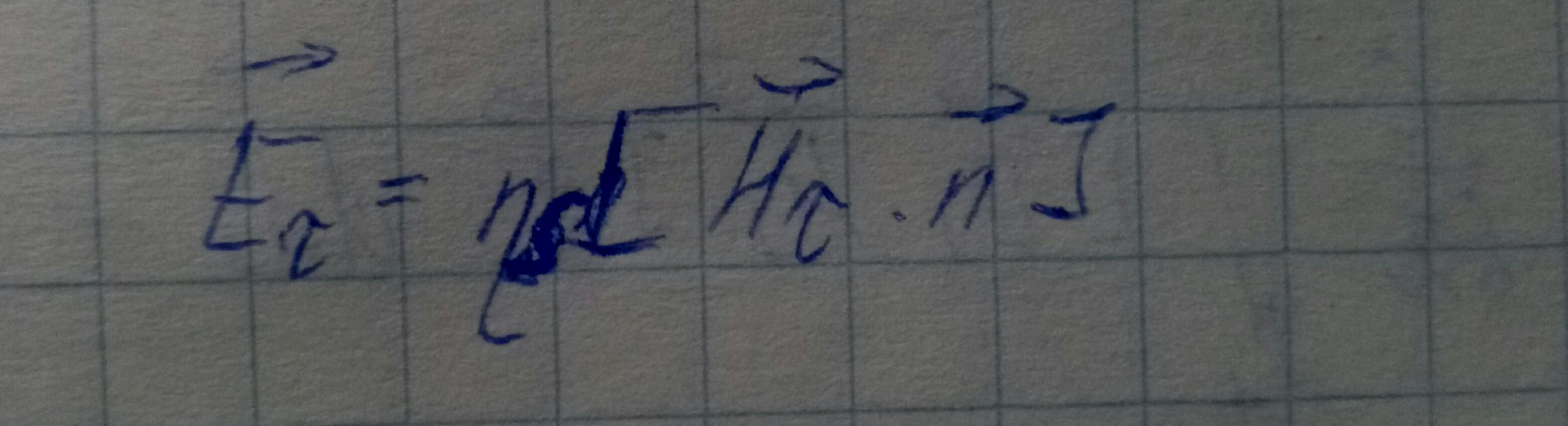

Теперь найдем h'' для моды типа ТЕ10 в волноводе axb в случае:
1) Если одна из широких стенок не идеально проводящая;
2) Одна из узких.
(скриншот из книги "Л.Д.Ландау, Е.М.Лифшиц "Электродинамика сплошных сред").