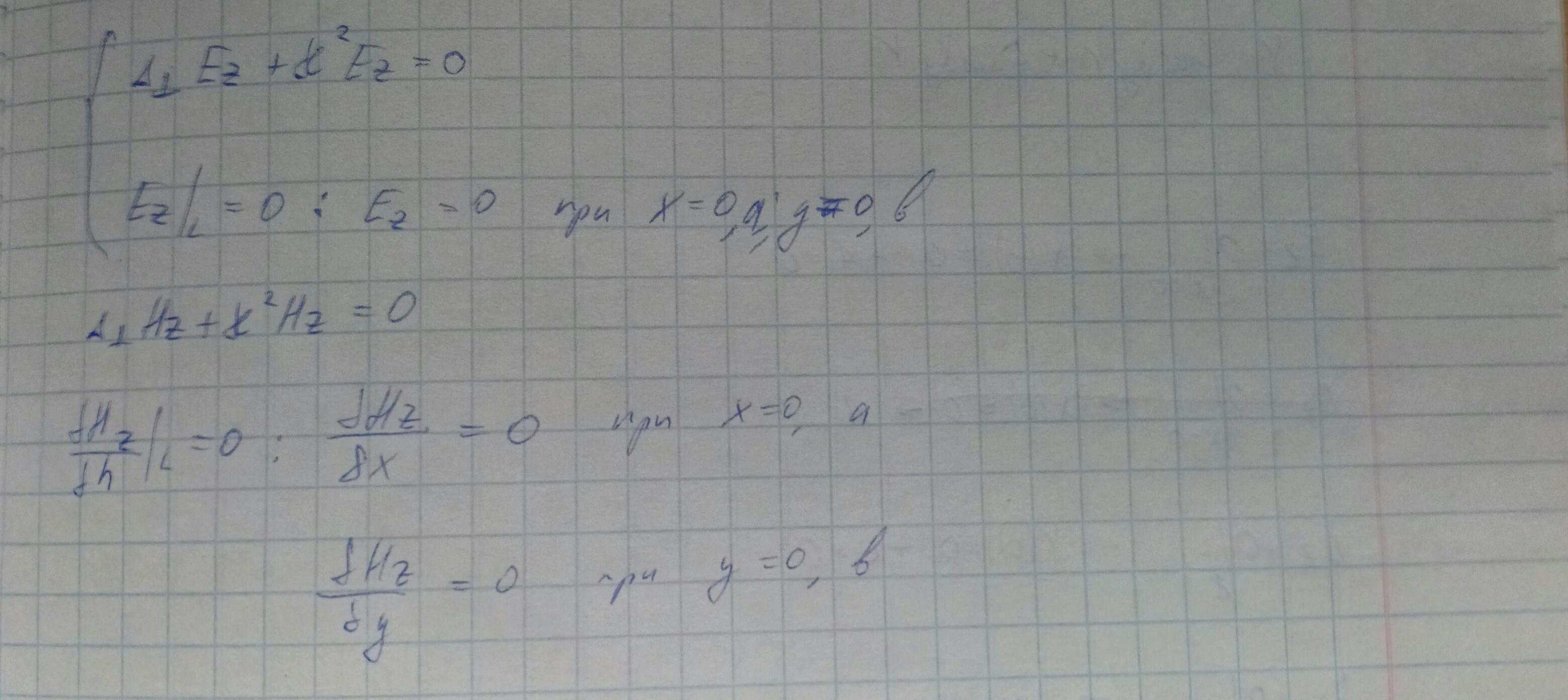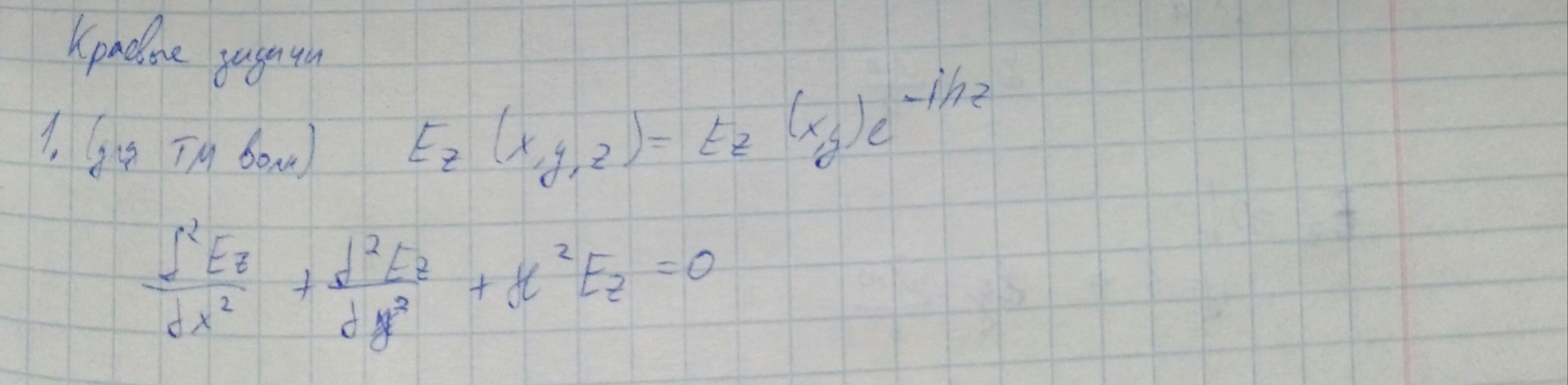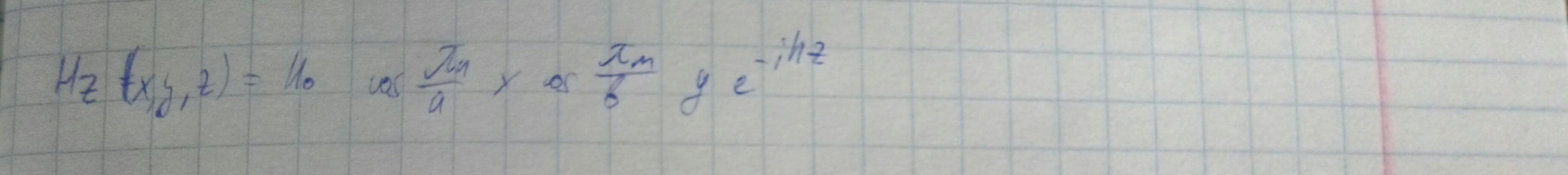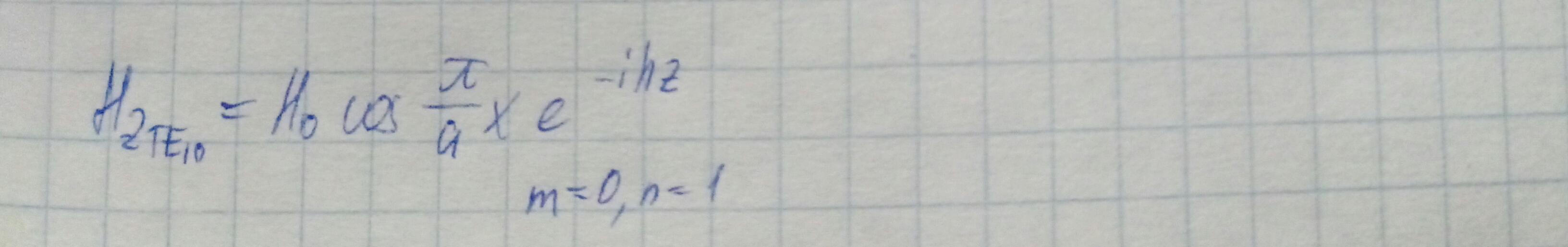| | Прямоугольный волновод, его параметры, понятие "низшей моды". |
Анализ распространяющихся в прямоугольном волноводе волн обычно опирается на решения уравнений Максвелла, получаемые с учётом граничных условий, которым должны удовлетворять поля на стенках волновода.
Прямоугольный волновод представляет собой полую металлическую трубку.
| | Прямоугольный волновод - регулярный волновод, имеющий в сечении прямоугольник. |
Выпишем выражение для длины волны в волноводе.

Запишем 2 краевые задачи. Итоговой целью является нахождение квадрата поперечного волнового числа.
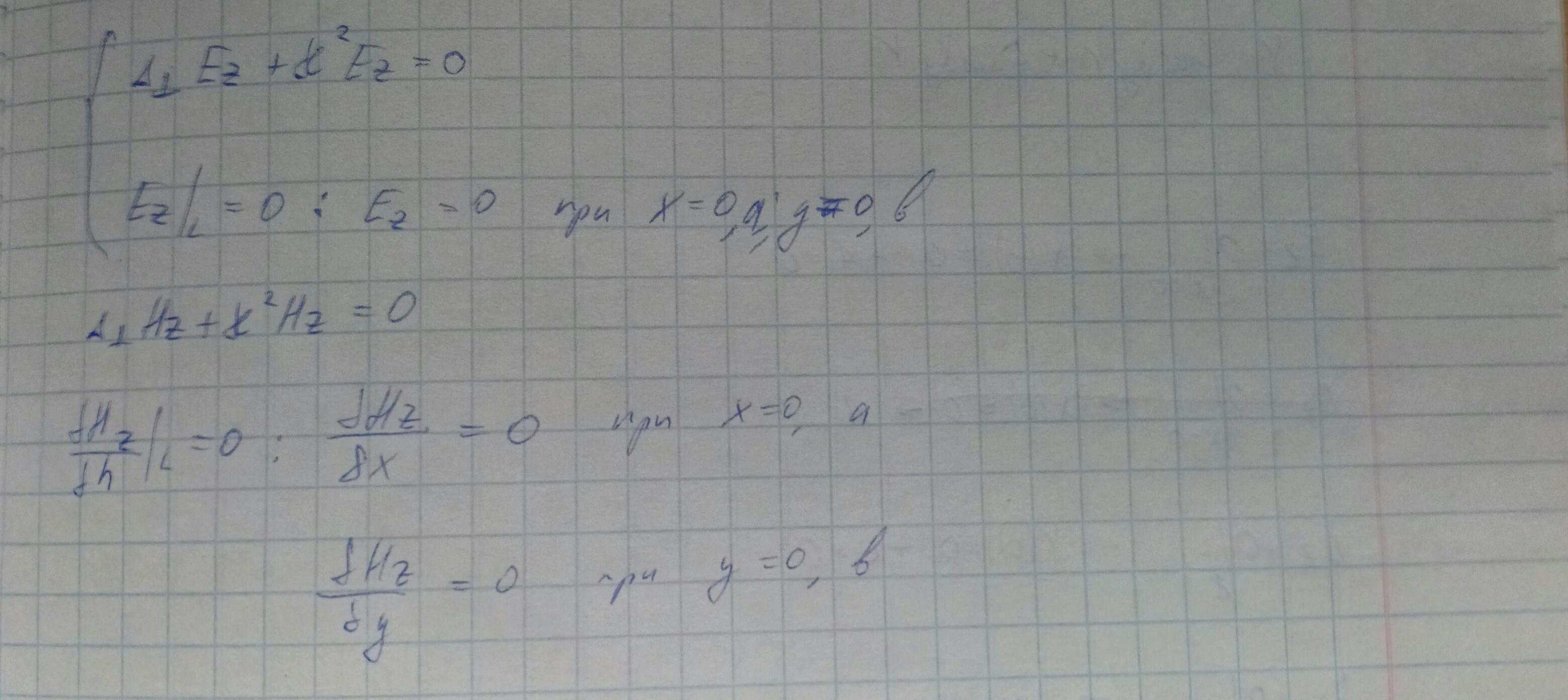
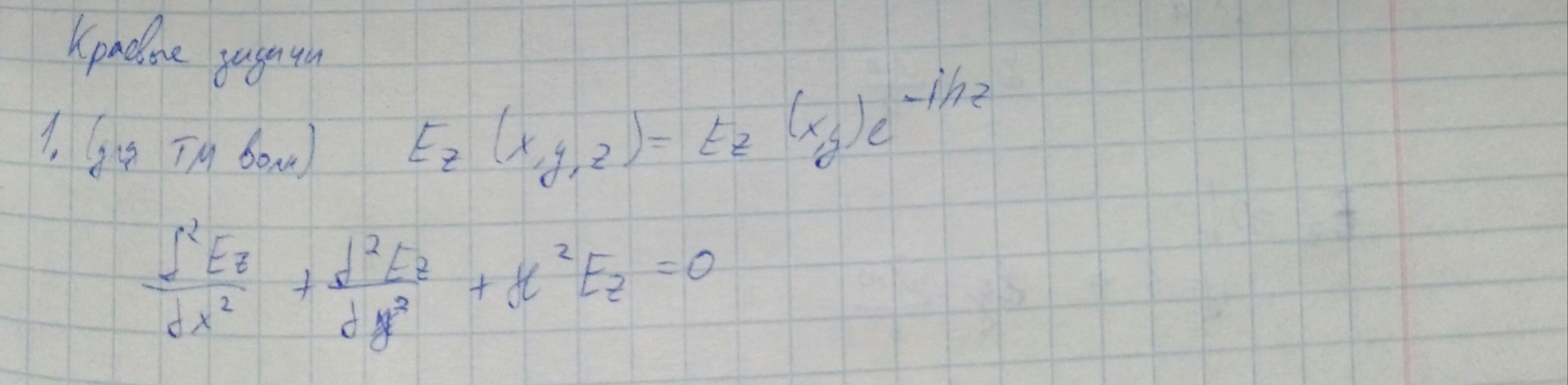
Решаем методом разделения переменных.
Ez= X(x)*Y(y), где x,y — независимые переменные
Поделим полученное уравнение на произведение X*Y

Поскольку первое и второе слагаемые зависят либо от x, либо от y и их сумма равна const, то по отдельности они тоже const.

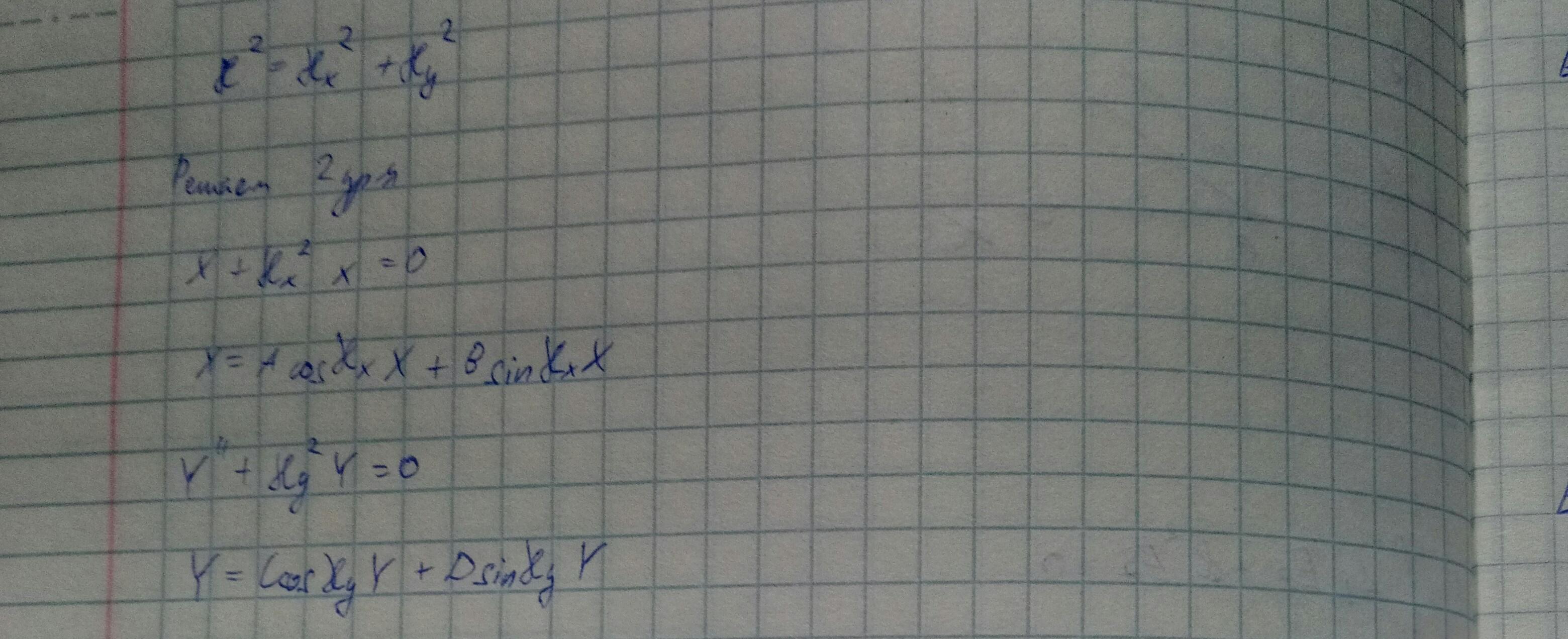
Рассмотрим границу x=0. На этой границе при любом y Ez должно обращаться в 0. Это означает, что на этой границе X должно обращаться в 0. Аналогично для нулевого значения Y.


Рассмотрим граничные условия Ez при x=a.
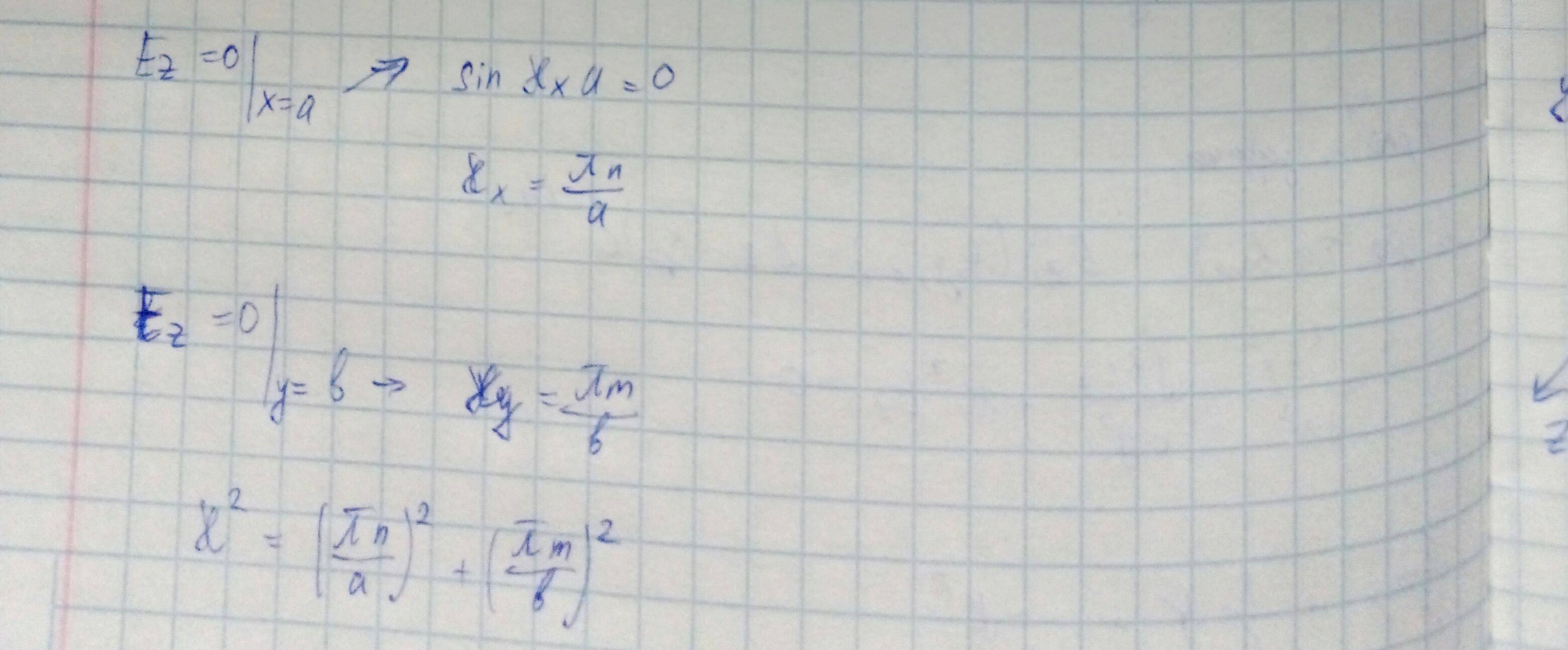
Наименьшее значение каппа соответствует волне H10 (индексы указывают значения n, m) и равно pi/ a. (Л.Д.Ландау, Е.М.Лифшиц "Электродинамика сплошных сред", стр. 440)
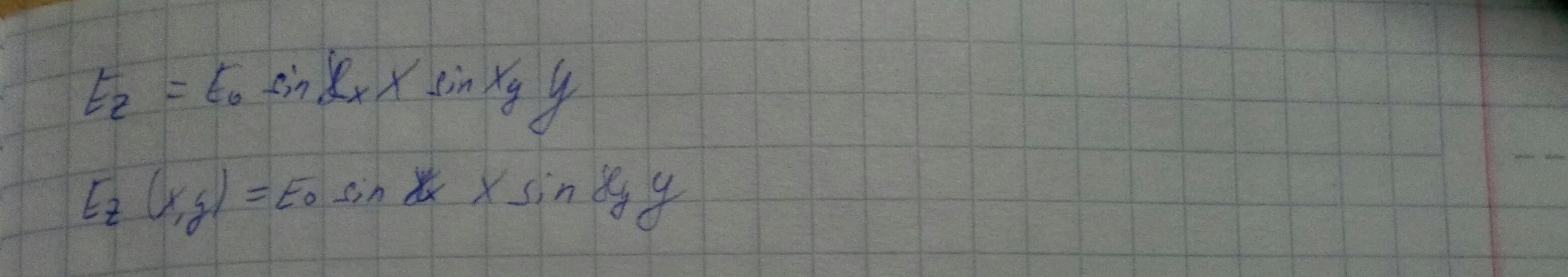

Чтобы перейти к реальным физическим полям, нужно перейти к мгновенным значениям. Суть этой операции заключается в умножении на e^(iωt) и взятии реальной части.
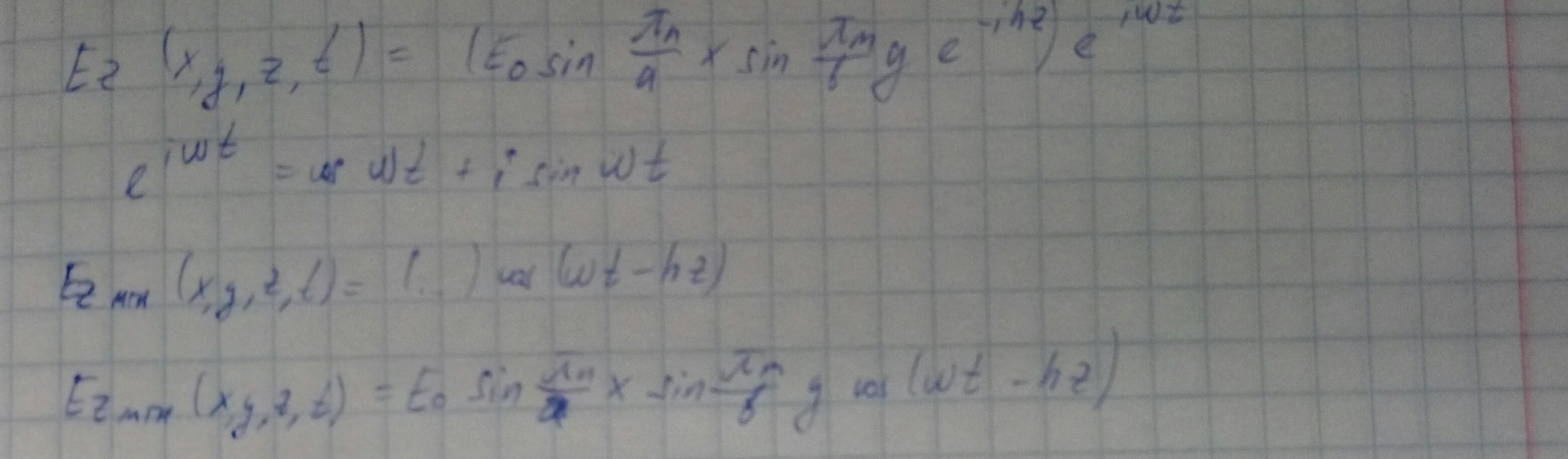
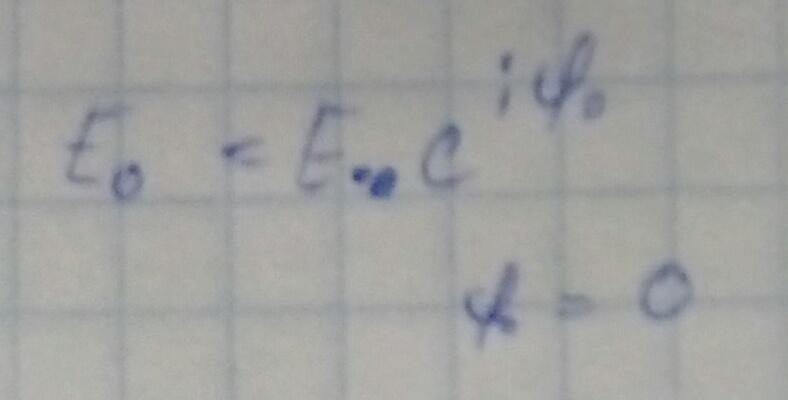 Для TM-волн ни n, ни m не могут обращаться в 0. n.m=1,2,3,...
Для TM-волн ни n, ни m не могут обращаться в 0. n.m=1,2,3,...
TMnm — конкретная мода
TE
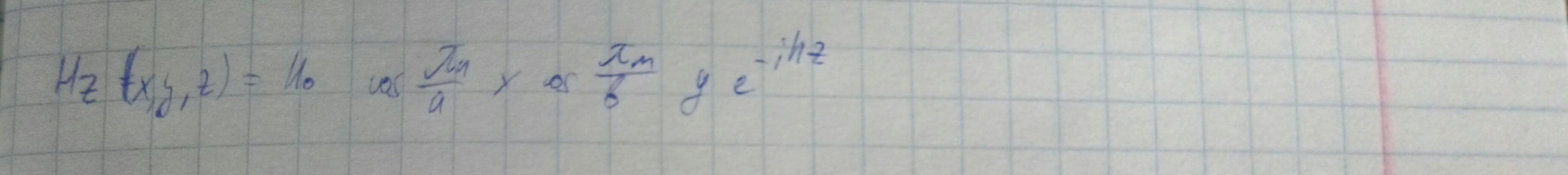
Либо n, либо m может обращаться в 0 (одновременно n и m не равны 0).
TEnm — конкретная мода
Первой распространяющейся модой является волна типа TE10 для рисунка ниже. Такая мода называется низшей.

Низшая мода используется в волноводной технике.
Если используем волновод между первой и второй критической частотой, то в волноводе может распространяться одна мода и в этом режиме всегда имеем предсказуемую структуру поля.
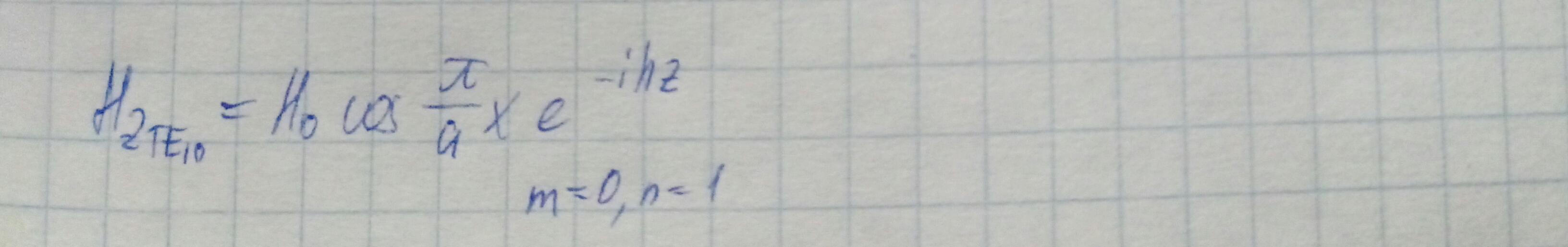


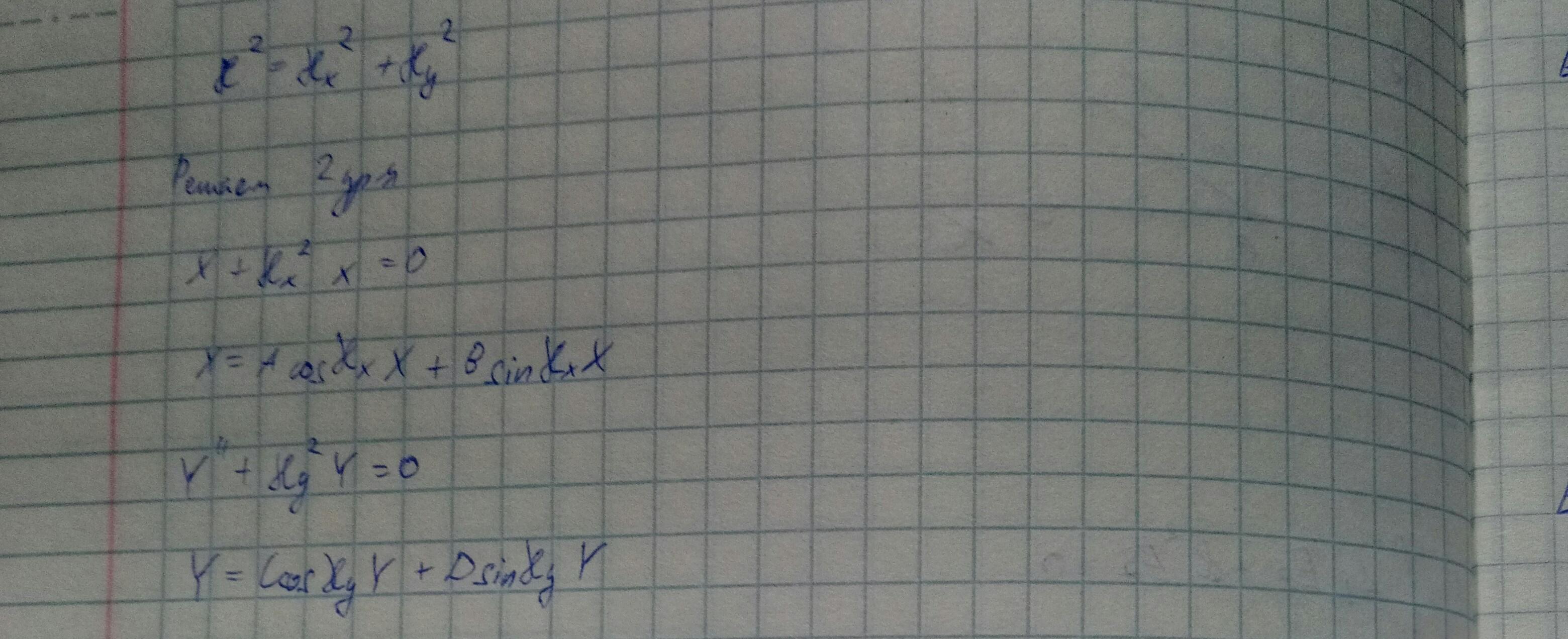


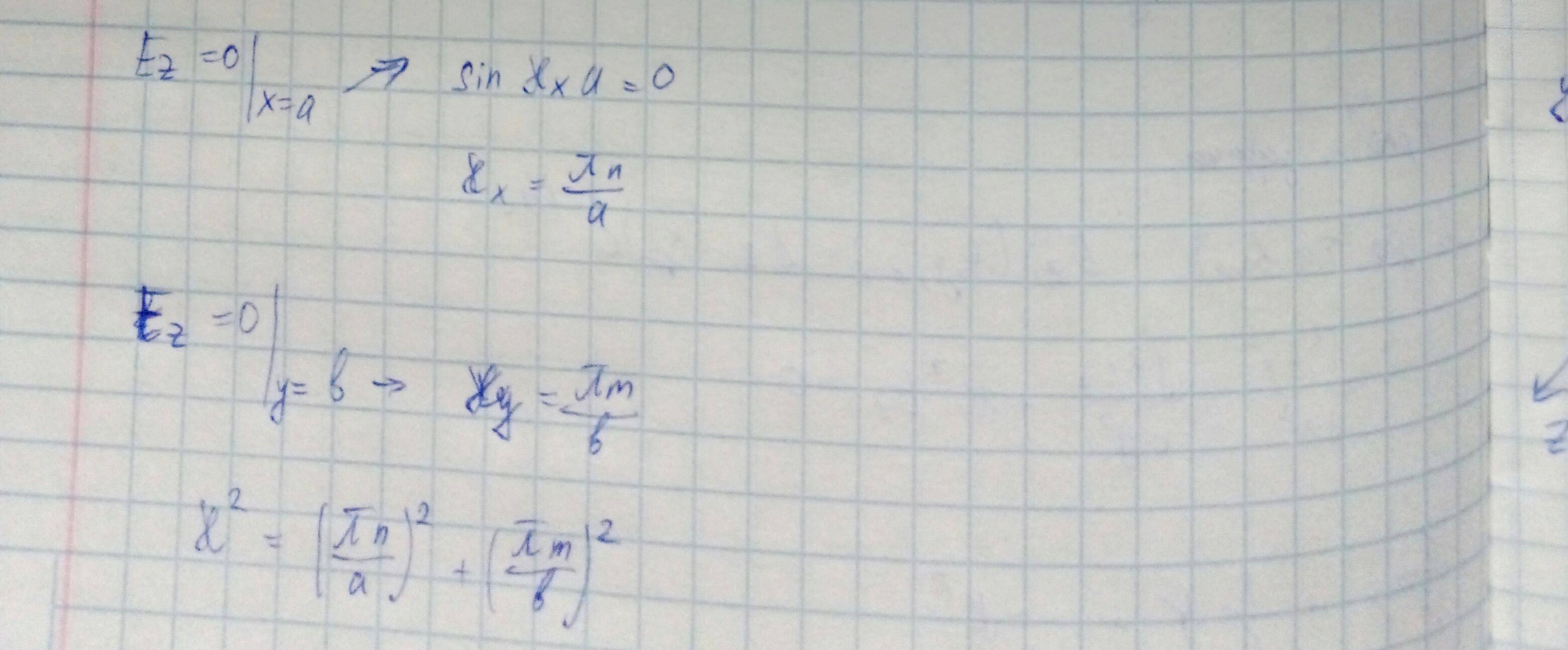
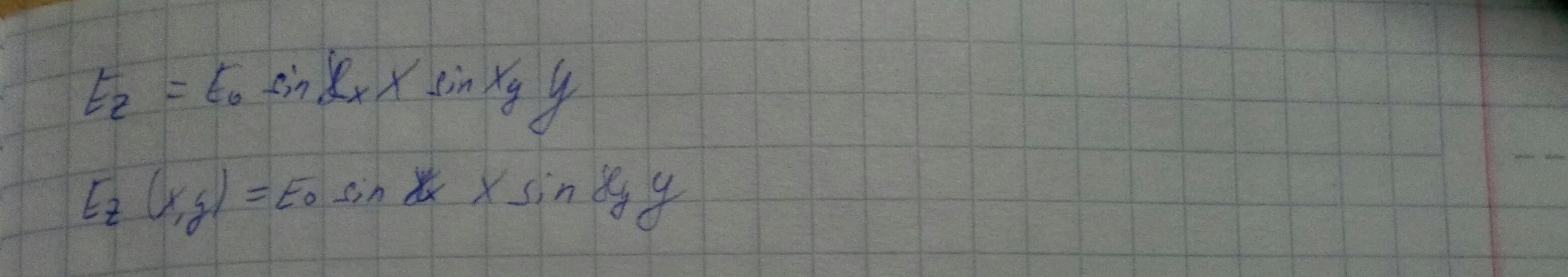

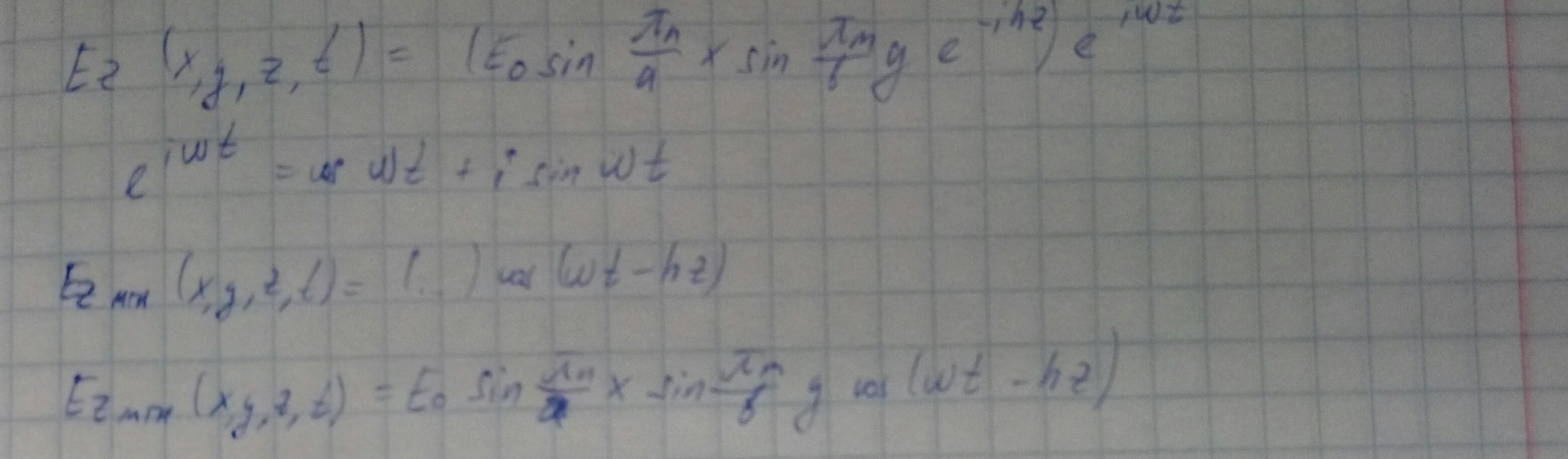
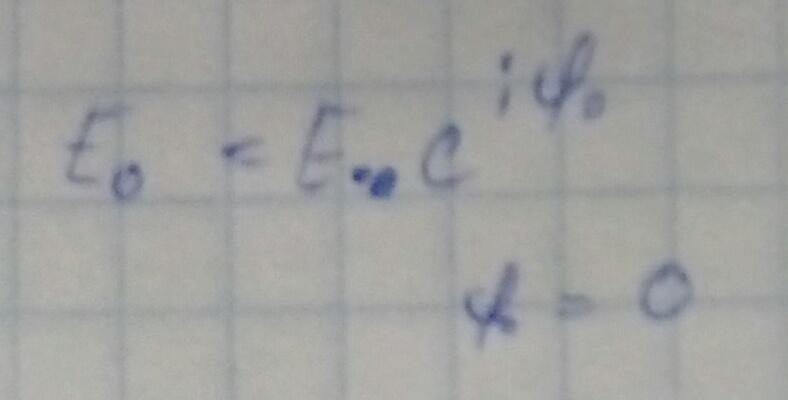 Для TM-волн ни n, ни m не могут обращаться в 0. n.m=1,2,3,...
Для TM-волн ни n, ни m не могут обращаться в 0. n.m=1,2,3,...