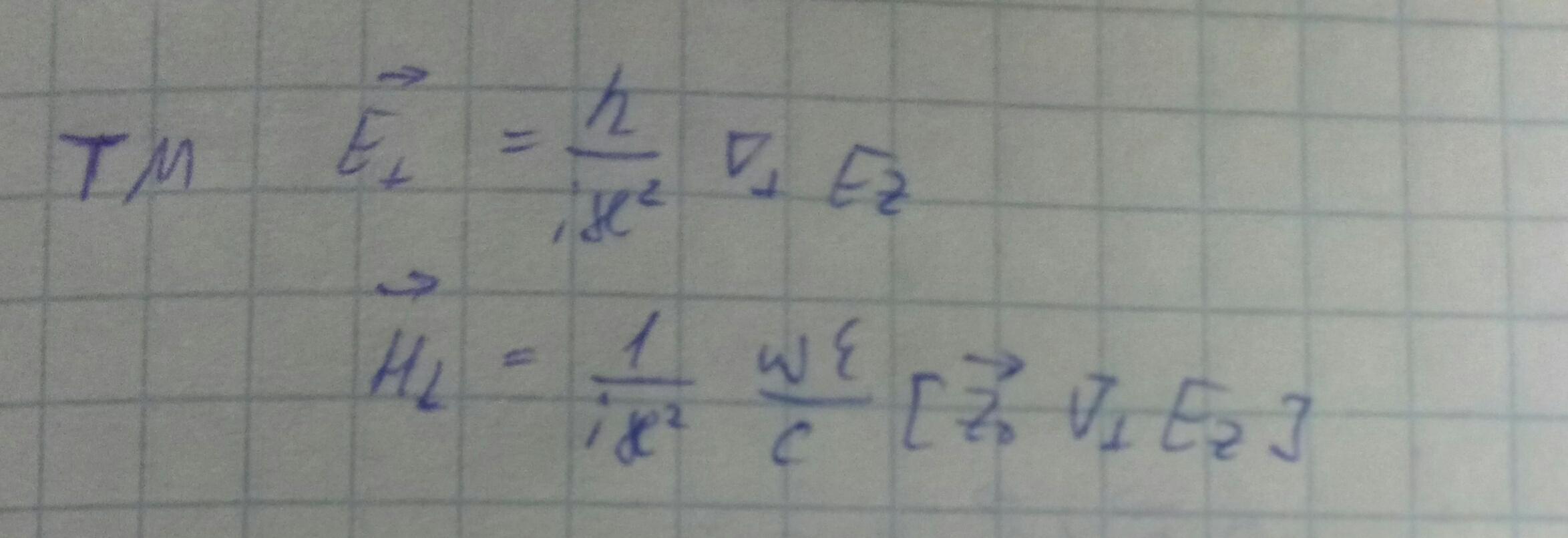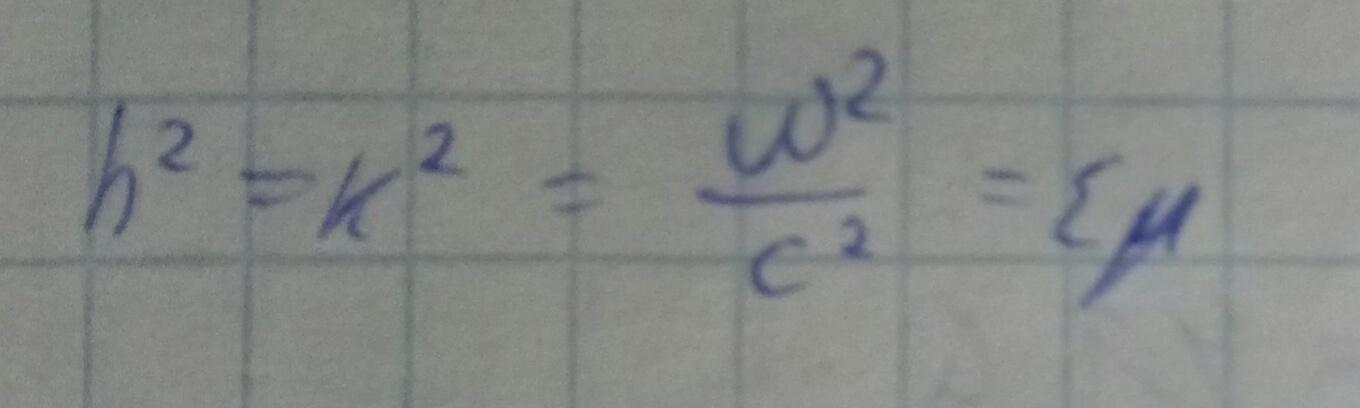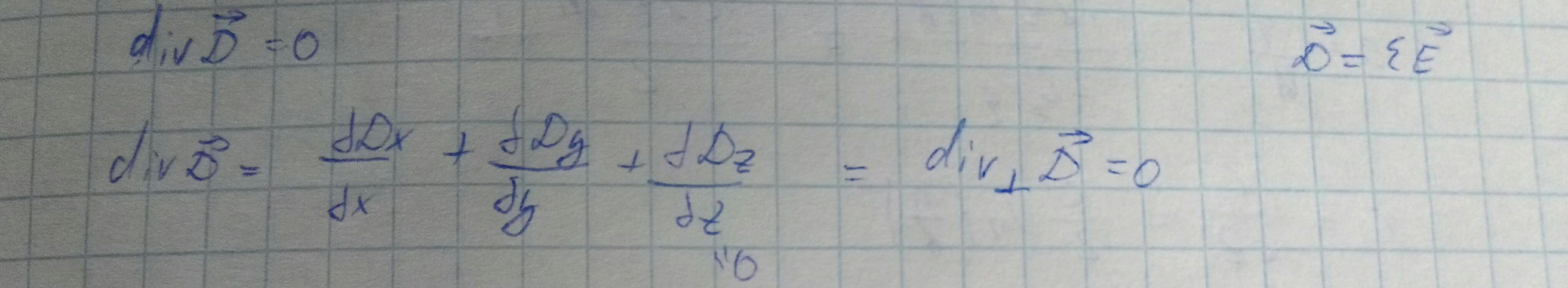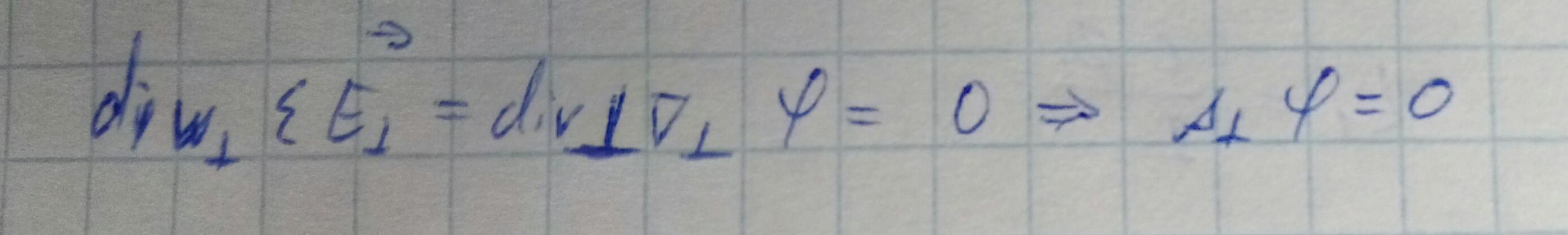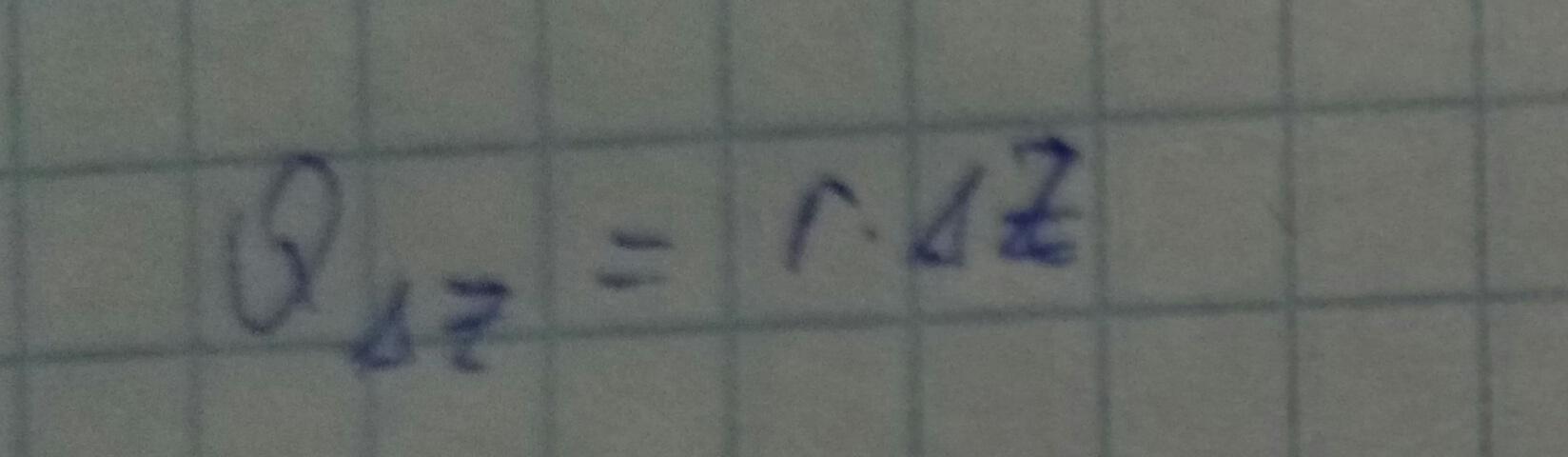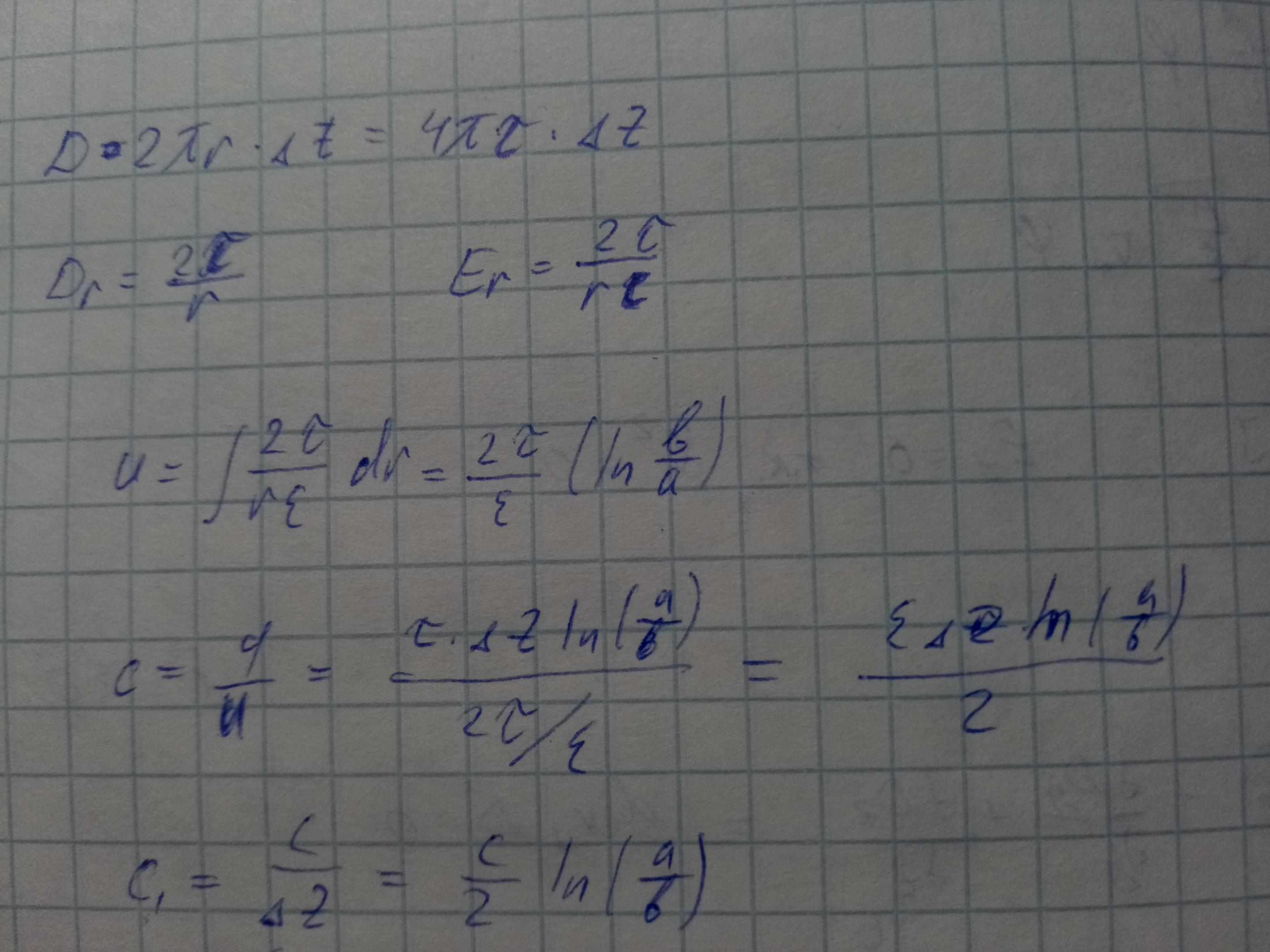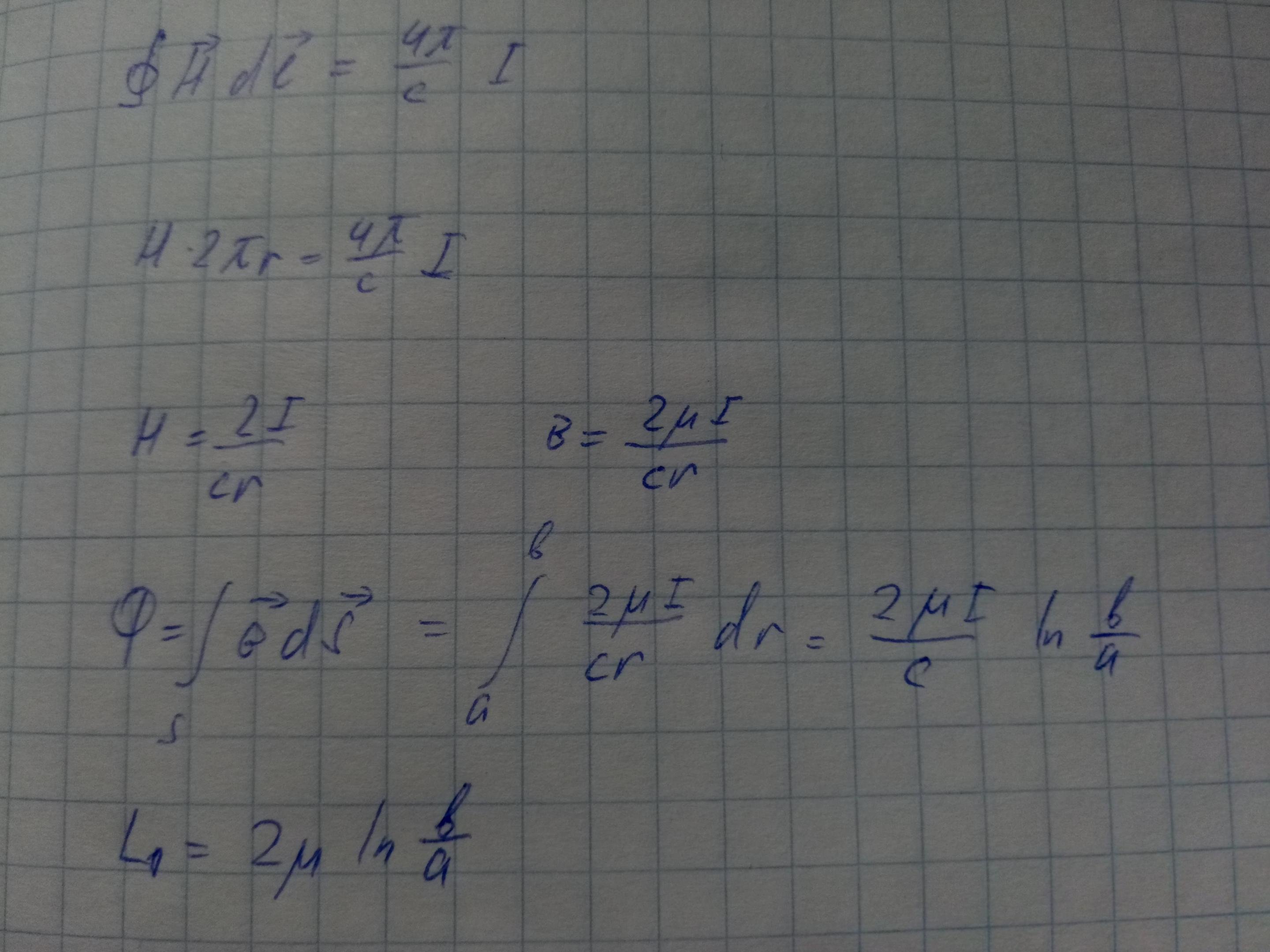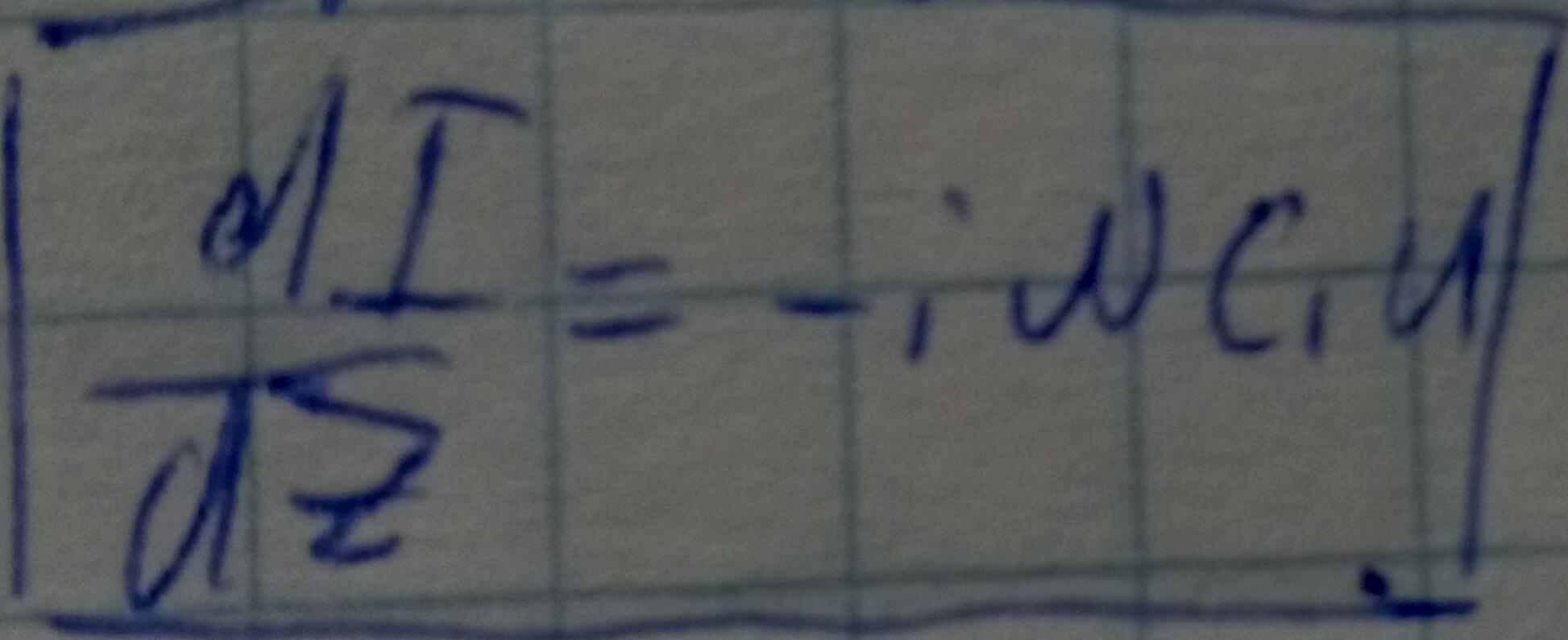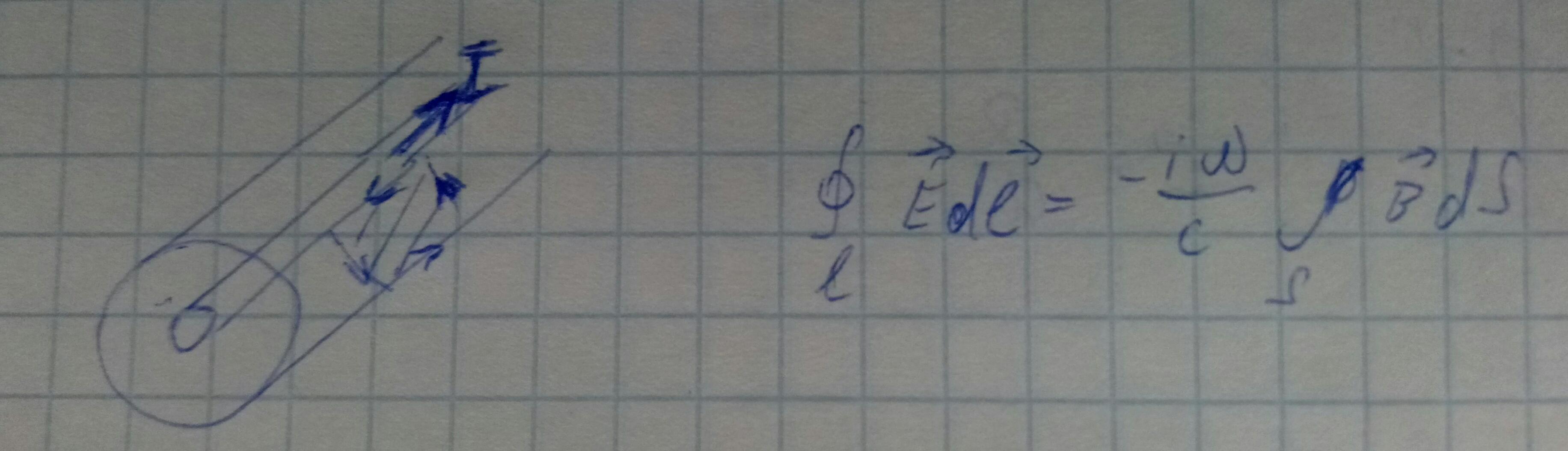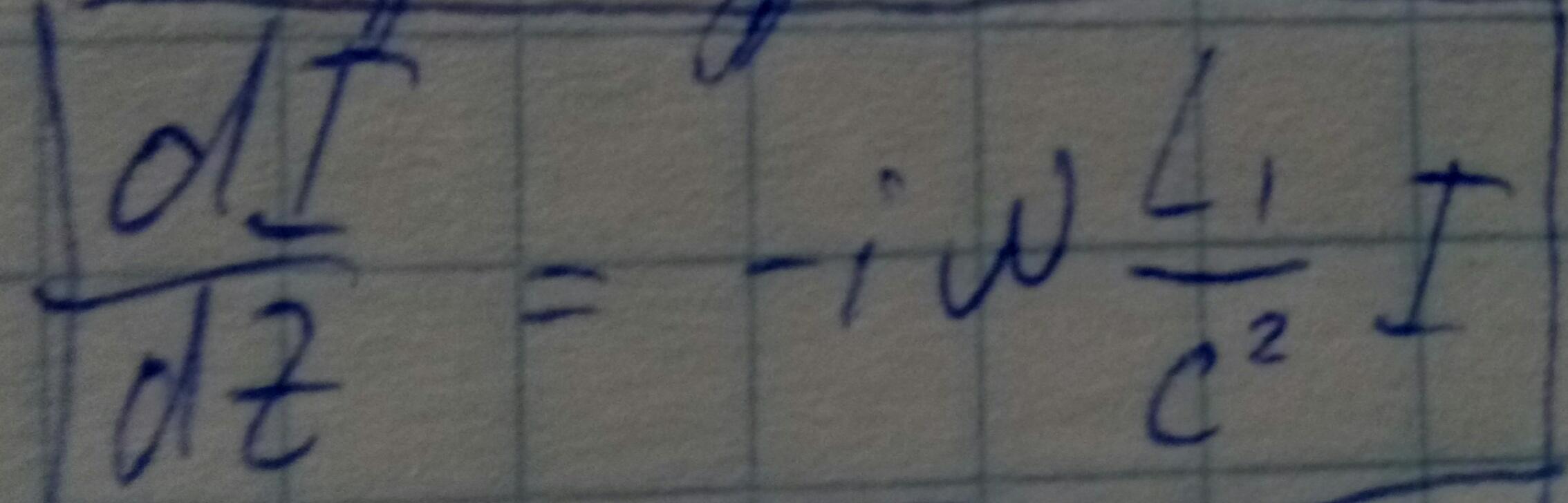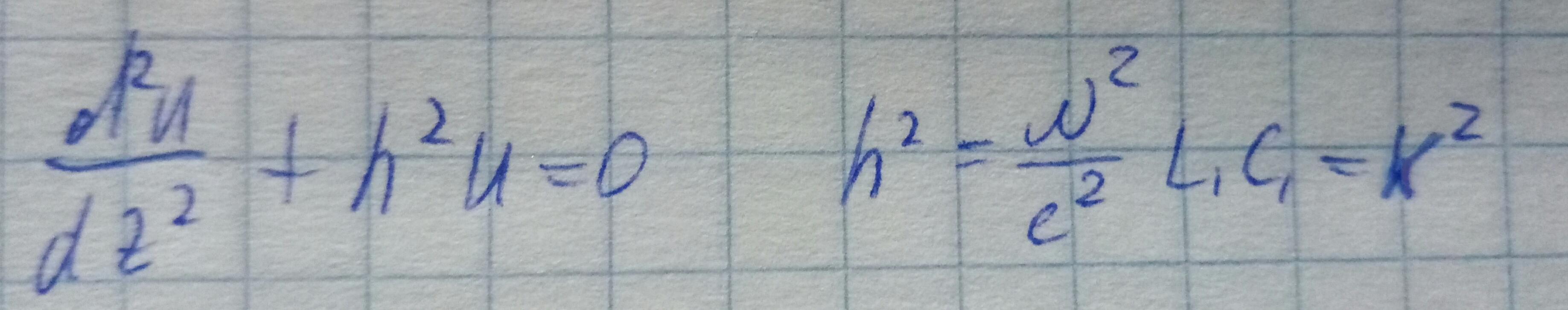| | TEM-волны, телеграфные уравнения. |
TEM-волны — плоская однородная волна в свободном пространстве. Такие волны характеризуются тем, что у них Ez=0 и Hz=0. Они распространяются только в тех структурах, где возможны статические поля. (Подробнее на сайте.)
Напишем формулы поперечных компонент через продольные.
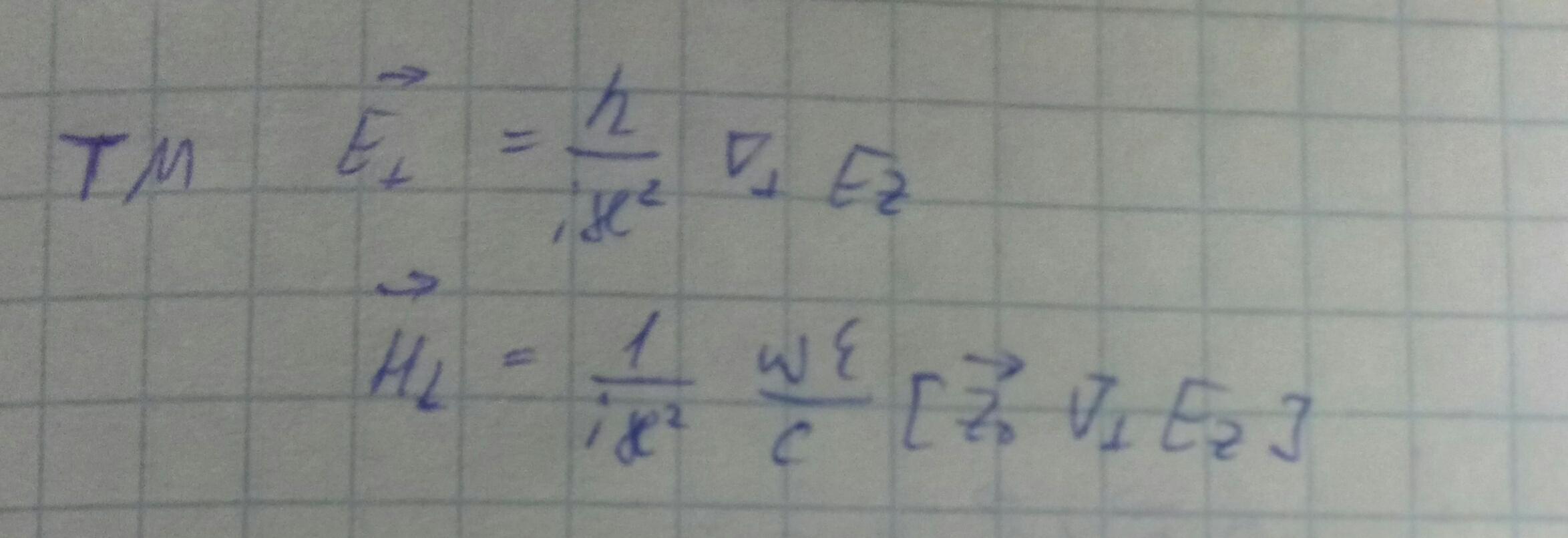
Есть шанс, что мы получим не равные 0 поперечные компоненты, если каппа^2=0(неопределённость 0 делить на 0).
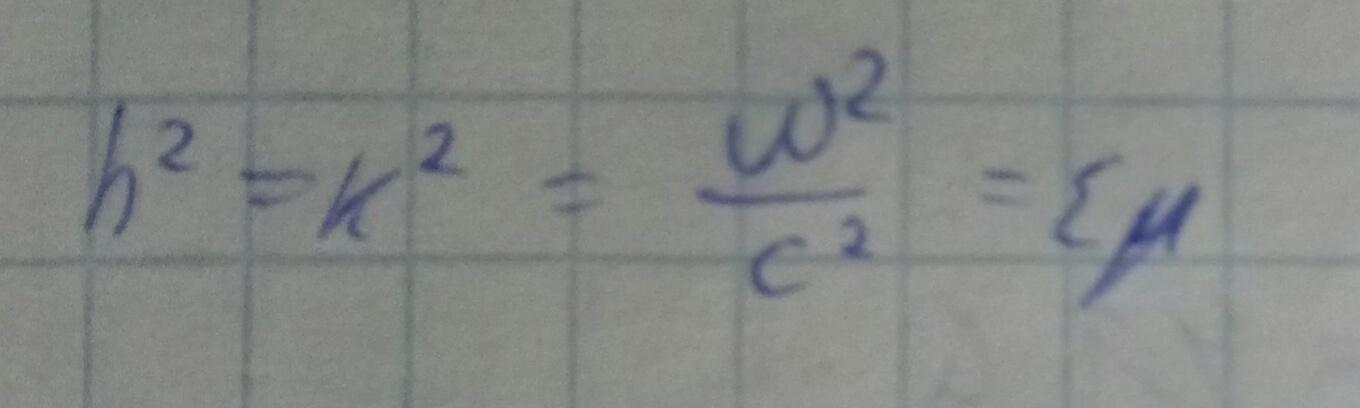
Выясним, что если такие волны существуют, то это будут волны без дисперсии, т.е. фазовая и групповая скорости похожи на фазовую и групповую скорости в свободном пространстве.
Волны без дисперсии позволяют передавать сложные сигналы на дальние расстояния без потерь.

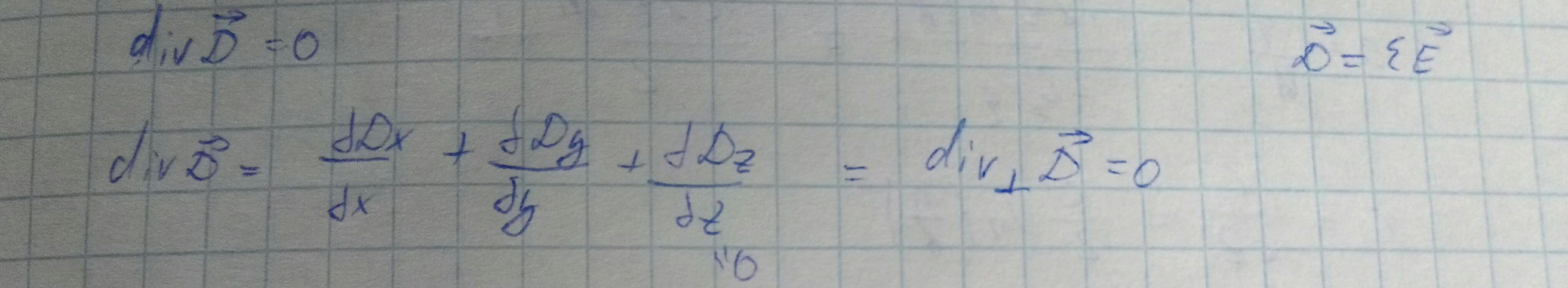
Если ε не зависит от координат, то получим следующее:
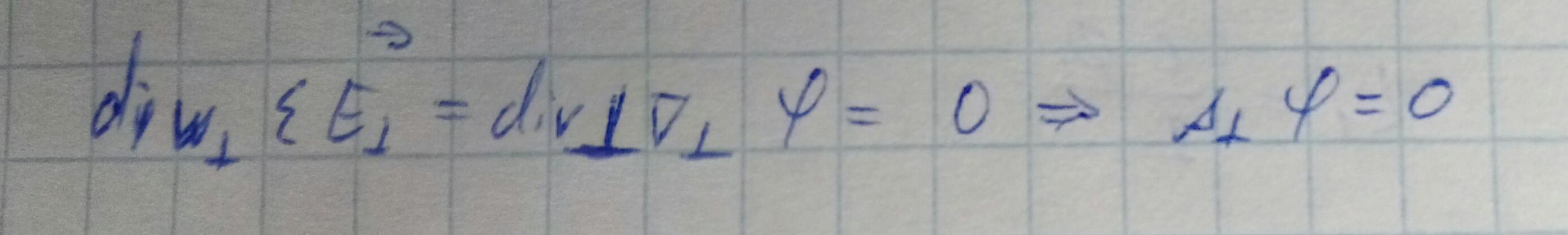
Следствия:
- TEM-волны возможны только в тех линиях передач, в которых могут существовать статические поля. От продольной координаты поле не зависит.
- Структура поля будет такая же, как в статике.
Какие волноводы могут поддерживать TEM-волны? Только многосвязные волноводы.
Например, коаксиальные волноводы. В них могут быть как статические, так и TEM-волны.
Односвязные волноводы (прямоугольные, круглые) не могут поддерживать TEM-волны.
Примеры многосвязных волноводов:
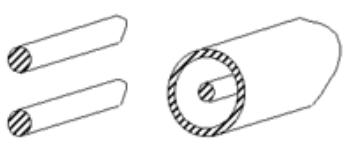
Вспомогательные задачи.
Рассмотрим коаксиальный волновод и найдём для него погонную C и погонную L.

Разместим на центральном проводнике заряд с линейной плотностью +τ, а на внешнем проводнике — -τ.
Возьмём участок Δz.
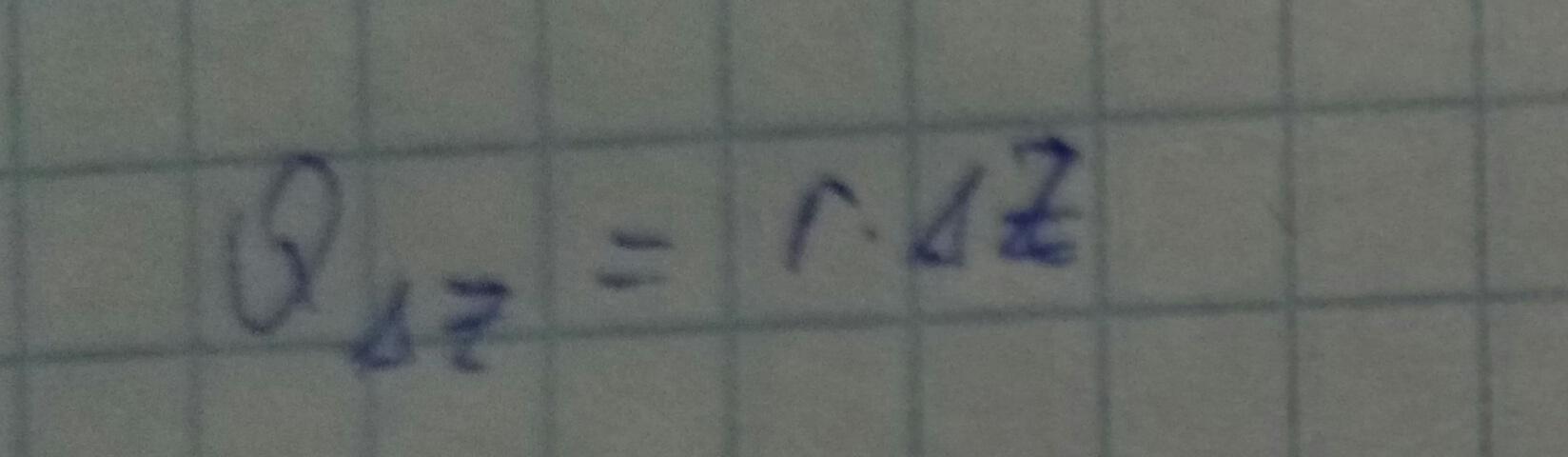
Нужно связать Q и U.
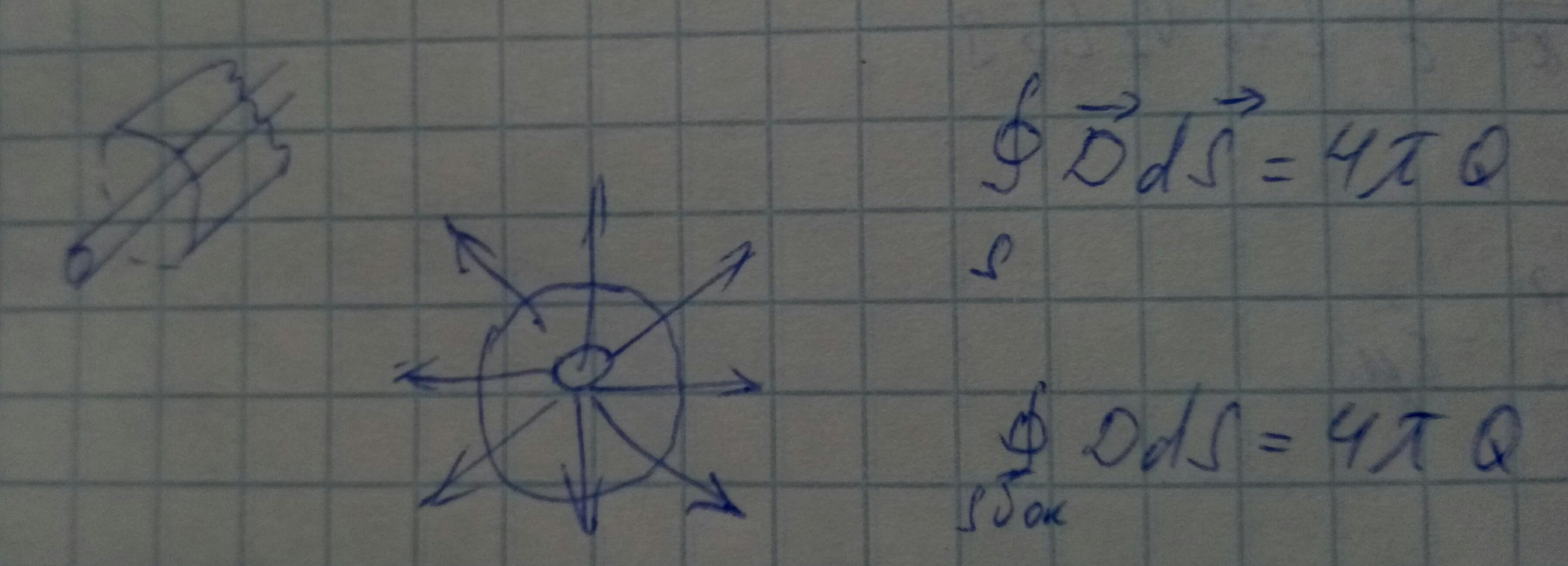
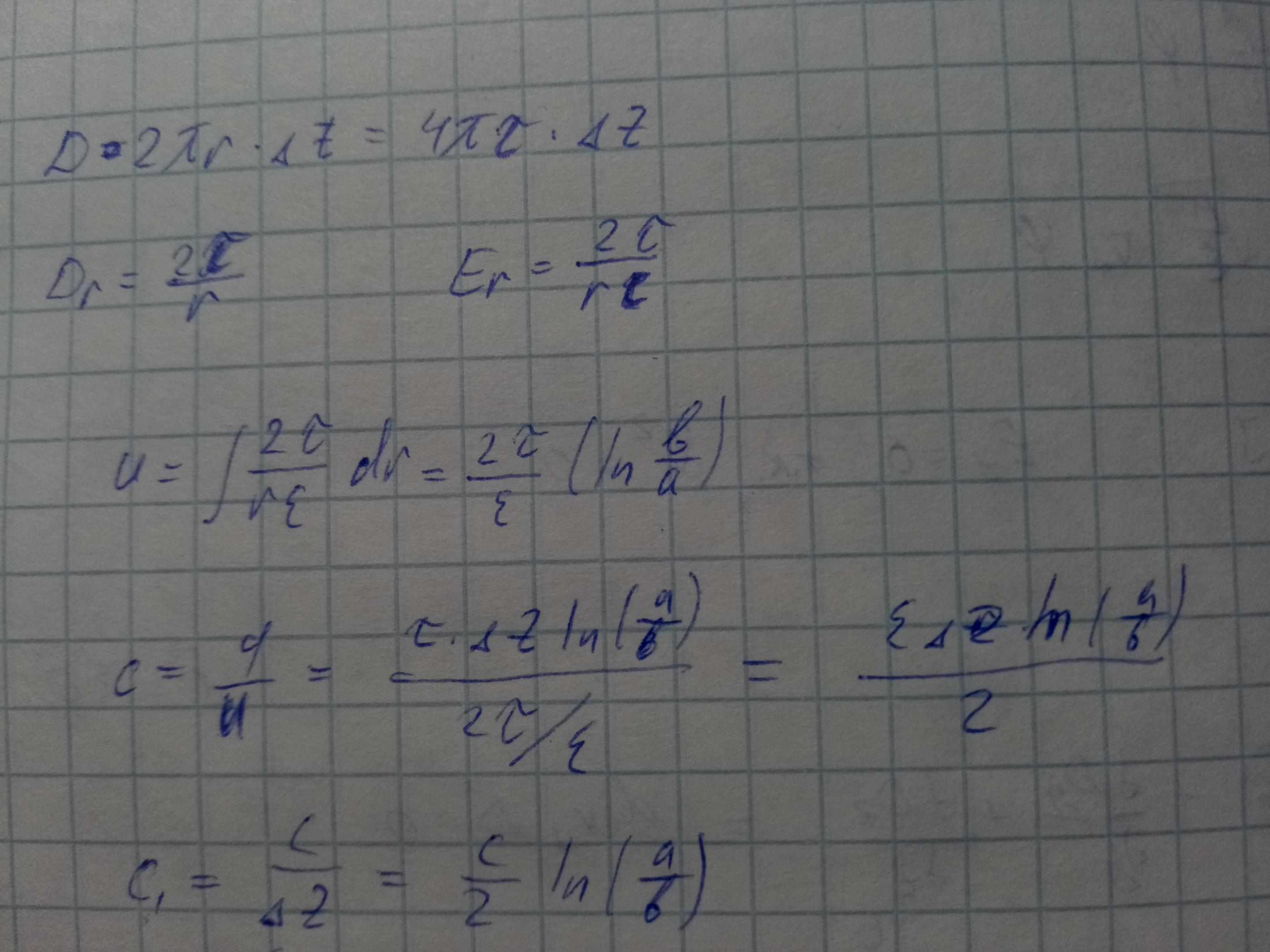
Рассмотрим коаксиальный волновод и найдём L1.
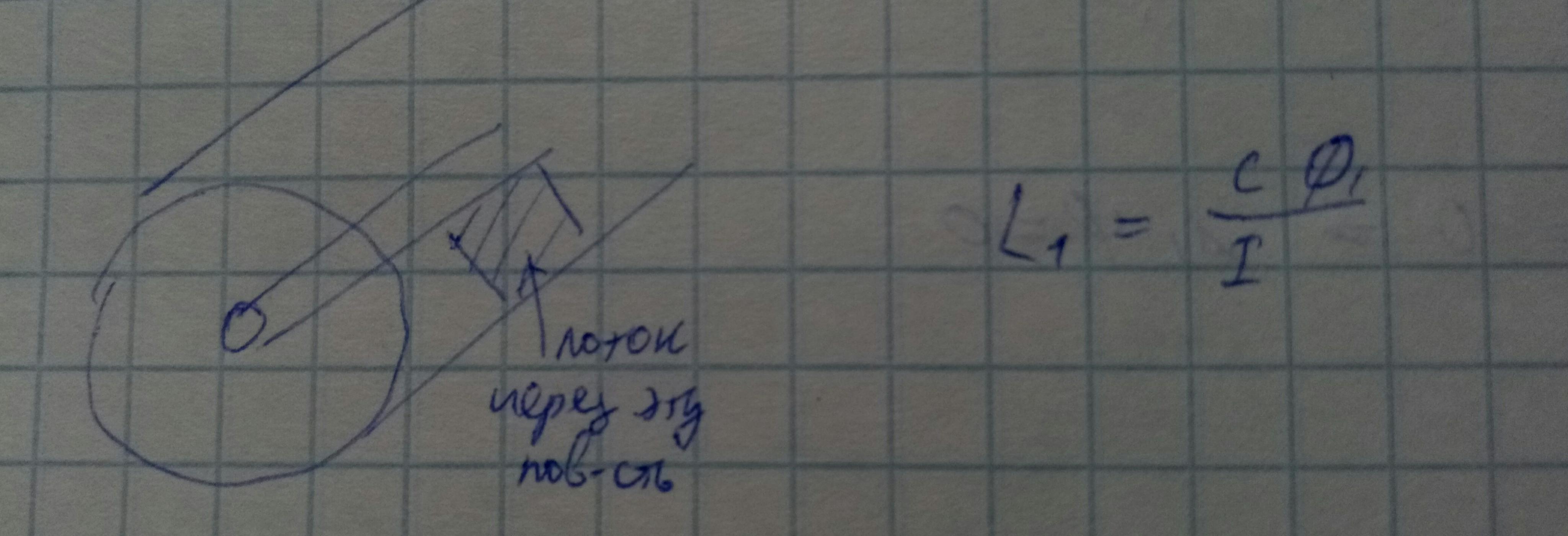
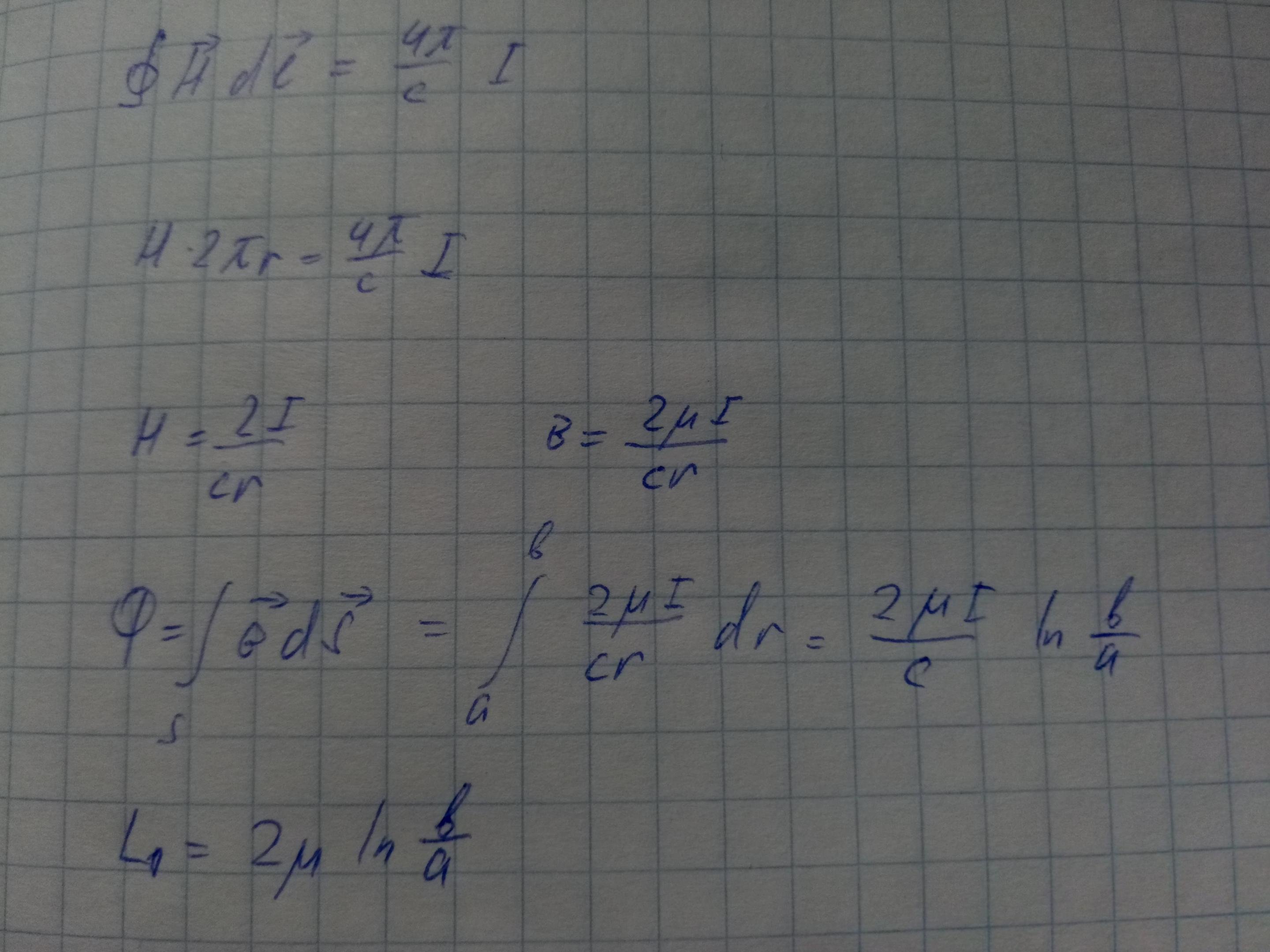
Телеграфные уравнения
Телеграфные уравнения важны с практической точки зрения, поскольку они упрощают процесс работы. Вместо полей вводят 2 скалярные величины (имеют зависимость от я) — I и U, они вводятся для конкретного сечения.Будем считать, что погонные параметры будут совпадать в статике и для TEM-волн.
Получим первое уравнение.

Первое уравнение:
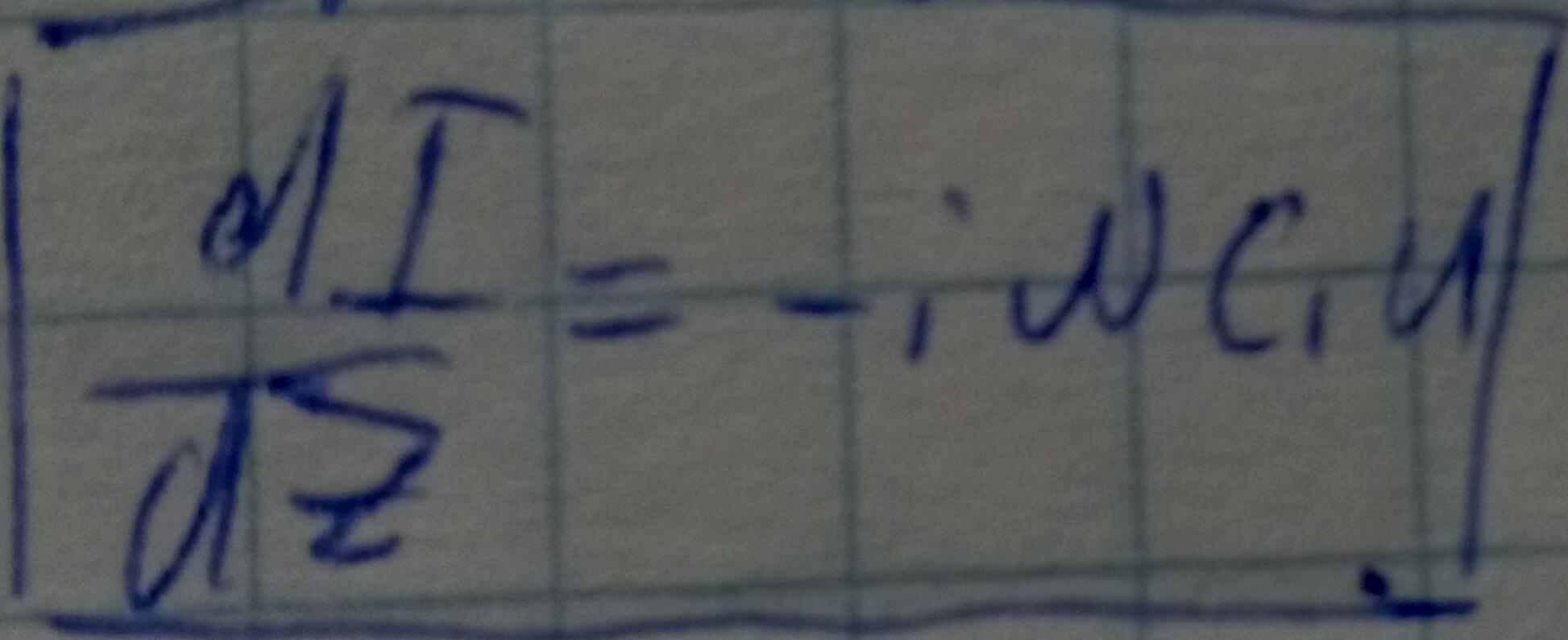
Аналогично получим второе уравнение.
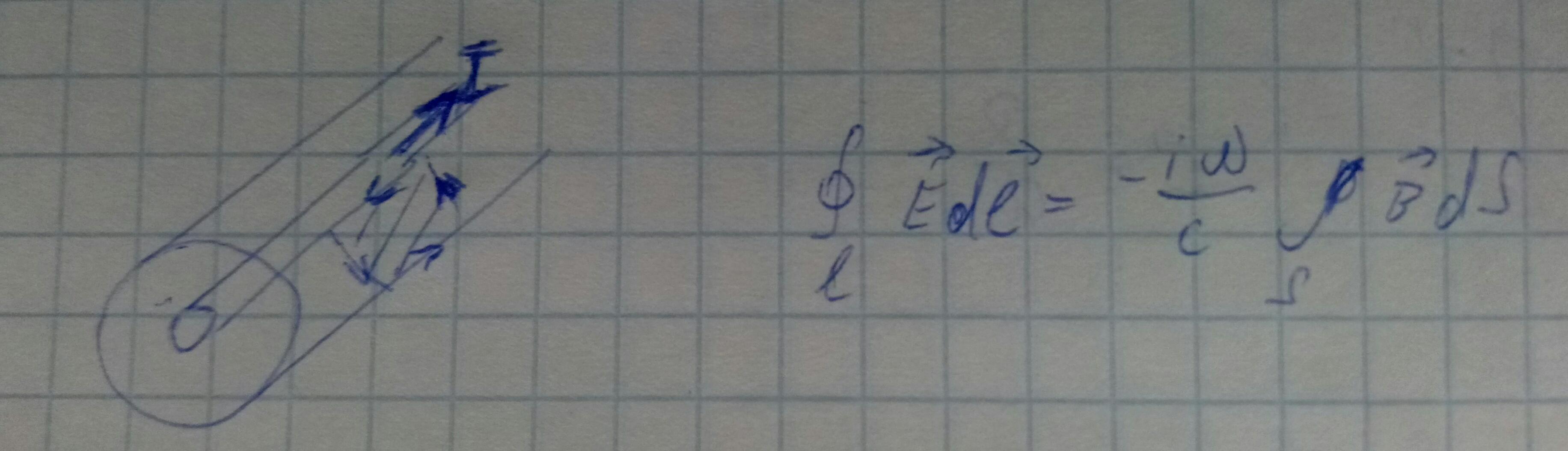
Второе уравнение:
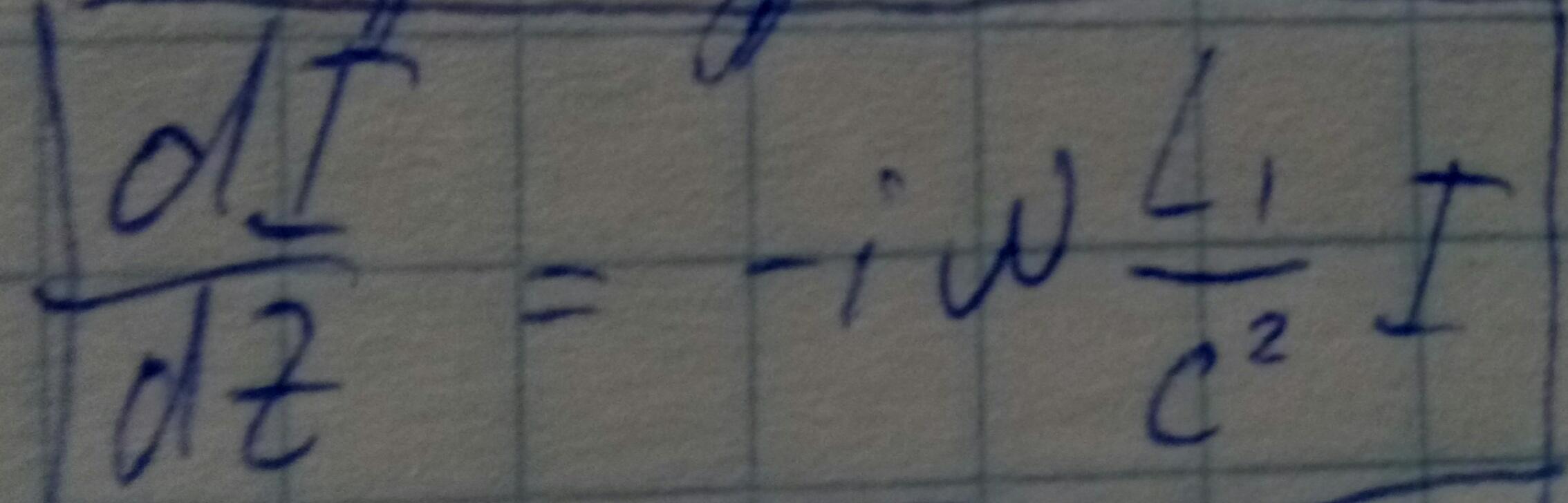
Оглавление