Описание метода:

Математика дает изобретателю ресурсы для решения задач, если изменяемый объект при некоторых допущениях (упрощениях, не влияющих на выполнение объектом функции) превращается в математическую абстракцию, которая имеет четко определенные математические свойства. Перенос этих математических свойств с абстракции на объект и позволяет решить задачу с большим эффектом и с меньшими затратами. Или, по-другому, для решения объект изменяется так, чтобы быть максимально похожим на математическую абстракцию.

Математическим эффектом называется применение свойств математических абстракций для разрешения противоречий или облегчения выполнения каких-то действий.

Например, чтобы трамбовать квадратные поверхности с помощью вращающегося катка, используют каток в виде конуса со скошенным основанием.

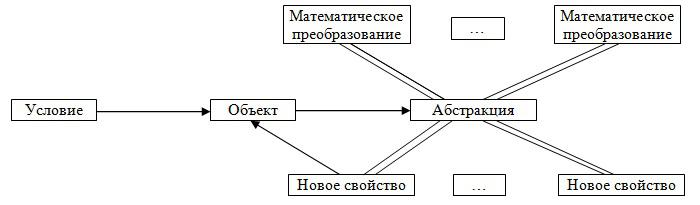
Математический эффект содержит 4 элемента:

- объект, который надо изменять;

- условие, превращающее объект в ту или иную абстракцию;

- математическое преобразование над этой абстракцией (набор преобразований);

- свойство, которое дает преобразование абстракции или свойство самой абстракции, передаваемые объекту.

Схематически изобразим это так:

История развития цивилизации показывает, что любая строго доказанная математическая абстракция рано или поздно находит свое реальное воплощение. Т.е. математика не абстрактна, а реальна, просто наши знания об окружающем мире примитивны, на уровне арифметики.

Наиболее хорошо математические эффекты показаны на примере геометрии.

В отличие от ХЭ, позволяющих преобразовывать вещества с поглощением или выделением энергии, или ФЭ, позволяющих преобразовывать энергию, ГЭ обычно перераспределяют имеющиеся потоки вещества и энергии.

Примеры геометрических эффектов.

Для уменьшения наружного диаметра электрического кабеля при той же эффективности передачи энергии предложено изготовлять его из жил, имеющих не круглое, а трапециевидное сечение. При этом резко уменьшаются промежутки между жилами, занимавшие в обычном кабеле до четверти всего объема.

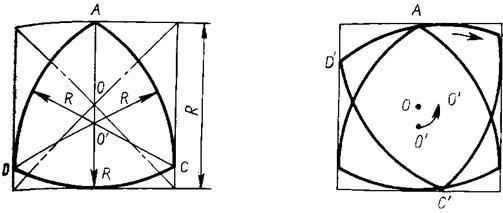
Использование сверл и фрез в виде треугольника Рело позволяет сверлить квадратные отверстия (см. рис.)

Применение ленты Мёбиуса особенно эффективно везде, где используются замкнутые ленты — в фильтрах, носителях информации и т. д. Благодаря тому, что классическая лента Мёбиуса является односторонней поверхностью, удается вдвое повысить срок службы шлифовальных лент на ее основе по сравнению с обычными кольцевыми.

Применение ГЭ для решения изобретательских задач можно найти в книге И. Л. Викентьев, В. И. Ефремов «Кривая, которая всегда вывезет. Геометрия для изобретателей» (сборник «Правила игры без правил» / Сост. Селюцкий А. Б. – Петрозаводск: Карелия, 1989, 280 с. Ссылки http://bookfi.org/book/730052, http://eknigi.org/nauka_i_ucheba/83201-pravila-igry-bez-pravil.html )

В перечне типовых приемов устранения ТП Альтшуллера к математическим эффектам можно отнести следующие приемы:

Принцип асимметрии, принцип матрешки, принцип сфероидальности.

Инструкция

Выход на эффект при решении задачи

1. Сформулировать ИКР для состояния решения.

2. Составить список доступных ресурсов.

3. По каждому вещественно-полевому ресурсу найти в базе знаний особенности, допускающие те или иные математические абстракции.

4. Используя справочник по математике и указатель геометрических эффектов, по каждой особенности подобрать рекомендации и примеры использования.

5. По каждой рекомендации составить принцип (механизм) реализации ИКР.

6. Оценить полученные идеи и выбрать наиболее вероятные (наиболее просто реализуемые).