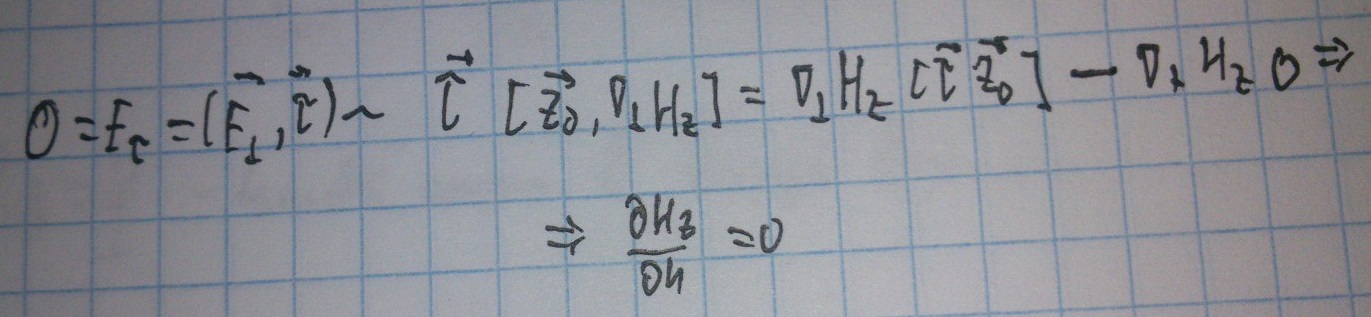(к оглавлению)

Введение: постановка задачи теории волноводов

 Пусть есть две точки: А и B

Перед нами стоит несколько задач, которые мы должны осуществить посредством электромагнитных волн: 
1) передать информацию от точки А к точке В
2) передать энергию от точки А к точке В

 Возможные способы решения:

1) Свободное пространство

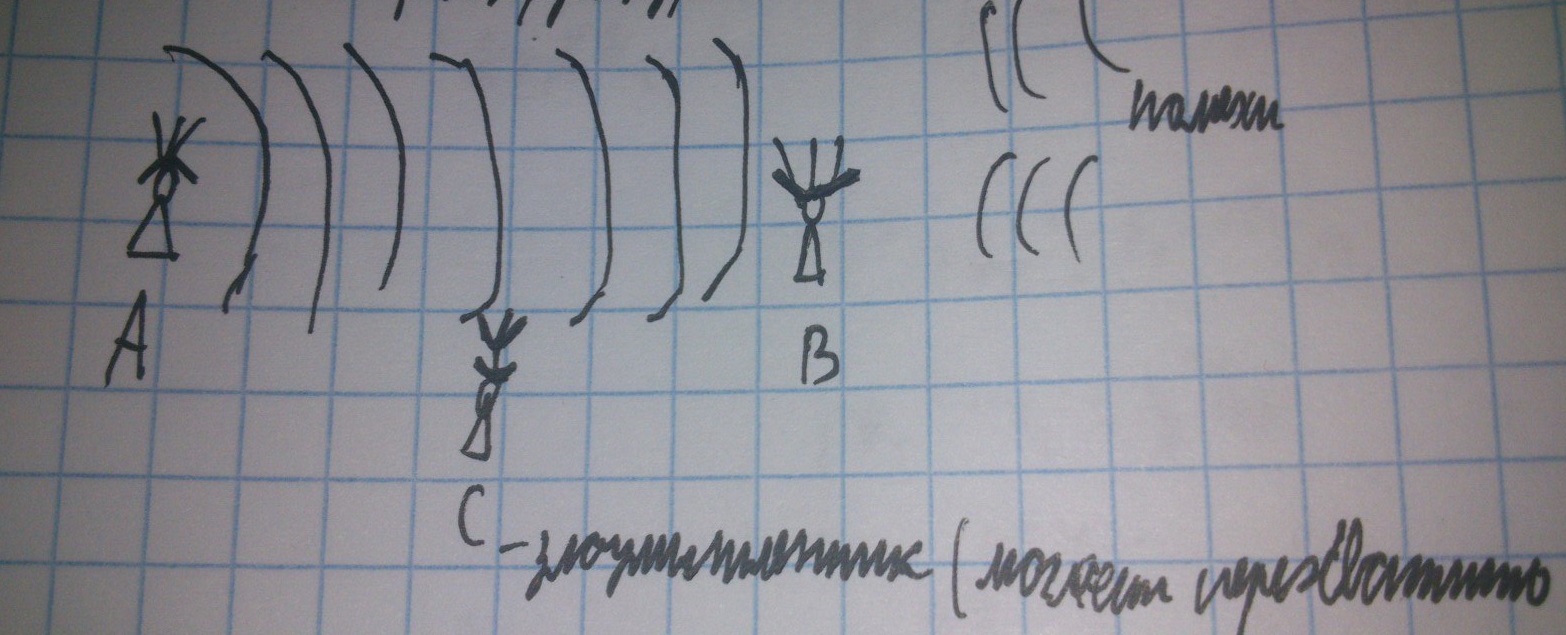
В таком случае заметно влияние помех. Помехи уменьшают скорость передачи, могу переводить приемник в нелинейный режим, уменьшать диапазон приемника и влияют на другие его характеристики. К тому же сигнал может перехватить злоумышленник. Также происходит рассеивание энергии, с которым борются с помощью конструкции антенн. Из других недостатков примечательно требование высокой мощности, и сложная реализация. Однако есть и плюсы, среди которых дешевизна производства и возможность сделать точки А и В мобильными.

2) Волноводная передача

В этом случае отсутствует рассеивания энергии. Также при волноводной передаче сложней прослушать передаваемый материал и влияние шума куда меньше. Среди недостатков можно выделить  дороговизну производства и отсутствие возможности сделать источник и приемник мобильными. 

Рассмотрим подробнее, что же такое волновод:

Классификация волноводов по их конструктивным особенностям:

1) По наличию внешнего экрана

• Закрытые (экранированные) - электромагнитное излучение не проникает за стенки волновода

• Открытые - выполнены аналогично закрытым, но снаружи не металл, а диэлектрик. Электромагнитное излучение не проникает за стенки волновода

2) По порядку связности

• Односвязные. Например, прямоугольный.
• Многосвязные. Например, коаксиальный.
• Нулевой связности. Такое возможно при отсутствии проводящих поверхностей

 3) По происхождению

• Естественный. Например, литосферный волновод (базальтовый слой)
• Искусственный

4) По зависимости поперечного сечения от продольной координаты

• Регулярный
• Нерегулярный
• Периодические

 Описание регулярного волновода

Для описания будем использовать комплексные амплитуды и  рассматривать только гармонические во времени поля. 

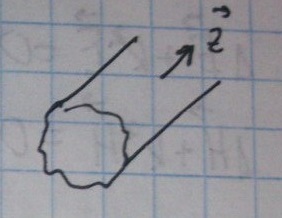
Рассмотрим регулярный волновод.

Запишем уравнения Максвелла без источников и подставим в них выражения для полей: 

Запишем роторы напряженности электрического и магнитного поля (в декартовой системе координат):

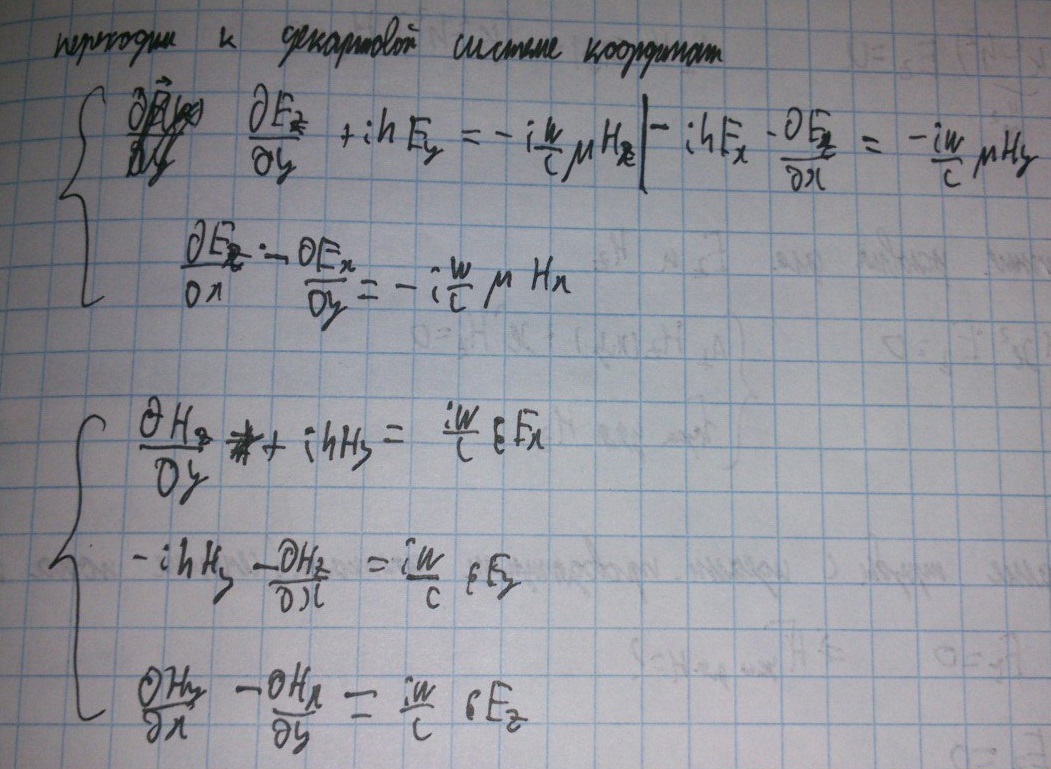
Преобразуем системы, чтобы выразить поперечные компоненты полей через продольные:

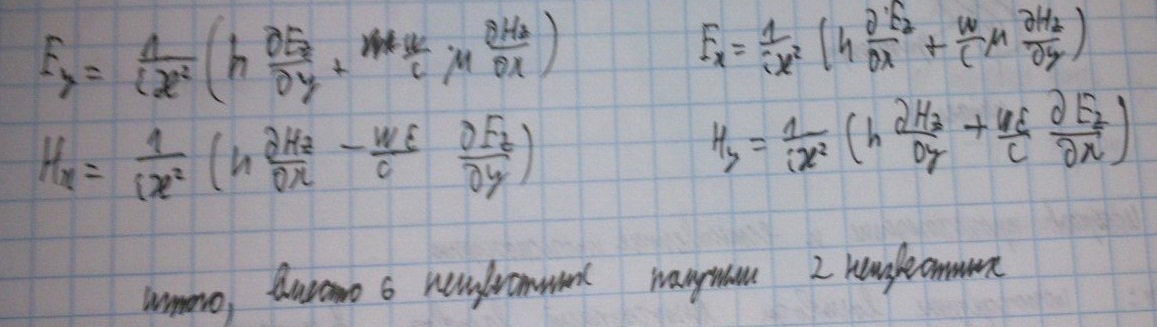
Или же в векторном виде:

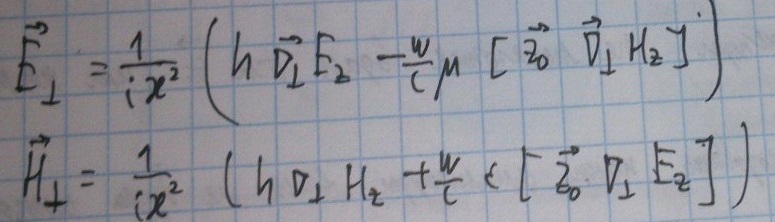
Таким образом, мы упростили себе задачу о нахождении компонент полей, т.к. вместо шести неизвестных компонент полей нам нужно найти всего две - продольные.

Теперь рассмотрим задачу:

Нахождение E_z и H_z для волновода

Для нахождения продольных компонент поля воспользуемся волновым уравнением и подставим в него ожидаемые выражения для E_z и Н_z:

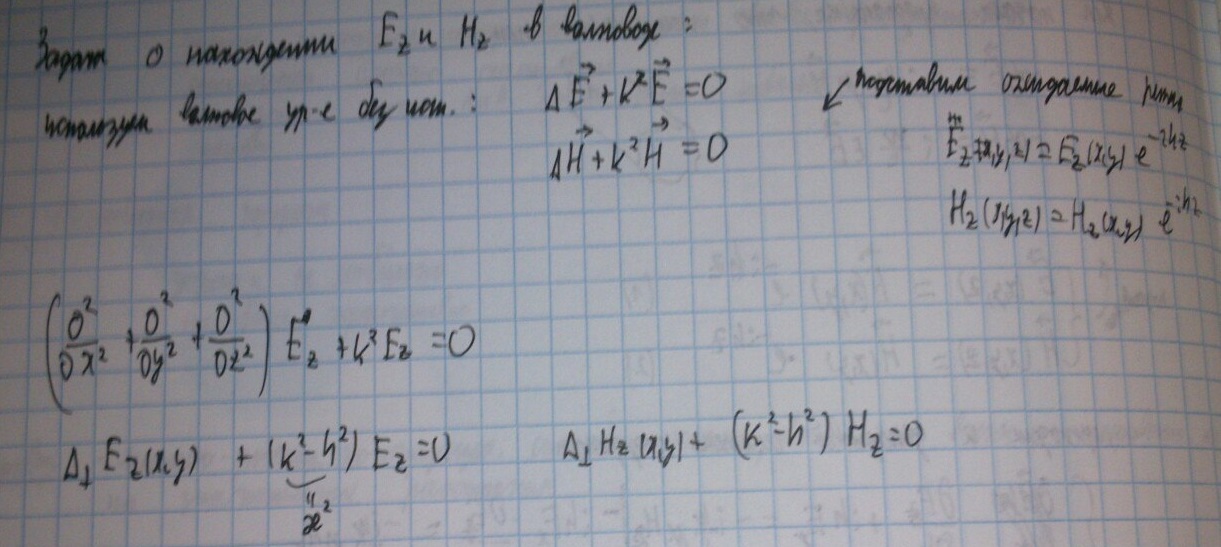
Получаем уравнения Геймгольца.

Теперь объединим полученные уравнения с граничными условиями:

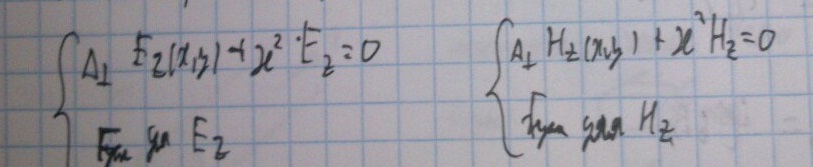
Определим эти граничные условия:

Предположим, что волновод имеет идеально проводящие стенки. При этом мы не будем учитывать вид сечения волновода.

Тангенциальные компоненты электрического поля на поверхности идеального проводника равны 0

Введем локальную систему координат для того, чтобы получить граничные условия для магнитного поля:

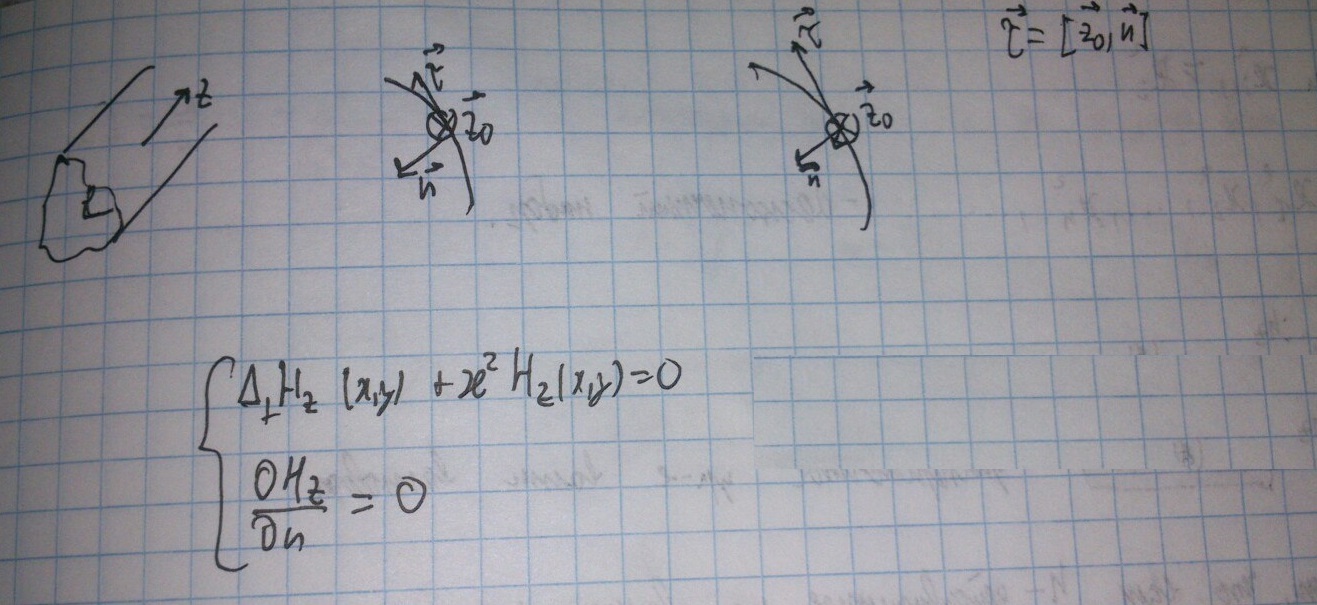
Последнее выражение получается из представления первого граничного условия во введённой системе координат: