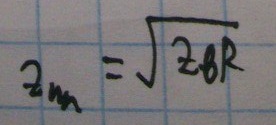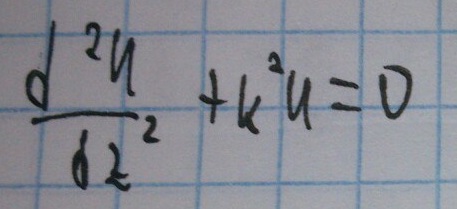
Рассмотрим телеграфное уравнение.
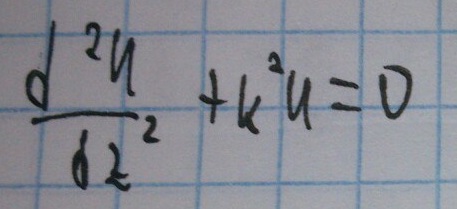
Его решение:
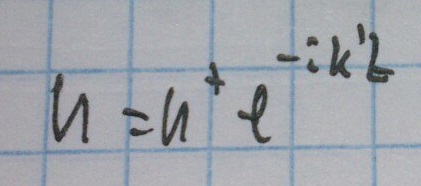
(знак "+" над множителем означает, что это волна, бегущая в положительном направлении, а знак "-" — в отрицательном)
Будем работать с волной, бегущей в + направлении.
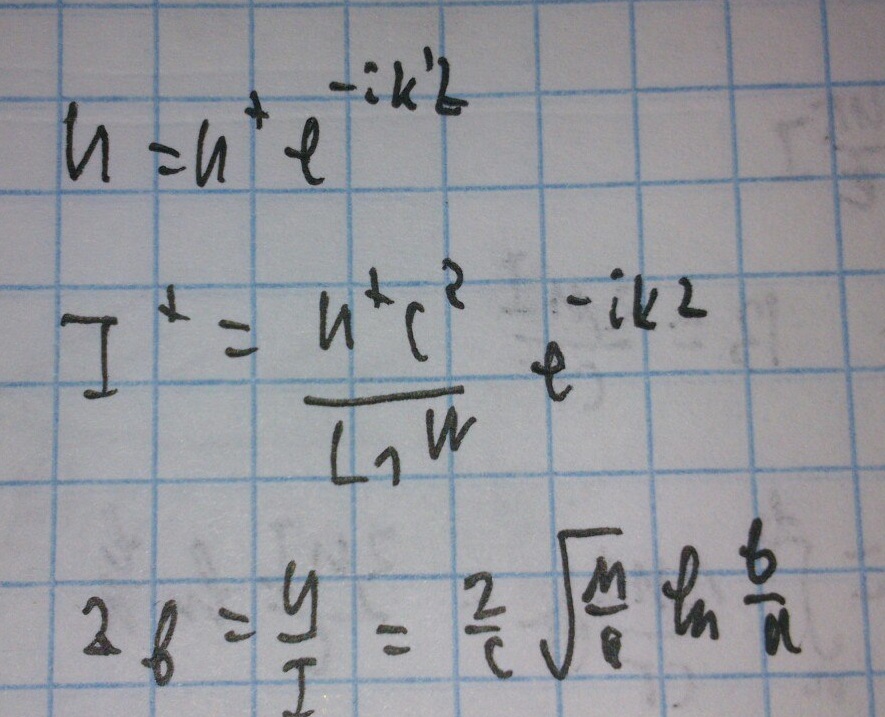— волновое сопротивление линии в бегущей волне.
Рассмотрим коаксиальную линию, в которой распространяется TM-волна.
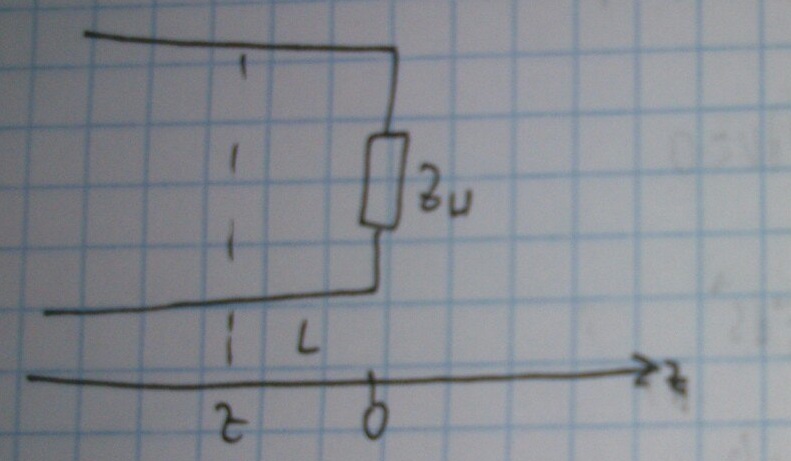
Запишем уравнения тока и напряжения в ней:
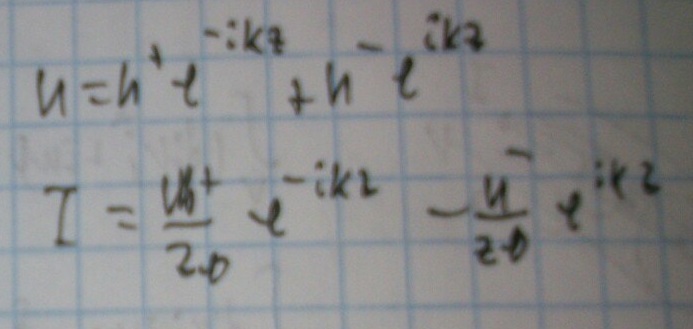
Введём вспомогательную величину:
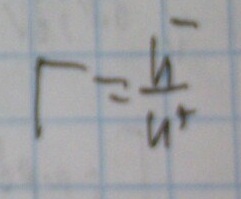— коэффициент отражения
Коэффициент отражения по напряжению — отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны в заданном сечении линии передачи.
Коэффициент отражения по току — отношение комплексной амплитуды тока отраженной волны к комплексной амплитуде тока падающей волны в заданном сечении линии передачи.
Определим импеданс в сечении:
Теперь воспользуемся граничным условием:
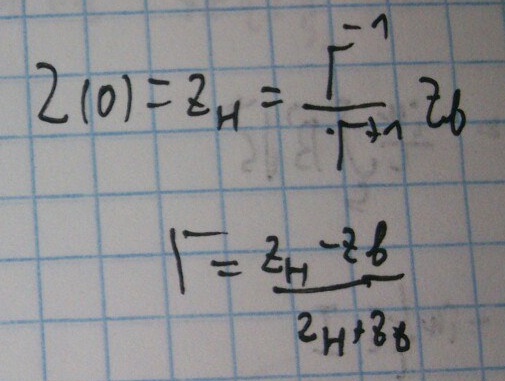
Чтобы найти импеданс в произвольном сечении, подставим Г в исходную формулу и преобразуем выражение.
В итоге получим:
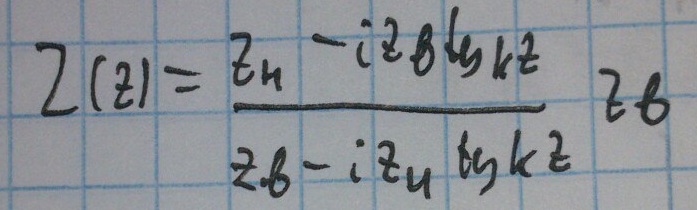
Это формула пересчета импедансов.
В случае, если рассматриваем импеданс на расстоянии L от нагрузки:
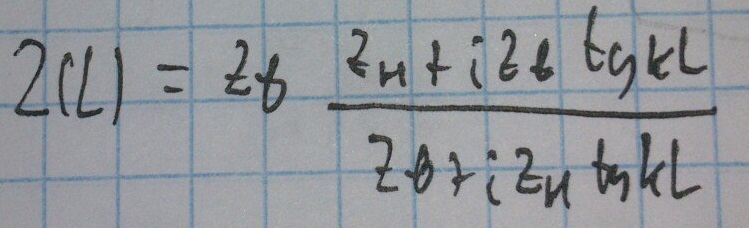
Исследуются, когда Zн равен различным предельным случаям.
1. Режим согласования.
В данном случае нет встречной волны, которая повышает уровень шума и уменьшает скорость переноса информации. В данном случае вся энергия поглащается нагрузкой.
2. Режим короткого замыкания.
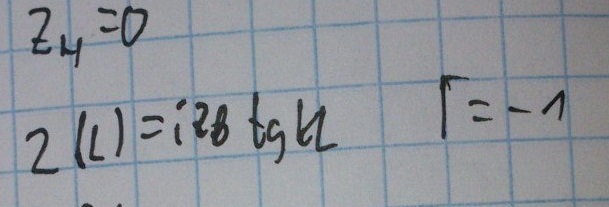
В этом режиме вся энергия отразится от нагрузки и амплитуда падающей волны равна амплитуде отраженной.
Закороченная линия позволяет получать реактивный импеданс (реактивное сопротивление - это мнимая часть импеданса):
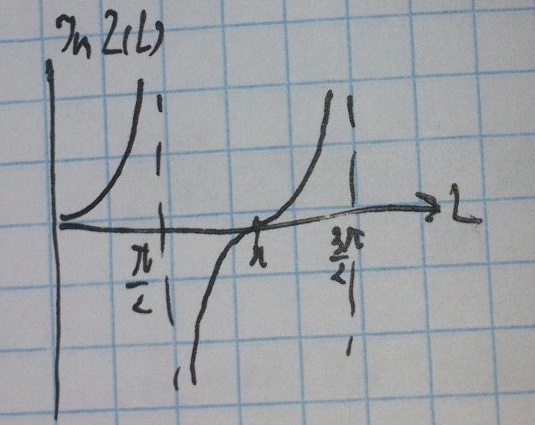
За индуктивную нагрузку отвечает положительная часть графика, за емкостную - отрицательная.
3. Режим холостого хода.
Четвертьволновой трансформатор — коаксиальная линия передачи (с одной стороны закорочена нагрузкой), длина которой равна четверти длины волны, возбуждаемой в этой линии. Часть линии выполнена из материала, который отличается от материала остальной линии.
Найдём импеданс трансформатора.
