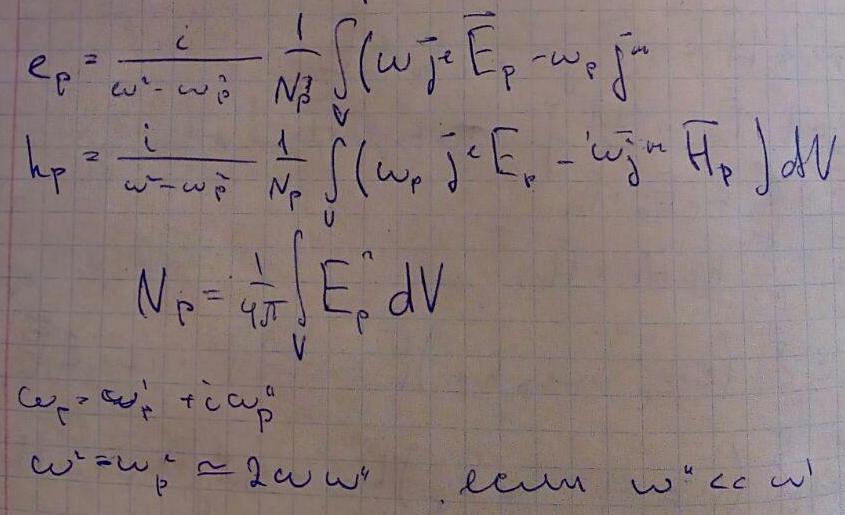
Для того, чтобы в реальном волноводе существовали электромагнитные волны, необходимо передать ему энергию, при этом нужно заметить, что поля могут возбуждаться переменными зарядами. Например, если подвести к волноводу проводник, подключенный к переменному напряжению, то появятся переменные токи внутри волновода, а следовательно появятся поля.
Наша задача состоит в том, чтобы найти поля, возбуждаемые заданными токами в волноводе. Поля, которые возбуждаются заданными источниками - это сумма мод волн. Рассмотрим поля, возбуждаемые на заданных частотах. Для этого потребуется вспомогательноое соотношение, так как в волноводе существует конечное число распространяющихся мод, следовательно их сумма будет тоже конечной. Таким вспомогательным соотношением является Лемма лоренца.
Рассмотрим в общем случае неоднородное пространство, в котором заданы два распределения тока и соответствующих им распределения поля.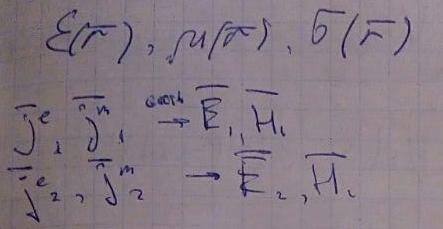
Запишем уравнения Максвелла, в которые входят электрические и магнитные токи. Далее скалярно умножим их на соответствующие поля и просуммируем все полученные выражения.
Воспользуемся формулой векторного анализа
Получим лемму Лоренца в дифференциальной форме: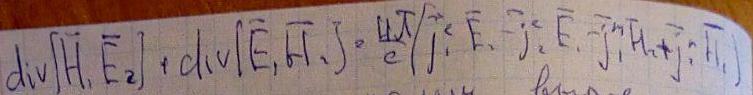
Проинтегрируем полученное выражение по произвольному V-объему, ограниченному поверхностью S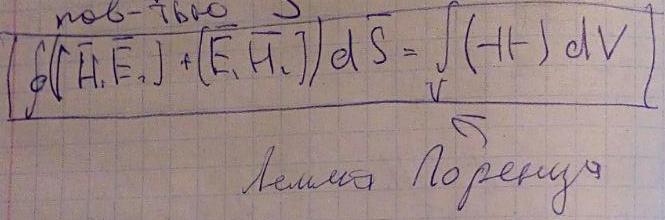
Данная лемма утверждает, что существует связь между токами и соответствующими ими полями. Можно попробовать найти распределение в какой-либо среде. Тогда, зная одно распределение, можно использовать эту связь, чтобы найти второе. Логично утверждать, что существует регулярный метод, позволяющий по одному распределению найти другие распределения.
Рассмотрим произвольный волновод с идеально-проводящими стенками, в котором заданы соответствующие распределения, локализованные в определенной точке пространства. Из физических соображений справа набор мод, бегущих вправо, слева набор мод, бегущих влево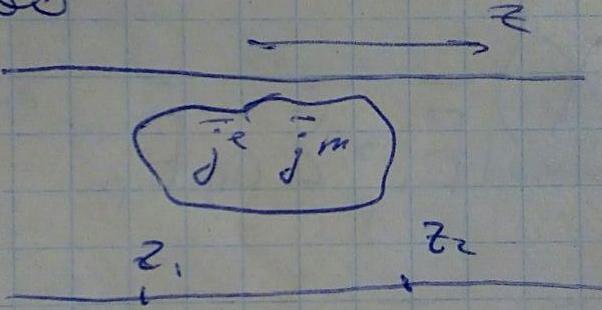
Так как волновод произвольный, обозначим моды через индекс p. Соответственно существуют поля, которые можно записать в виде: 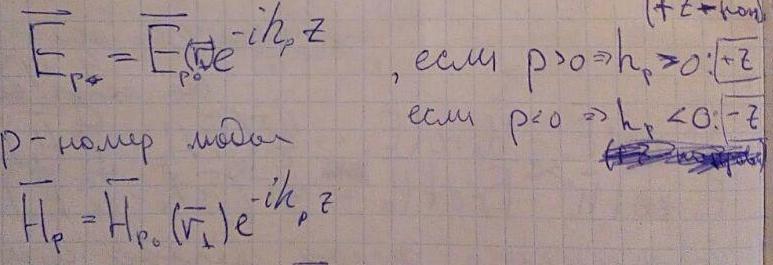
Соответственно, можно представить разложение поля по собственным модам:
Докажем это соотношение с помощью леммы Лоренца. Рассмотрим пустой волновод без источников, две моды в данном объеме и применим лемму Лоренца к полям, распространяющимся в данном объеме.
n - нормаль к поверхности. Поверхность состоит из трех составляющих: S1, S2 и боковой поверхности. Граничные условия на боковой поверхности имеют вид: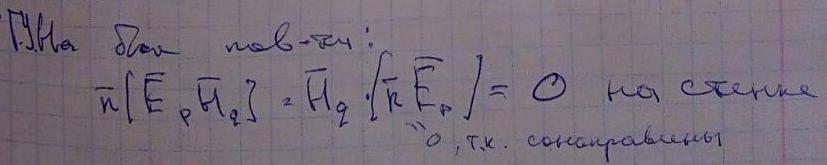
Значит интеграл по боковой поверхности равен 0, следовательно получится выражение:
Поверхности S1 и S2 были выбраны произвольно. Следовательно, Ipq не зависит от z. Изучим этот интеграл, который можно представить и в другой форме.
Теперь рассмотрим поля, возбуждаемые справа от источника. 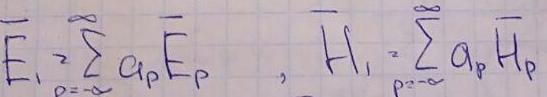
Запишем лемму Лоренца для выделенного объема для следующего случая: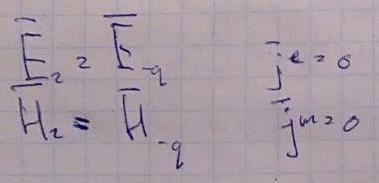
Т.е. рассмотрим в качестве вспомогательной моды поле моды, бегущей влево. Берем эталонное поле, пускаем его влево, и ищем поле бегущее вправо. С помощью замены порядков суммирования и интегрирования достанем ту, которая нам больше нужна.
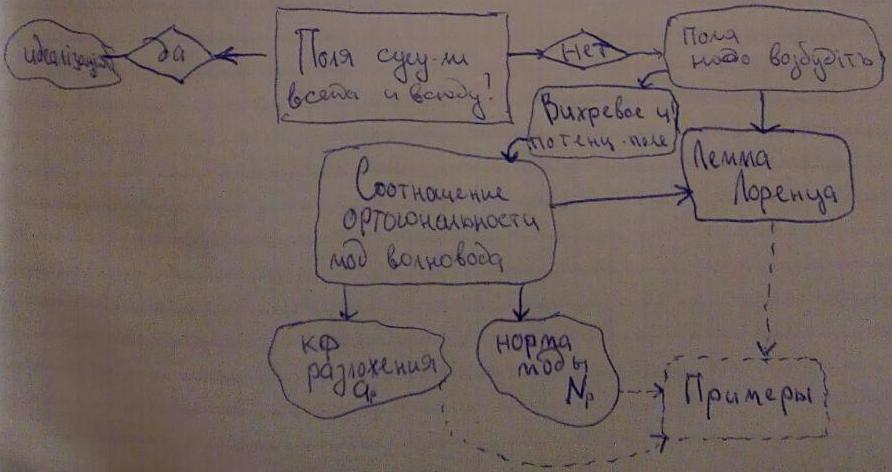
В резонаторах кроме вихревых полей создаваемых источниками могут быть потенциальные поля. Суммарное поле представляет собой сумму потенциального и вихревого поля, но потенциальные поля не представляют особого интереса.
Рассмотрим замкнутую поверхность с токами внутри: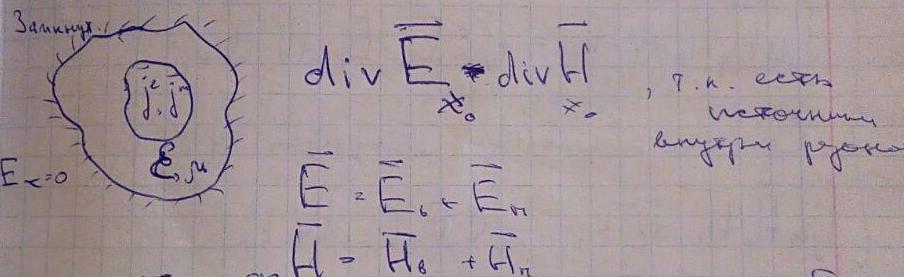
где Ев и Нв вихревое электрическое и вихревое магнитное поля, соответственно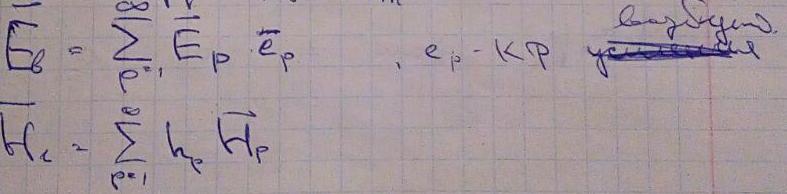
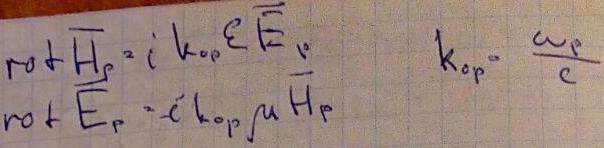
Соотношение ортогональности мод: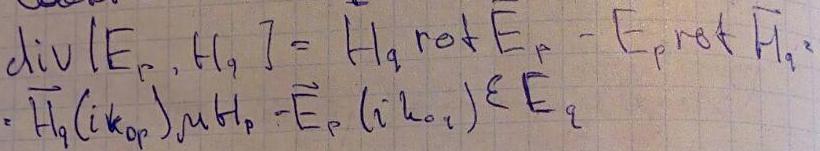
Проинтегрируем левую и правую части по объему
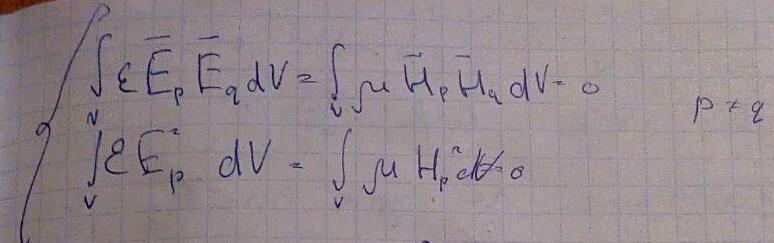
Теперь нужно записать уравнения Максвелла для искомых полей и подставить туда полученные выражения Е и Н

Домножим первое уравнение на Еq, а второе на Hp, и воспользуемся свойством ортогональности мод. Тогда, благодаря свойству ортогональности: