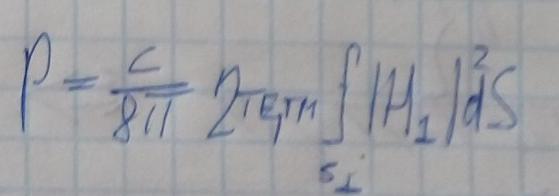

Учтём граничные условия для магнитного поля и составим для него систему уравнений.
Первое уравнение системы написано для E-волн, второе — для ТМ-волн.
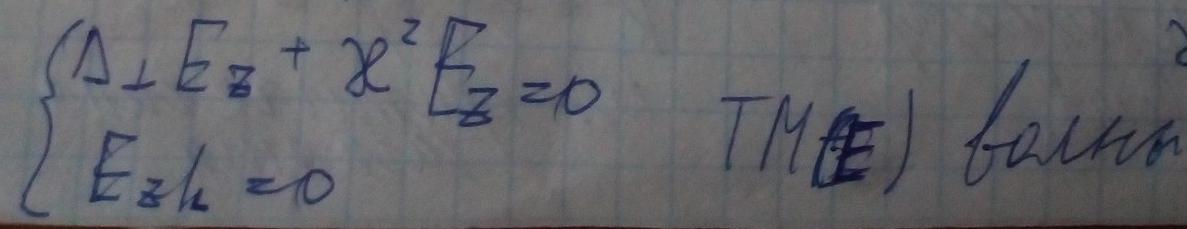
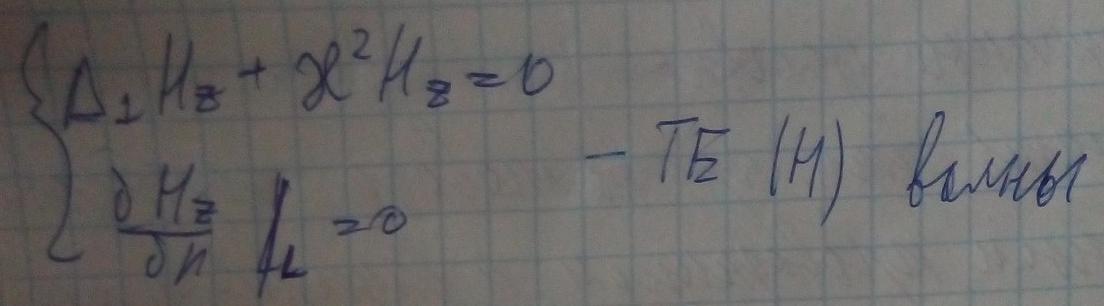
В результате получили две краевые задачи, которые независимы друг от друга, следовательно в волноводе существует два типа независимых волн.
1. E волна или TM волна, магнитное поле в которой поперечное;
2. H волна или TE волна, электрическое поле в которой поперечное.
Также существует тип волны, в которой присутствуют как поперечные, так и продольные составляющие полей - TEM волна.
Первый множитель в первом слагаемом первого уравнения является двумерным оператором Лапласа.
Решение данных задач возможно при конкретных собственных числах, являющихся попречными волновыми числами, а решения соответствующие данным собственным числам носят название собственных функций.
Конкретный вид границы будет определять собственные числа краевой задачи.
Это означает, что решение задач производится не при произвольном каппа, а при заданном
Форма границы будет определять собственные числа краевой задачи.
Для 1 и 2 задач собственные числа можно обьединить в набор положительных собственных чисел(бесконечный).
Пока рассматриваем каппа не равное 0.
Каппа - число, определяемое только формой поперечного сечения волновода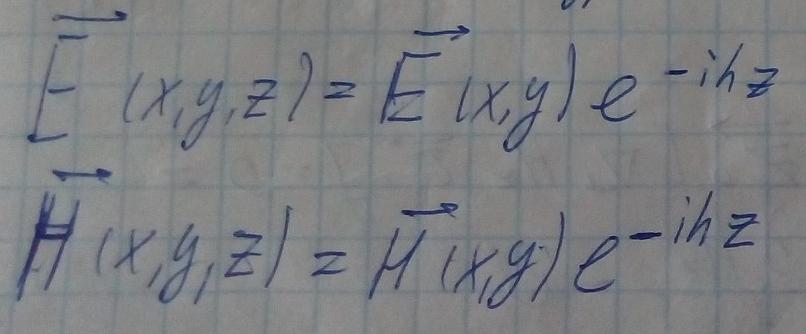
этот вид зависимости показывает, что если h — действительное, то волна является распространяющейся, если же h — мнимая, то волна — потенциально спадающая (не распространяющаяся)..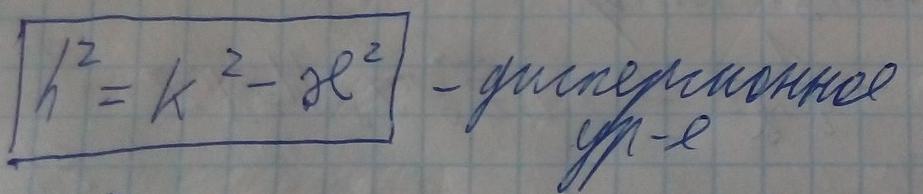
Волноводная длина волны: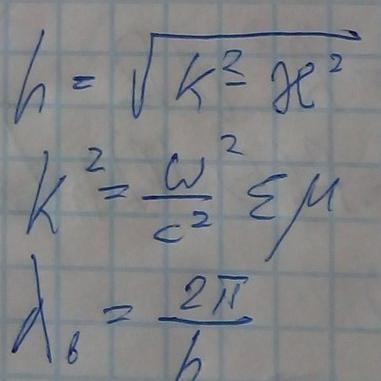
Введём вспомогательные понятия.
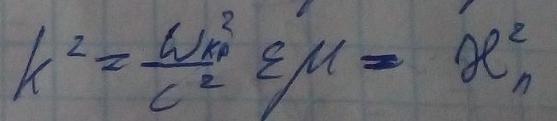

Принято выражать длину волны в волноводе на частоте ω через длину волны в свободном пространстве соответствующей заданной частоте и критическую длину волны данной моды.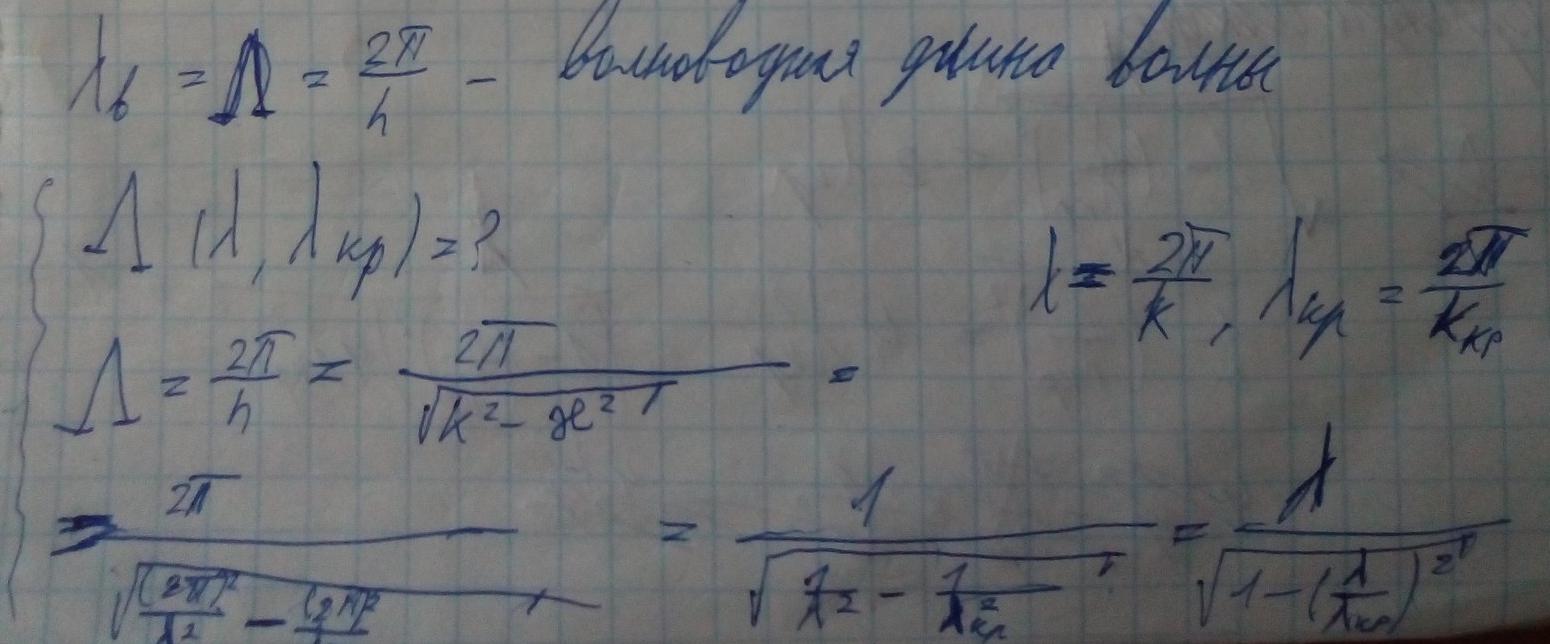
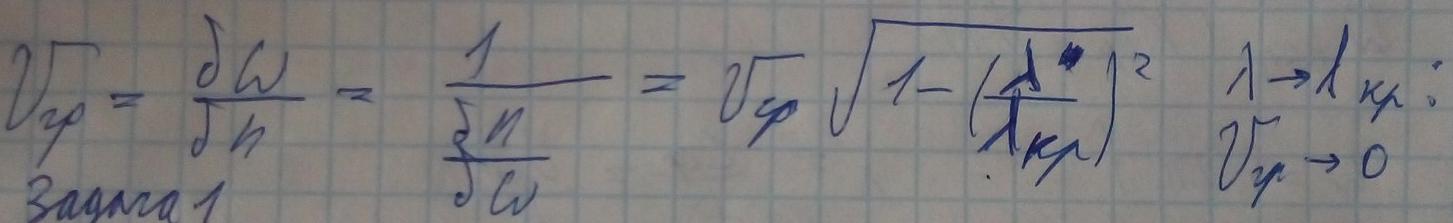
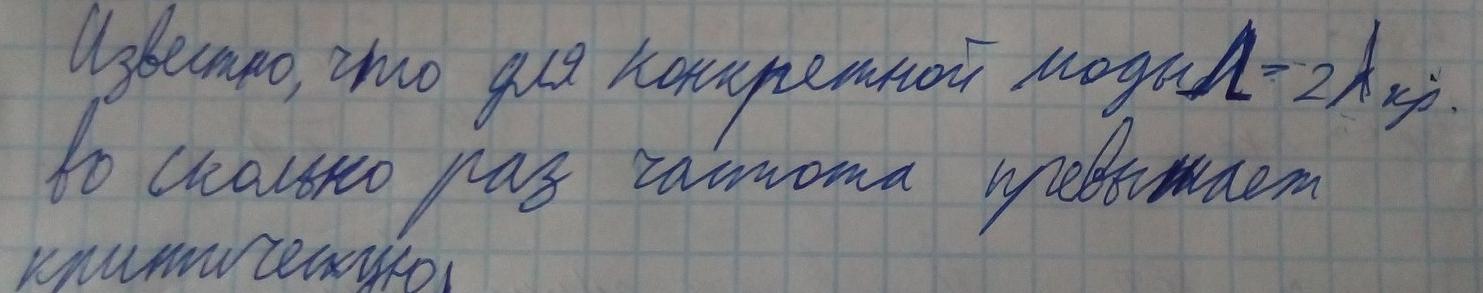
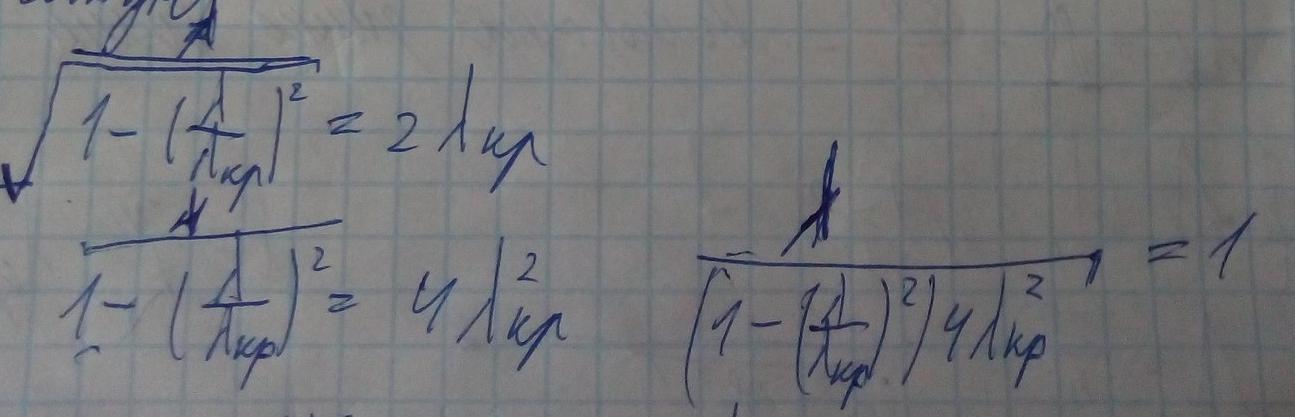

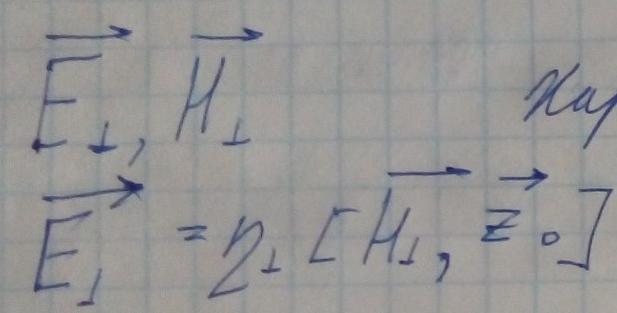
Подставим выражения E и H перпердикулярных для TE и TM волн.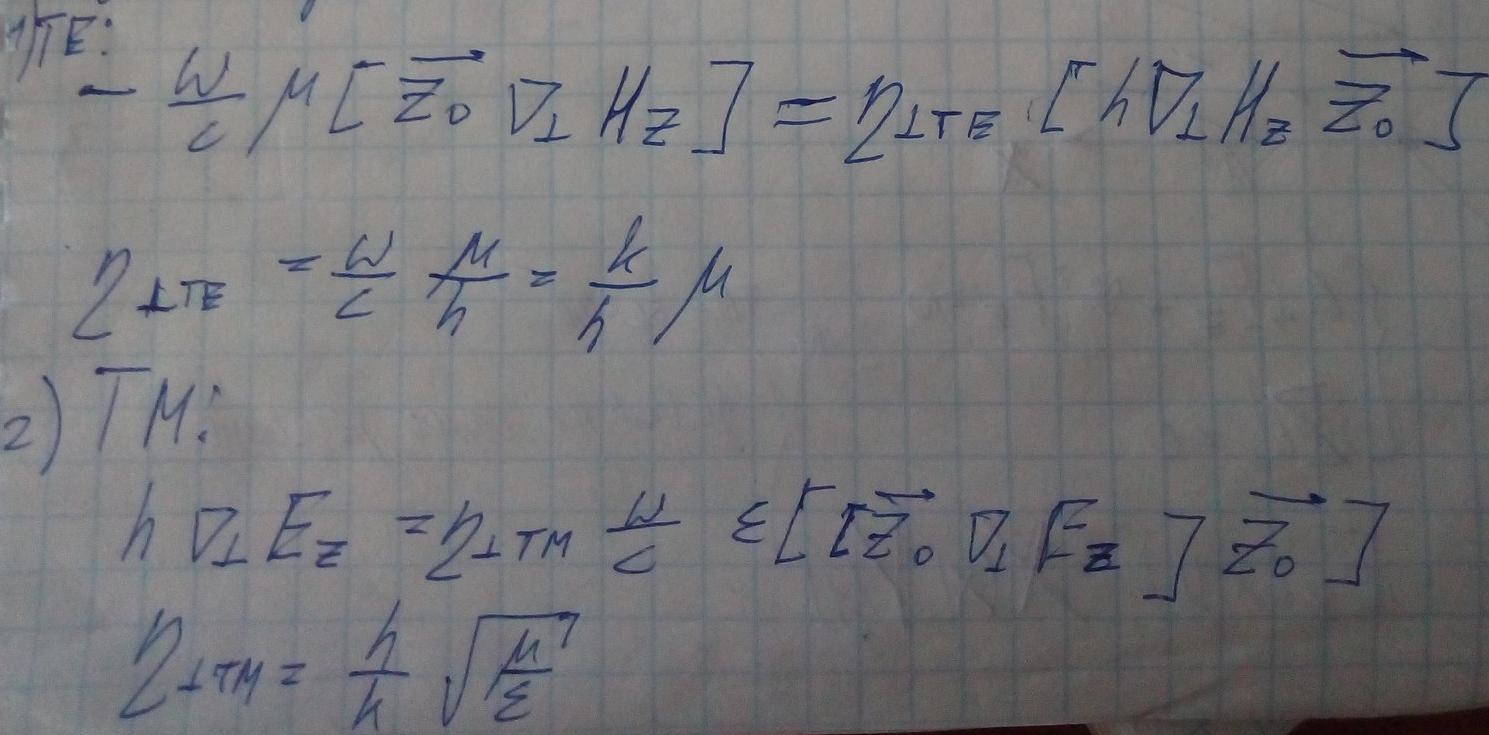
Вектор Пойтинга волноводный моды.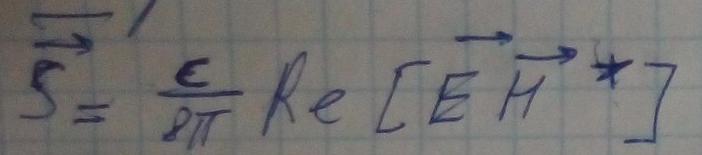
За перенос энергии вдоль волновода будут отвечать поперечные компоненты полей.
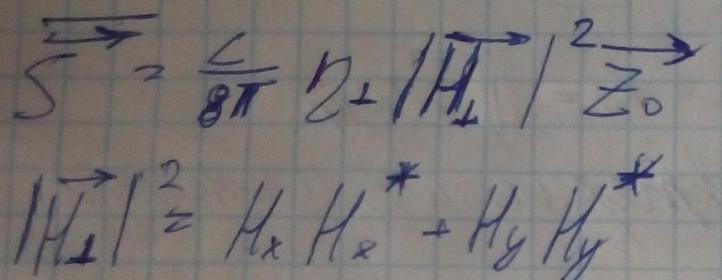
При этом переносимая волноводом мощность равна: