

Допустим есть 2 точки: А и В. Необходимо передать между ними информацию или энергию. Сделать это можно двумя подходами:
1) Без инфраструктуры 
Плюсы:
1) Между А и В не надо ничего строить (дешевизна)
2) Мобильность( А и В можно двигать)
Минусы:
1) Передаётся не вся энергия
2) Кроме полезного сигнала приходят помехи(шумы)
3) Есть риск атак
2) Волноводная передача
Плюсы:
1) Энергетическая эффективность
2) Трудно прослушать
3) Большое отношение сигнал/шум
4) Скорость передачи очень большая
Волновод - вытянутая структура, образованная металлом и диэлектриком.
По зависимости поперечного сечения от продольной координаты:
Регулярный - вытянутый вдоль оси Z металло-диэлектрическая структура, параметры которой не изменяются либо изменяются периодически вдоль этой оси.
Нерегулярный
Периодический
По наличию внешнего экрана:
Открытые - четкой границы нет. В них электромагнитное излучение проникает за стенки волновода.
Закрытые - можно четко указать границу, где заканчивается поле. В них электромагнитное излучение не проникает за стенки волновода. 
По порядку связности
Односвязные
Многосвязные
Нулевой связности(отсутствуют проводящие поверхности)
По потерям
С потерями
Без потерь
По происхождению
Природные - например, базальтовый слой(литосферный волновод)
Искусственные
Теория волноводов базируется на уравнениях Максвелла:
Рассмотрим регулярный бесконечный волновод в отсутствии источников и потерь, неизвестны 6 скалярных величин: Ex,Ey,Ez,Hx,Hy,Hz,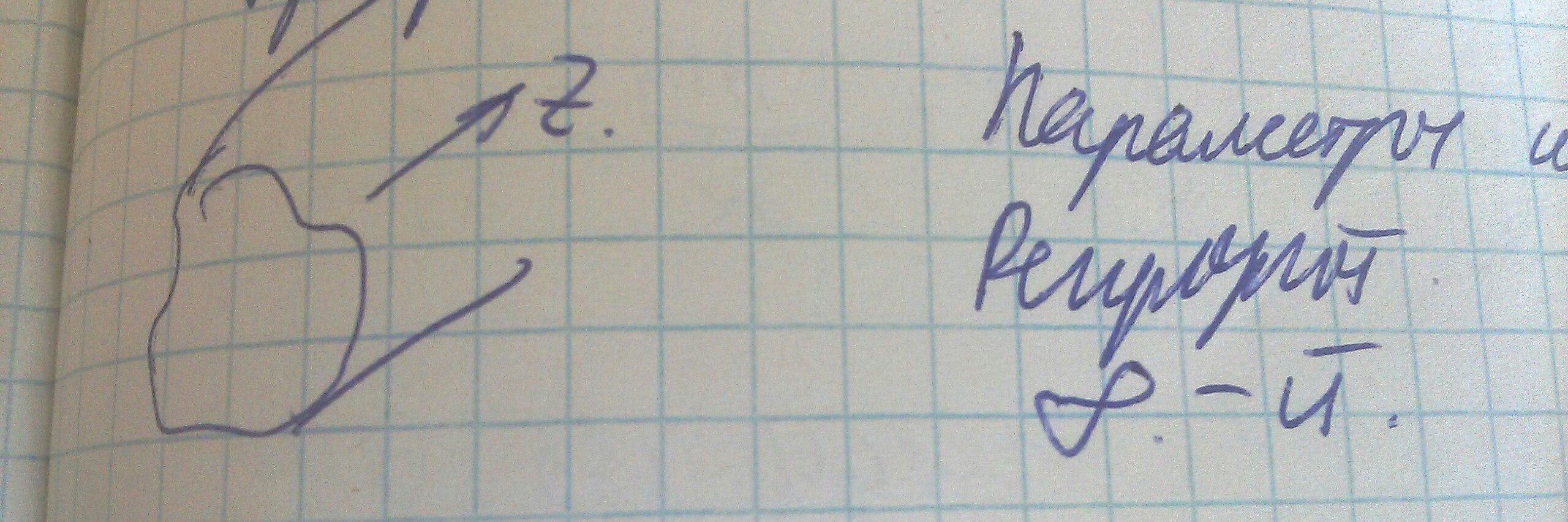
Из этих уравнений получим выражения, представляющие поперечные компоненты через производные от продольных, + выражения в векторном виде:

Из волновых уравнений, с помощью уравнения Гельмгольца найдем продольные компоненты поля:
Необходимы граничные условия(краевые задачи), найдем их для Ez и Hz
Считаем что стенки идеально проводящие, т.е тангенциальная составляющая поля Е на поверхности равна 0: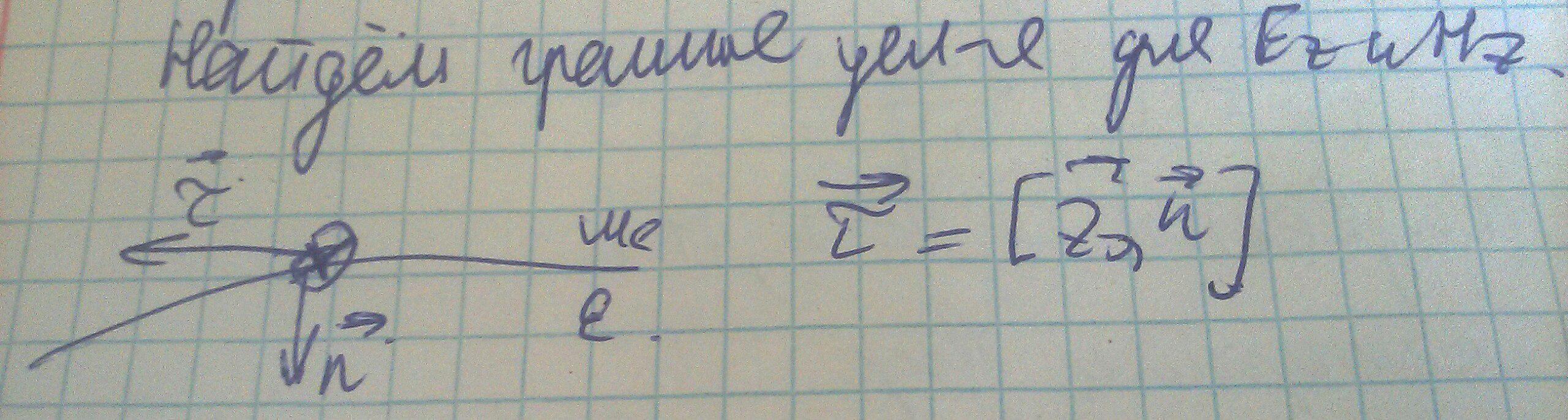
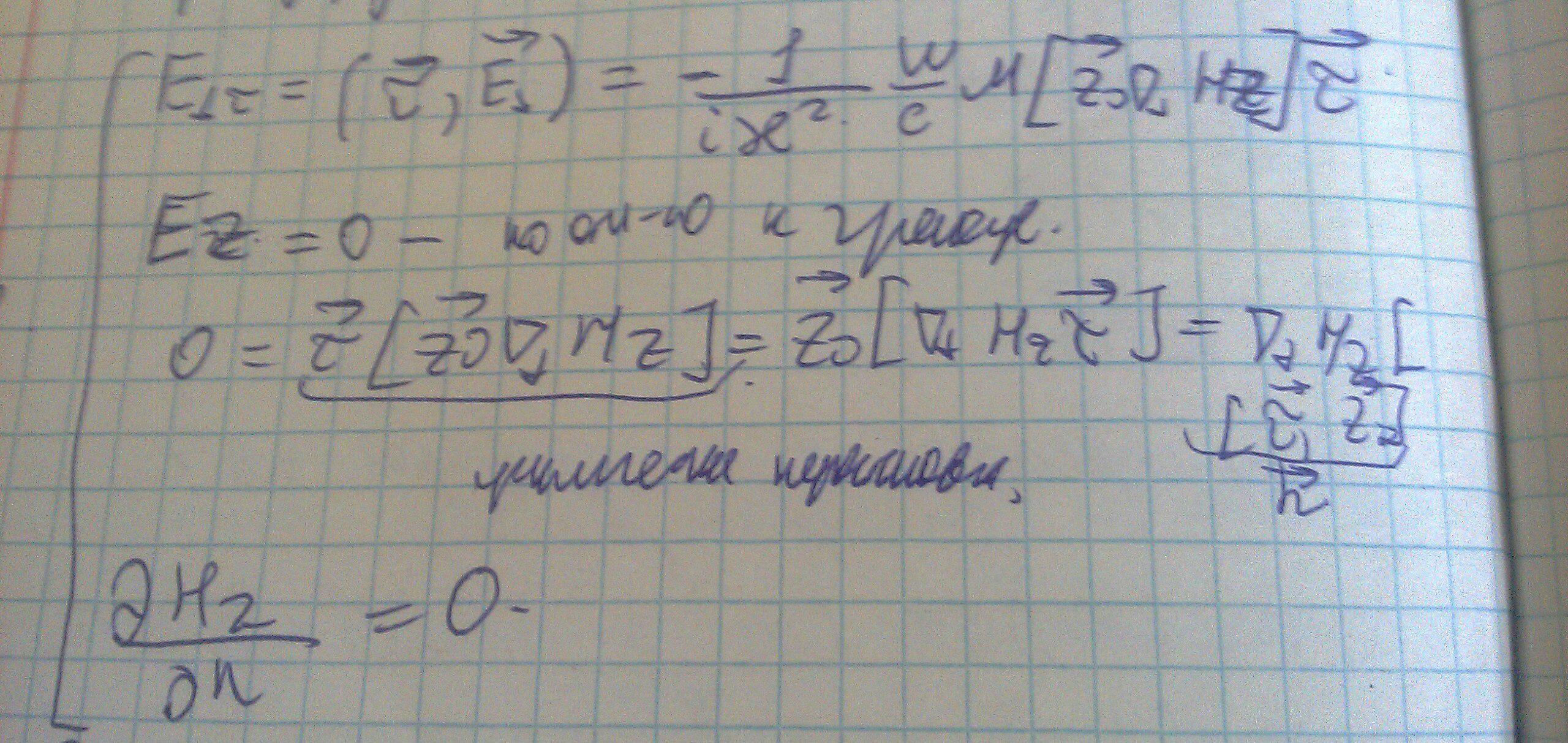
ОГЛАВЛЕНИЕ Следующая лекция>>