
Рассмотрим коаксиальную линию.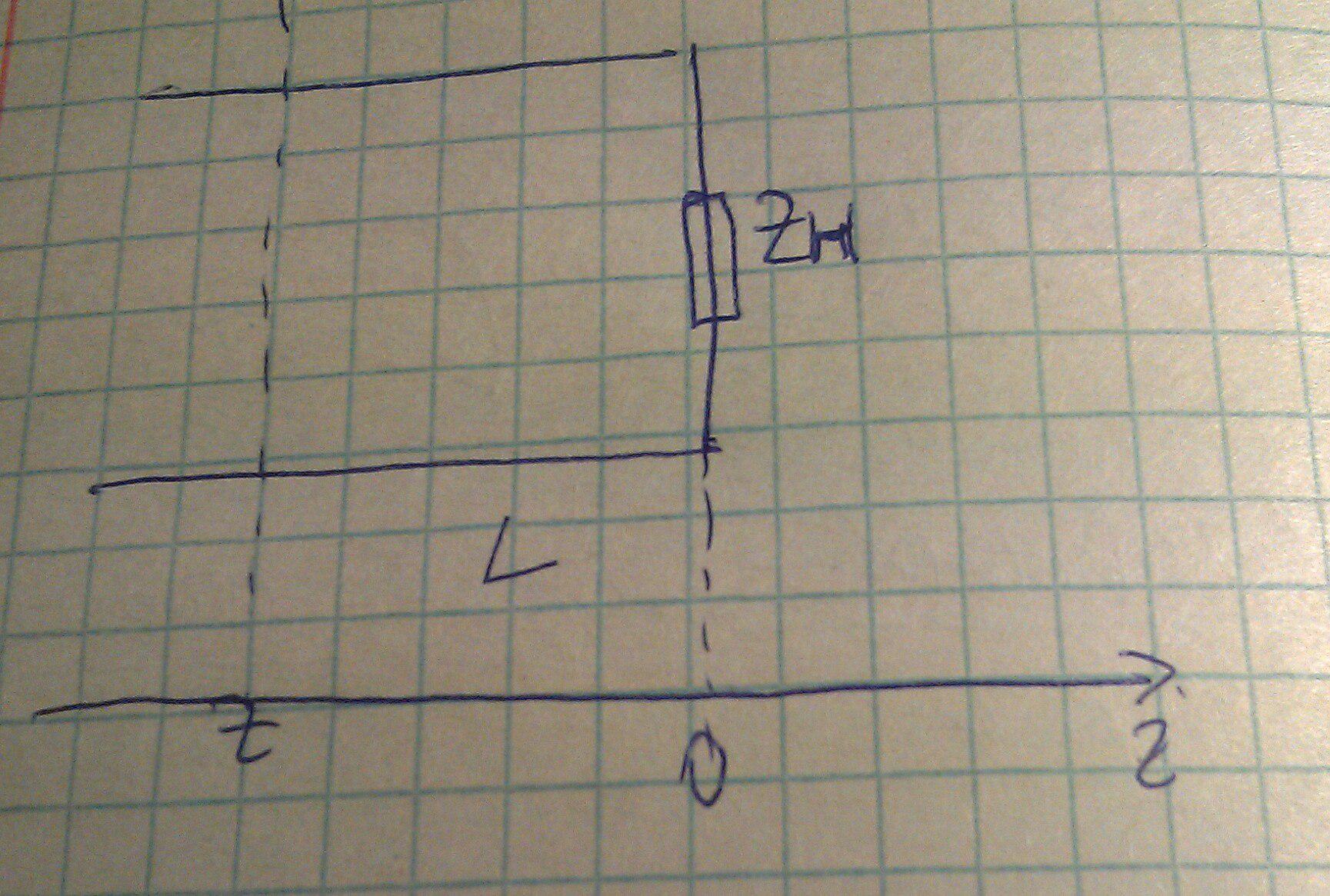
Запишем уравнения для тока и напряжения в ней.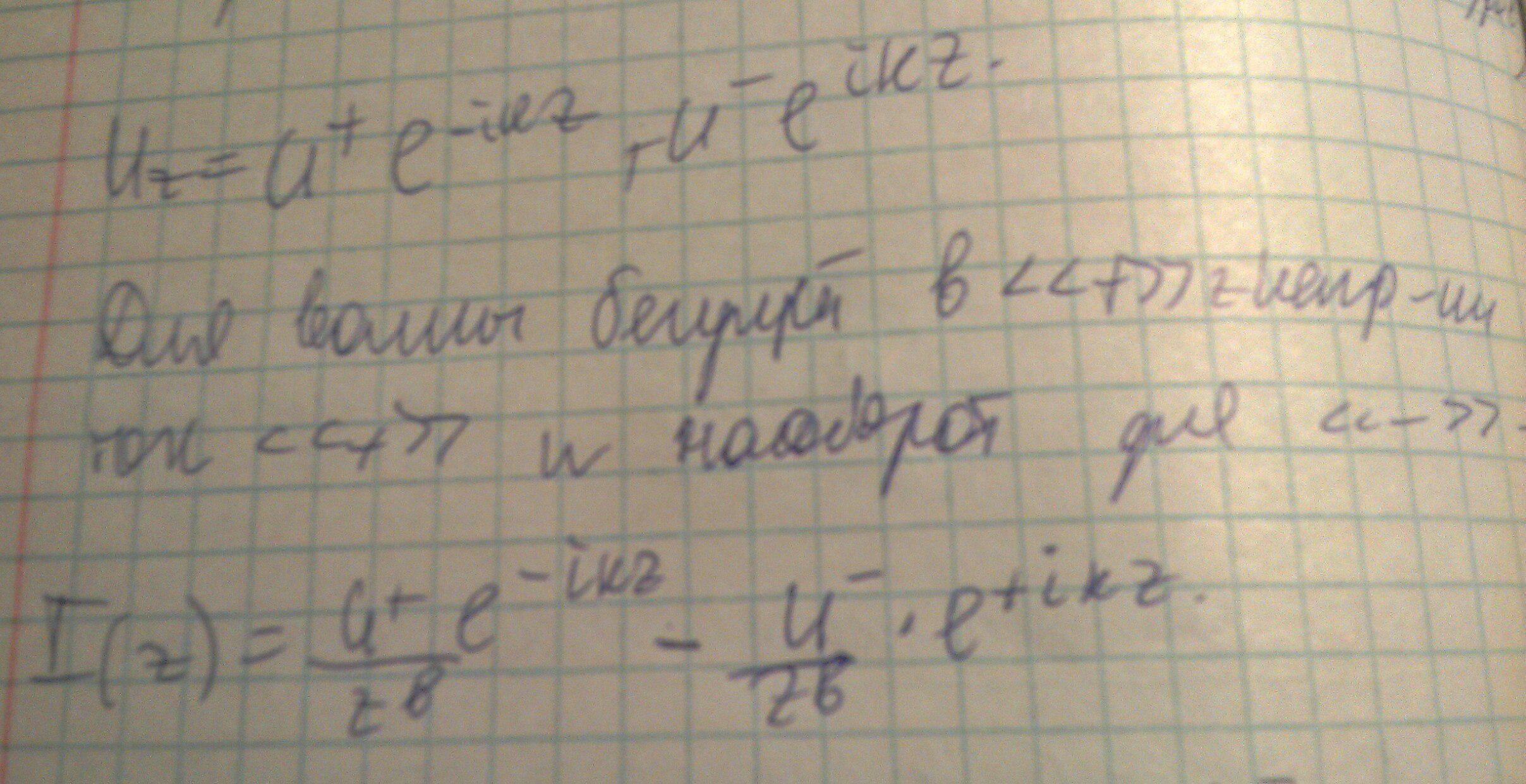
Введем вспомогательную величину, которя называется коэффициентом отражения в сечении z, равное отношению амплитуды отраженной волны, к амплитуде падающей.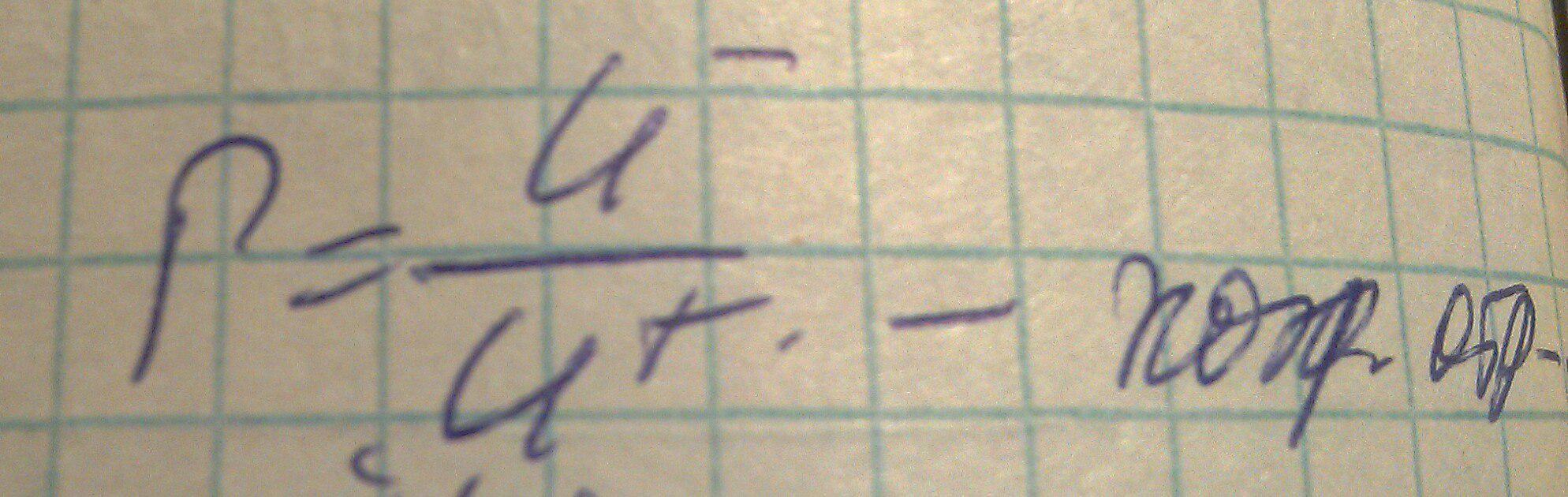
Теперь запишем выражение для импеданса в сечении: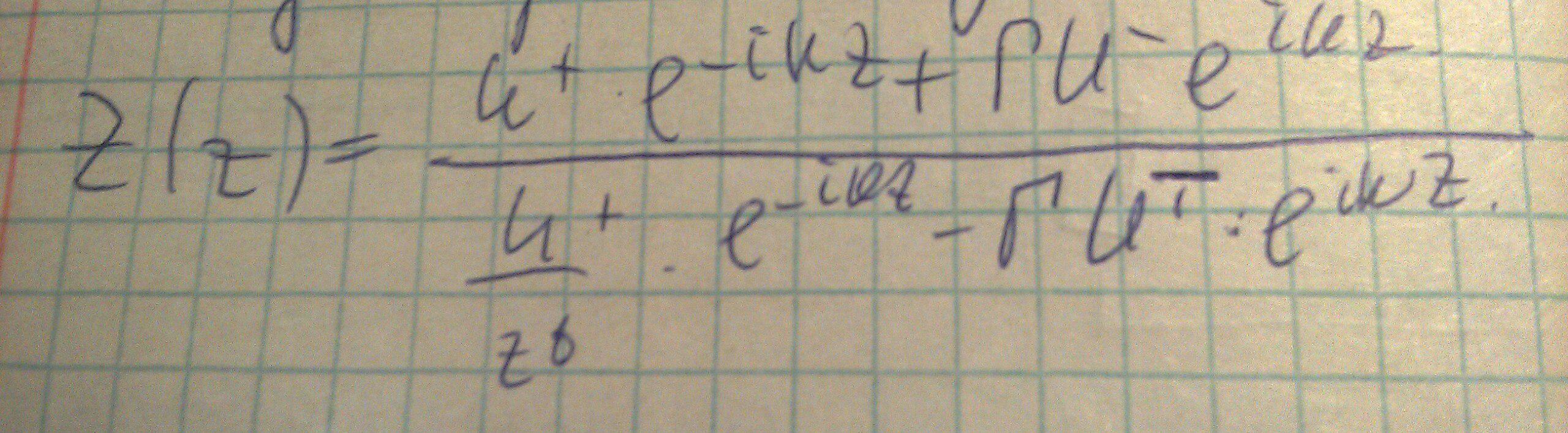
Воспользуемся граничным условием, тоесть то, что импеданс в начале координат равен импедансу нагрузки. Из него выразим коэффициент отражения, которе подставим в значение имеданса в сечении. Получим искомую формулу пересчета импедансов: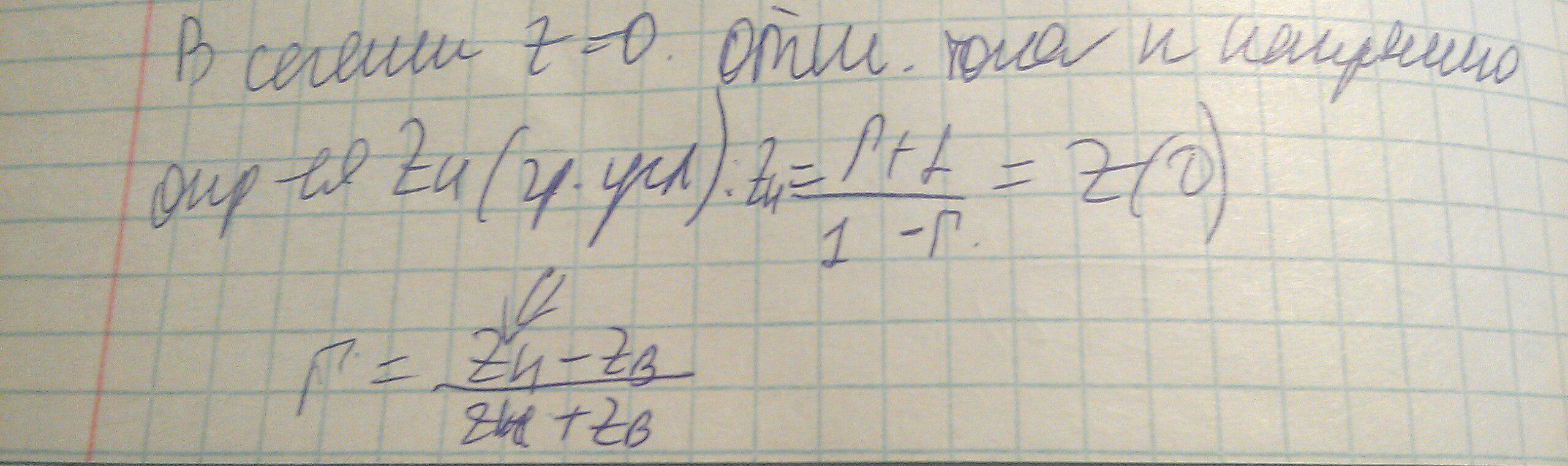

1) Режим согласования нагрузки и линии передач.
При данном режиме работы импеданс нагрузки равен волновому сопротивлению, из чего следует что коэффициент отражения равен 0. Значит в данном случае нет встречной волны, которая повышает уровень шума и уменьшает скорость переноса информации. В данном случае вся энергия поглощается нагрузкой.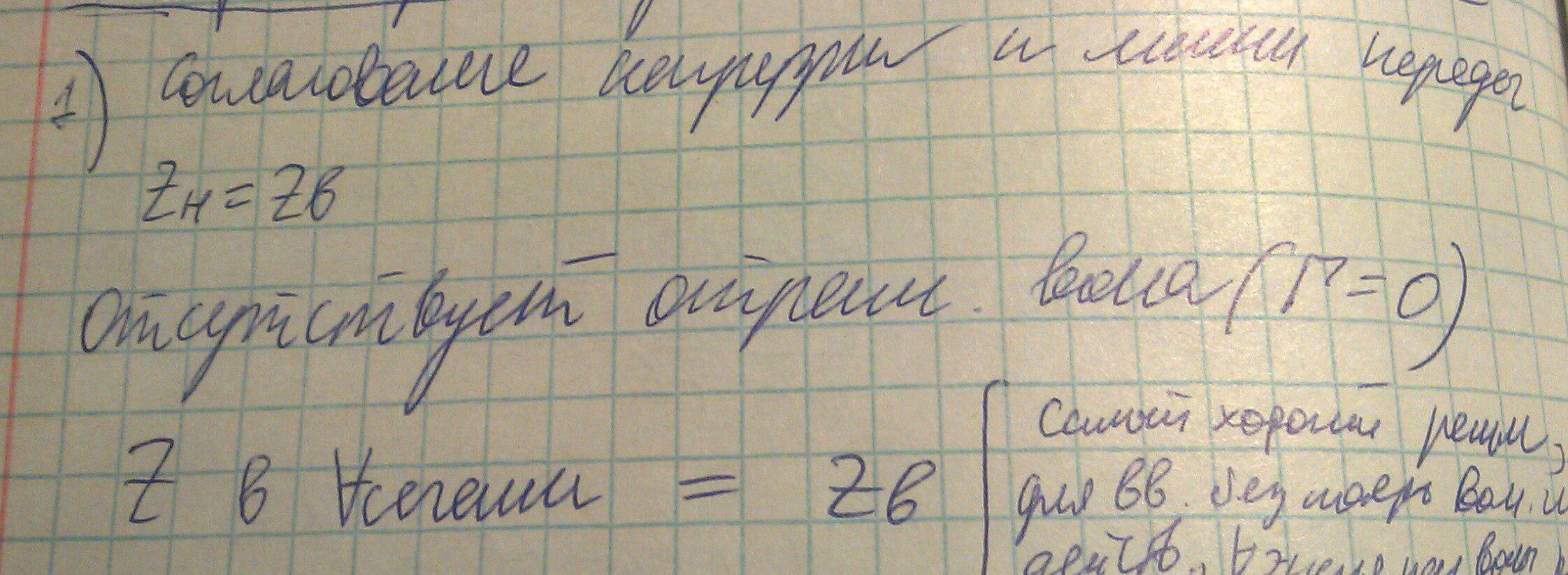
2) Режим короткого замыкания.
При данном режиме работы импеданс нагрузки равен нулю, соответственно коэффициент отражения равен минус единице, а из формулы пересчета импедансов следует: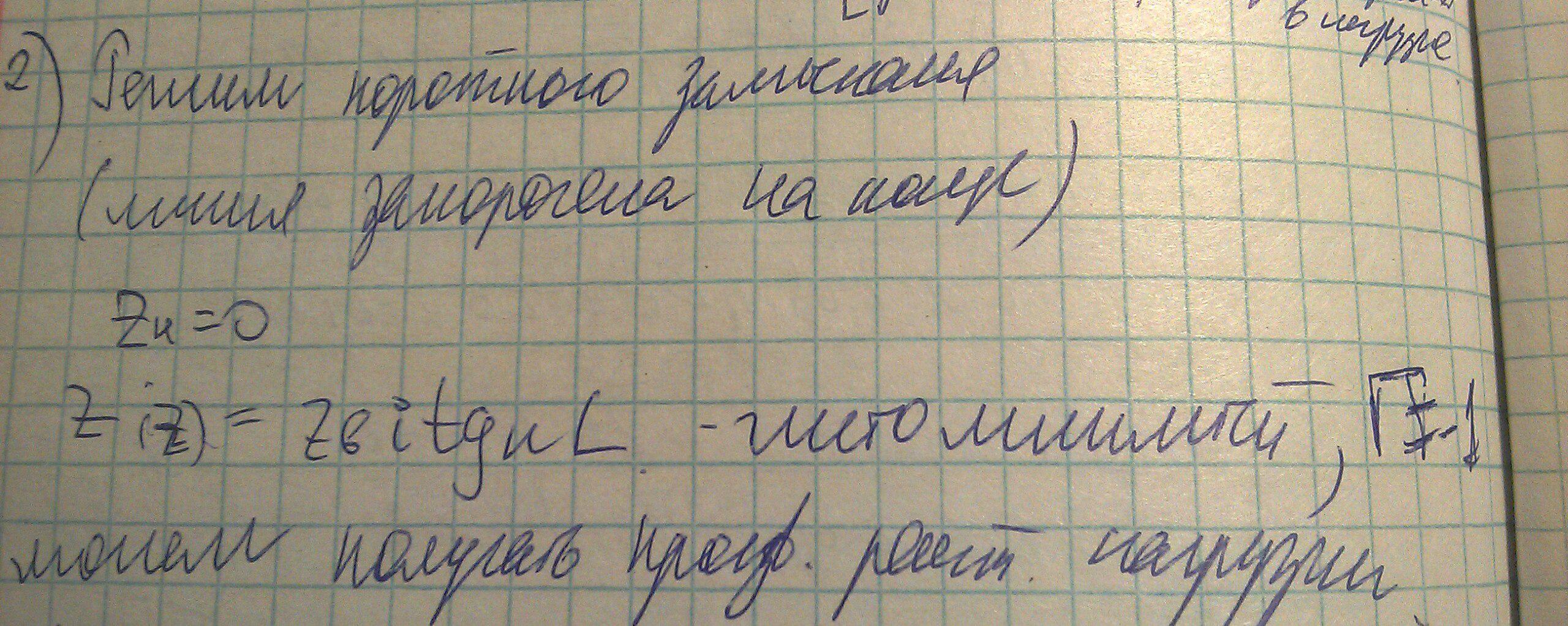
Это означает, что вся энергия отразится от нагрузки и амплитуда падающей волны равна амплитуде отраженной. Закороченная линия позволяет получать реактивный импеданс, что можно проследить по следующему графику: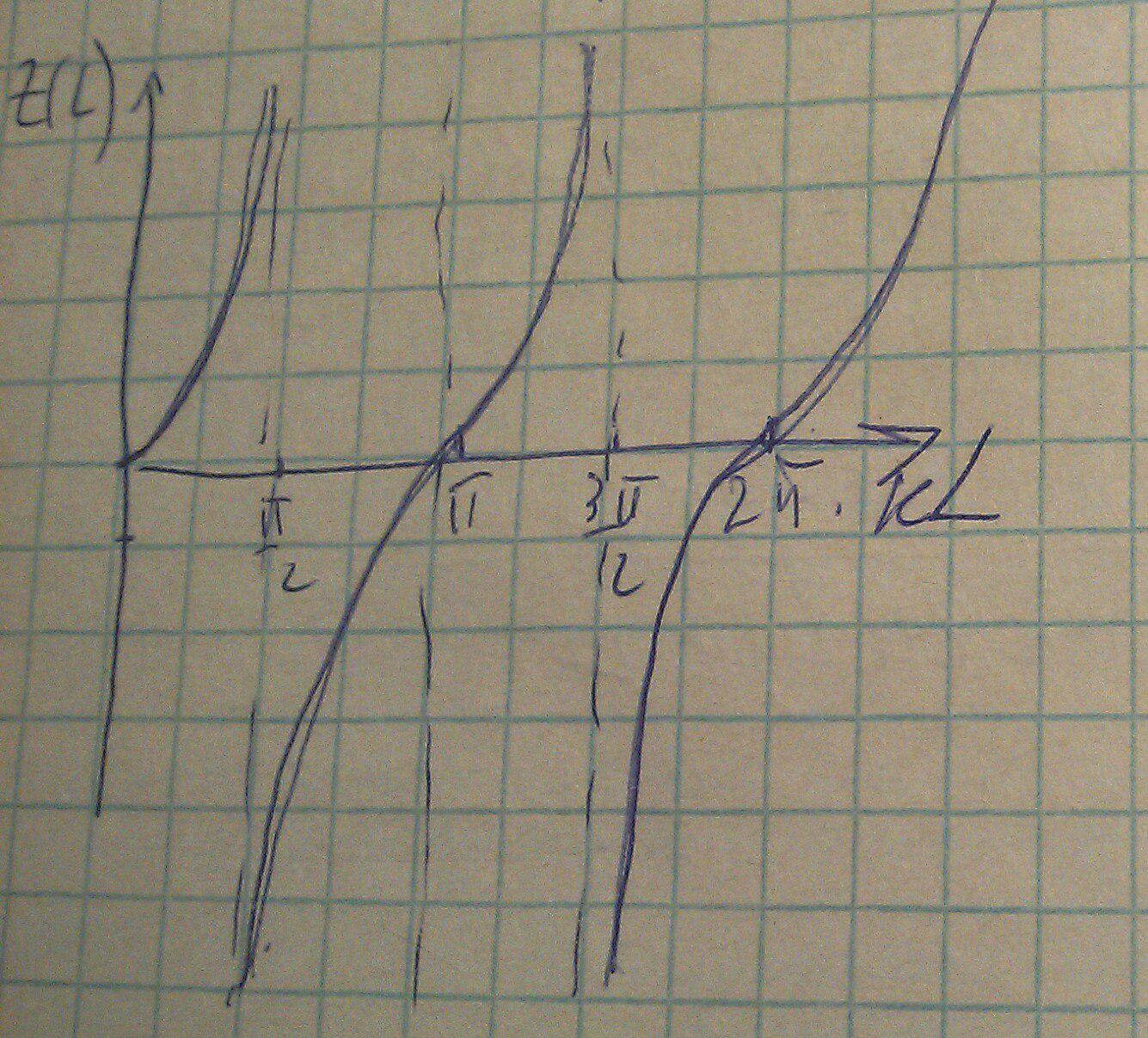
Часть графика, находящаяся выше нуля отвечает за индуктивную нагрузку, а та часть что ниже нуля за емкостную.
3) Режим холостого хода.
При данном режиме импеданс нагрузки равен бесконечности, соотвественно коэффициент отражения равен единице, а импеданс в сечении по формуле пересчета импедансов равен:
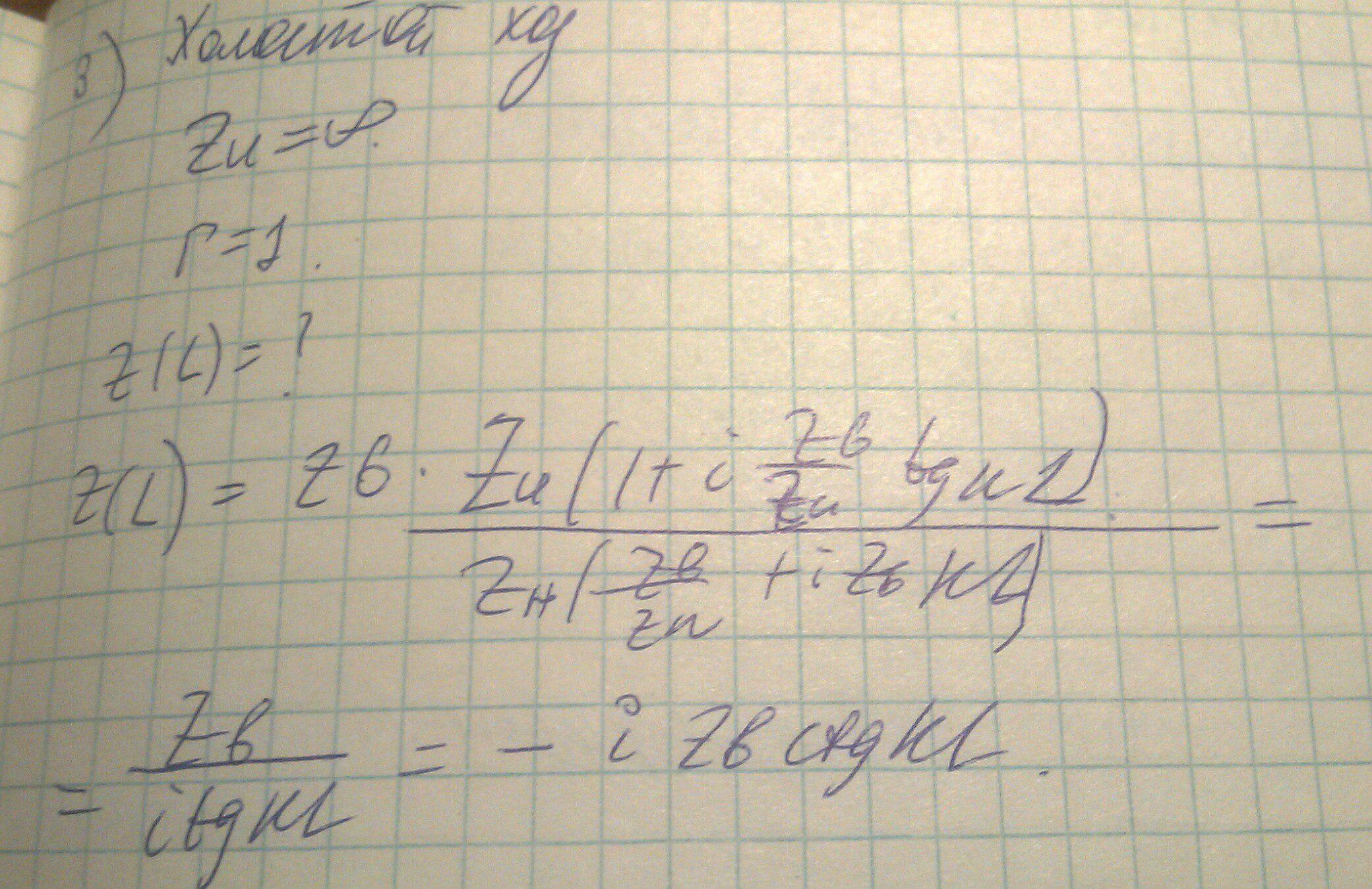
График будет иметь следующий вид: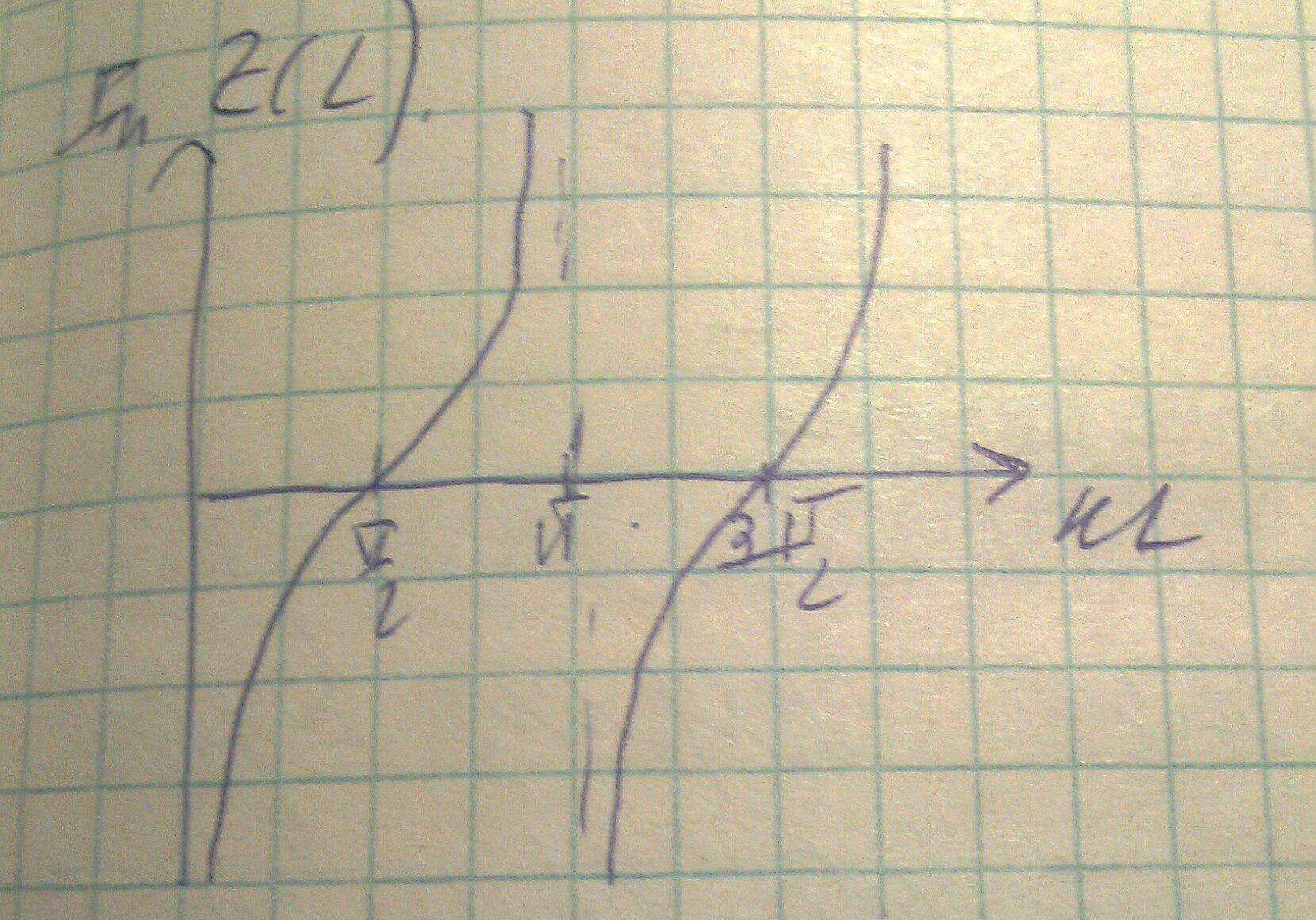
Четвертьволновой трансформатор — отрезок СВЧ линии передачи, длина которой (с учётом её коэффициента укорочения) равна четверти длины волны, возбуждаемой в этой линии.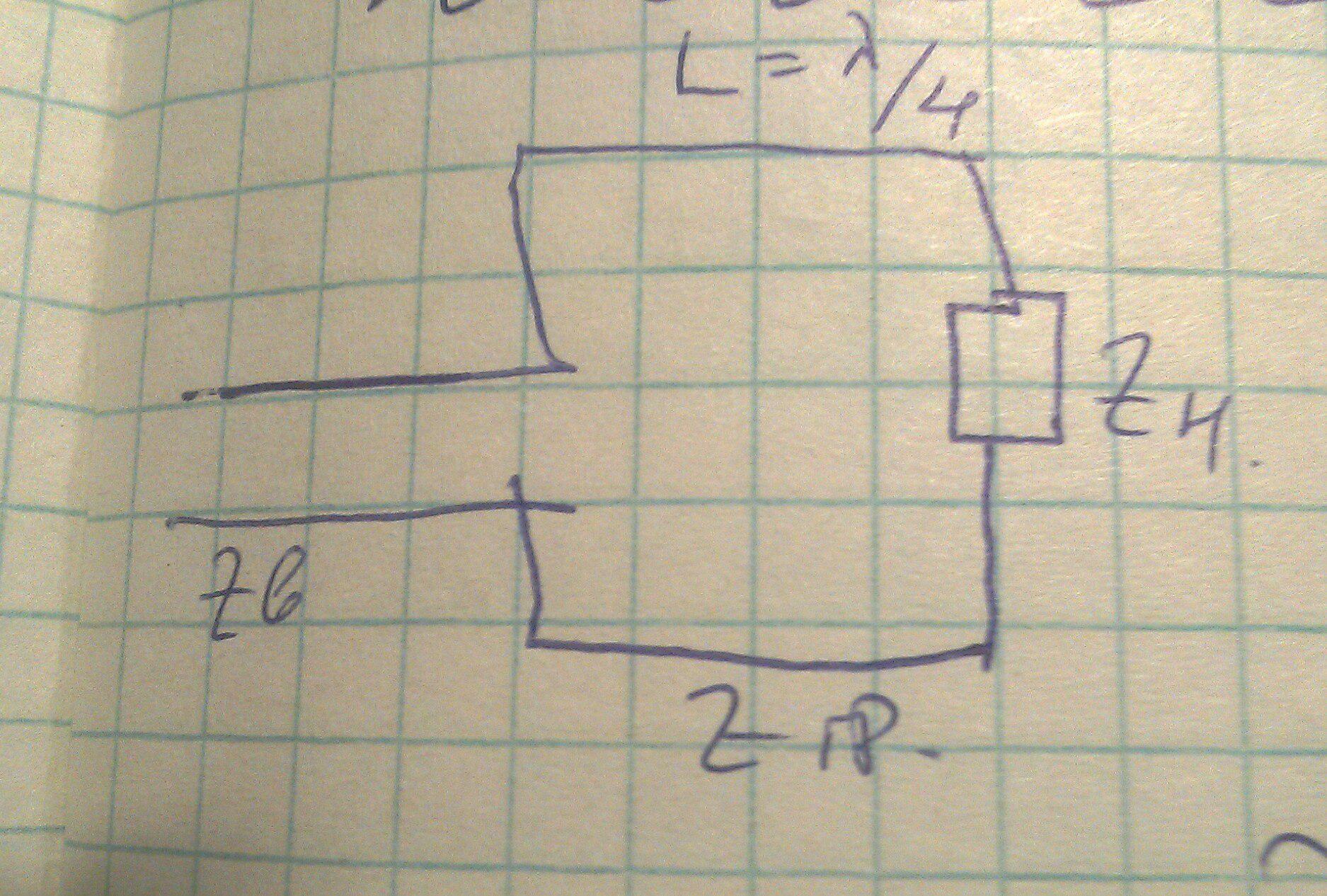
Плюсы: простой
Минусы: не перестраивает частоты, для этого используют -1- и -2- шлейфовые трансформаторы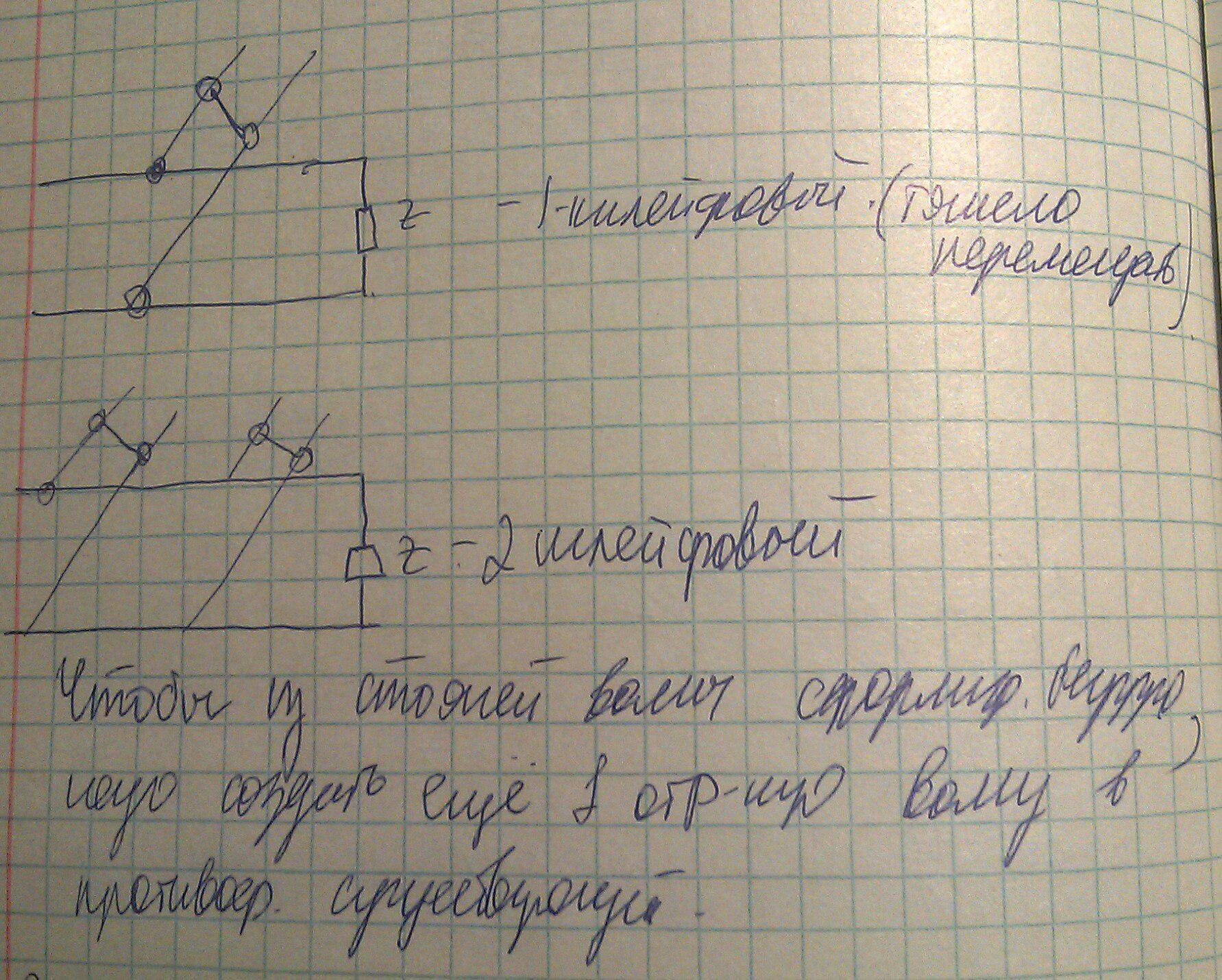
Найдём импеданс трансформатора.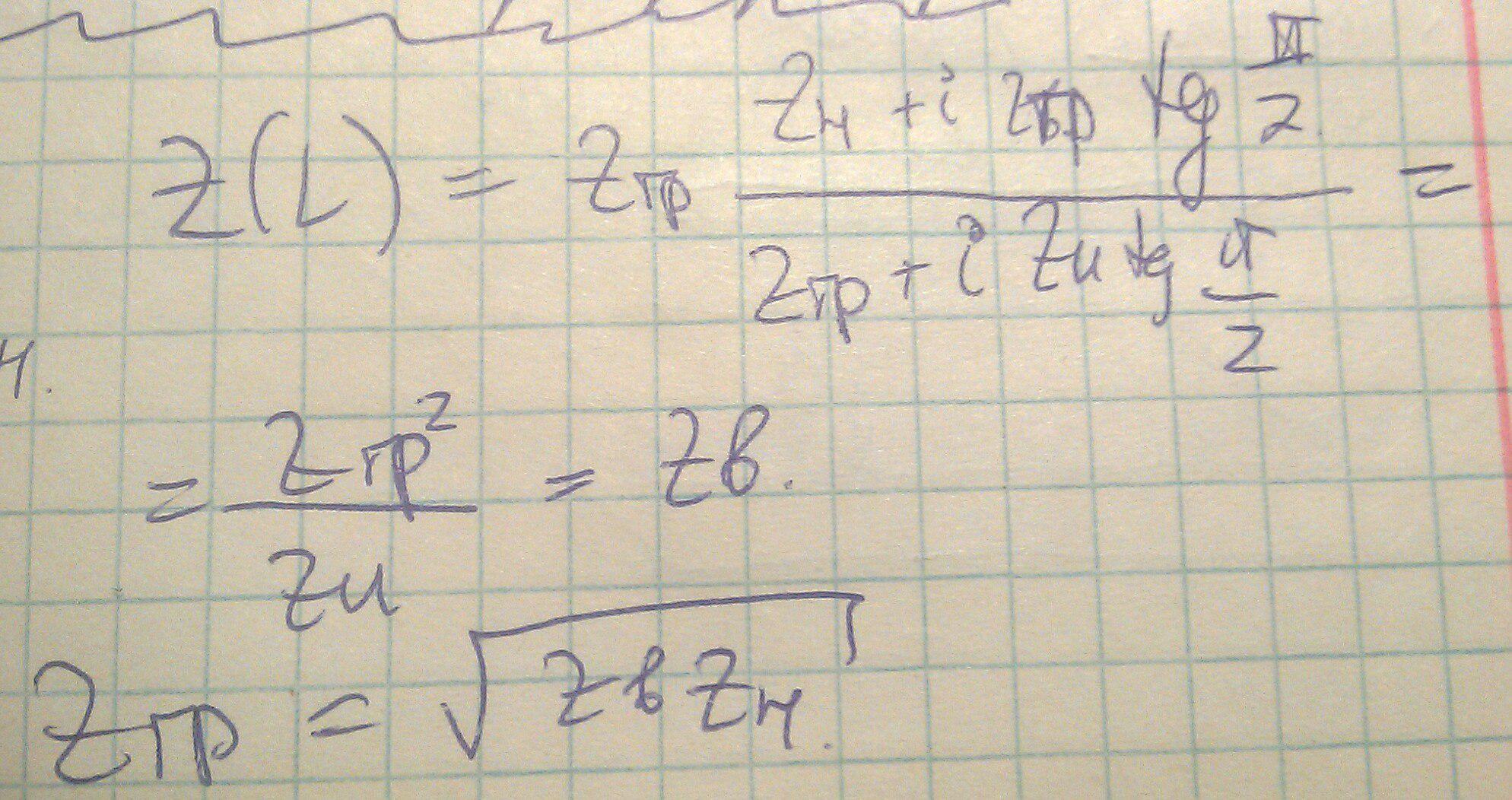
Задача:
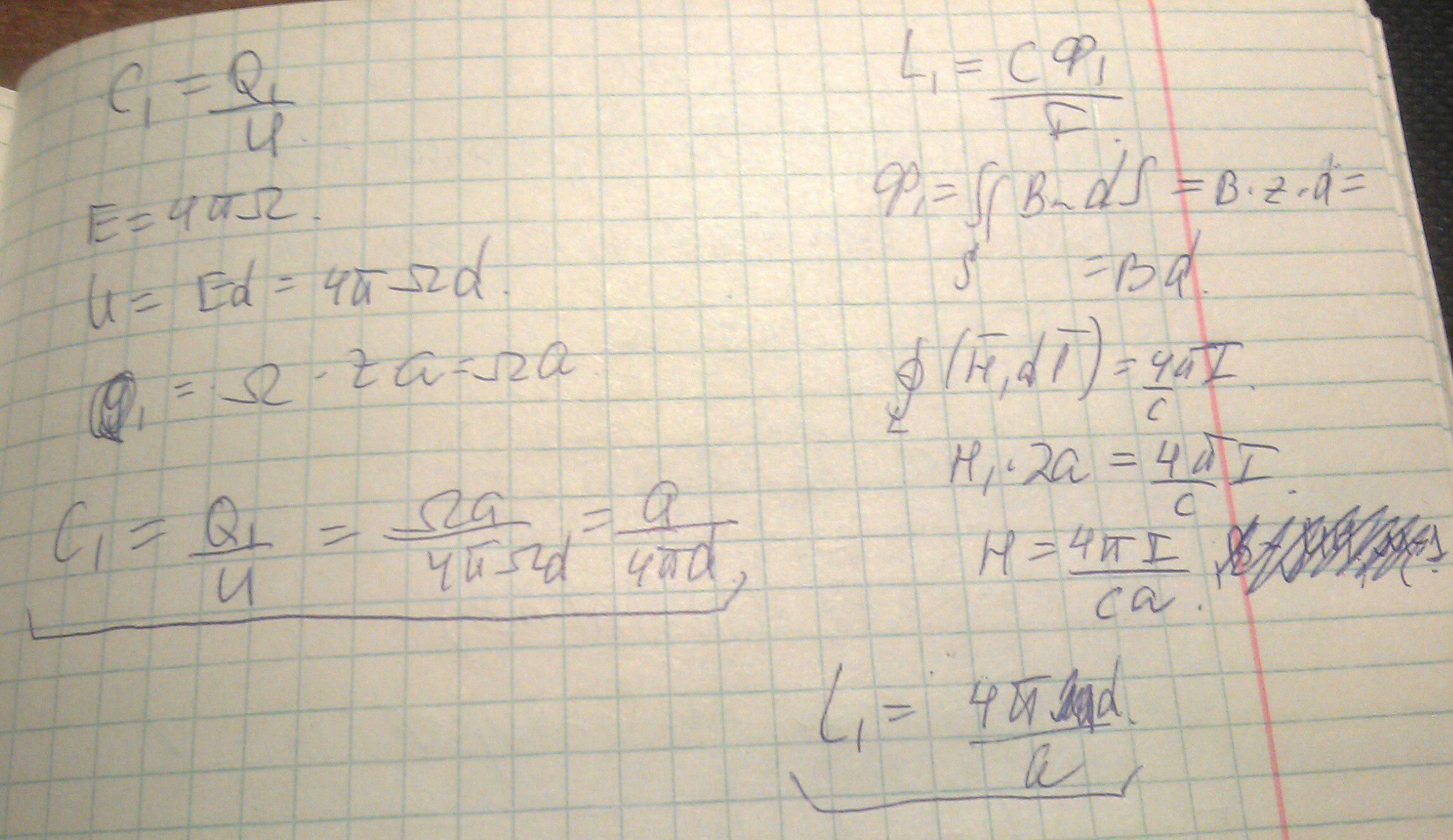
<<Предыдущая лекция Оглавление Следующая лекция>>