Что бы получить резонатор достаточно закоротить волновод с двух торцевых сторон.
Для начала рассмотрим волновод, закороченный с одной стороны.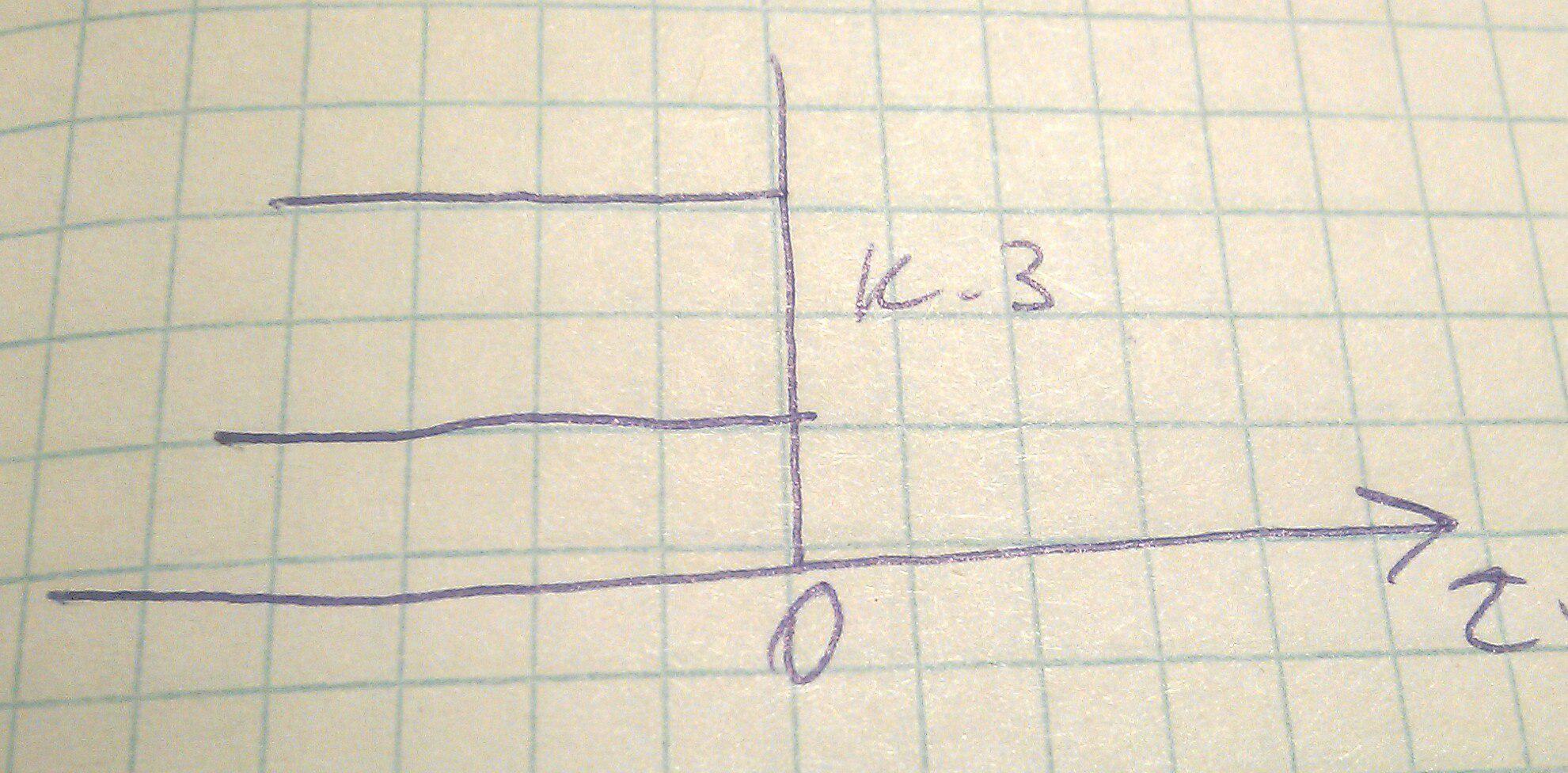
Рассмотрим граничные условия при z=0 и поля внутри данного волновода: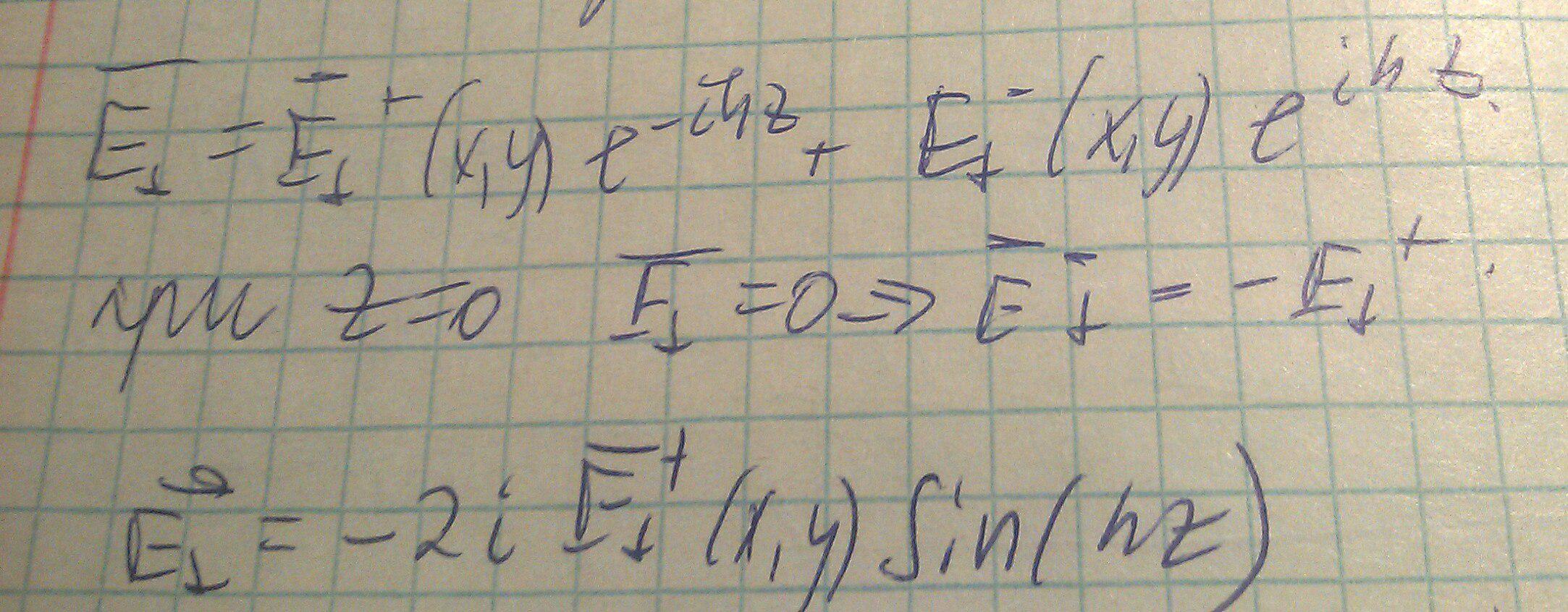
Используем формулы представляющие поперечные компоненты через продольные в двух направлениях: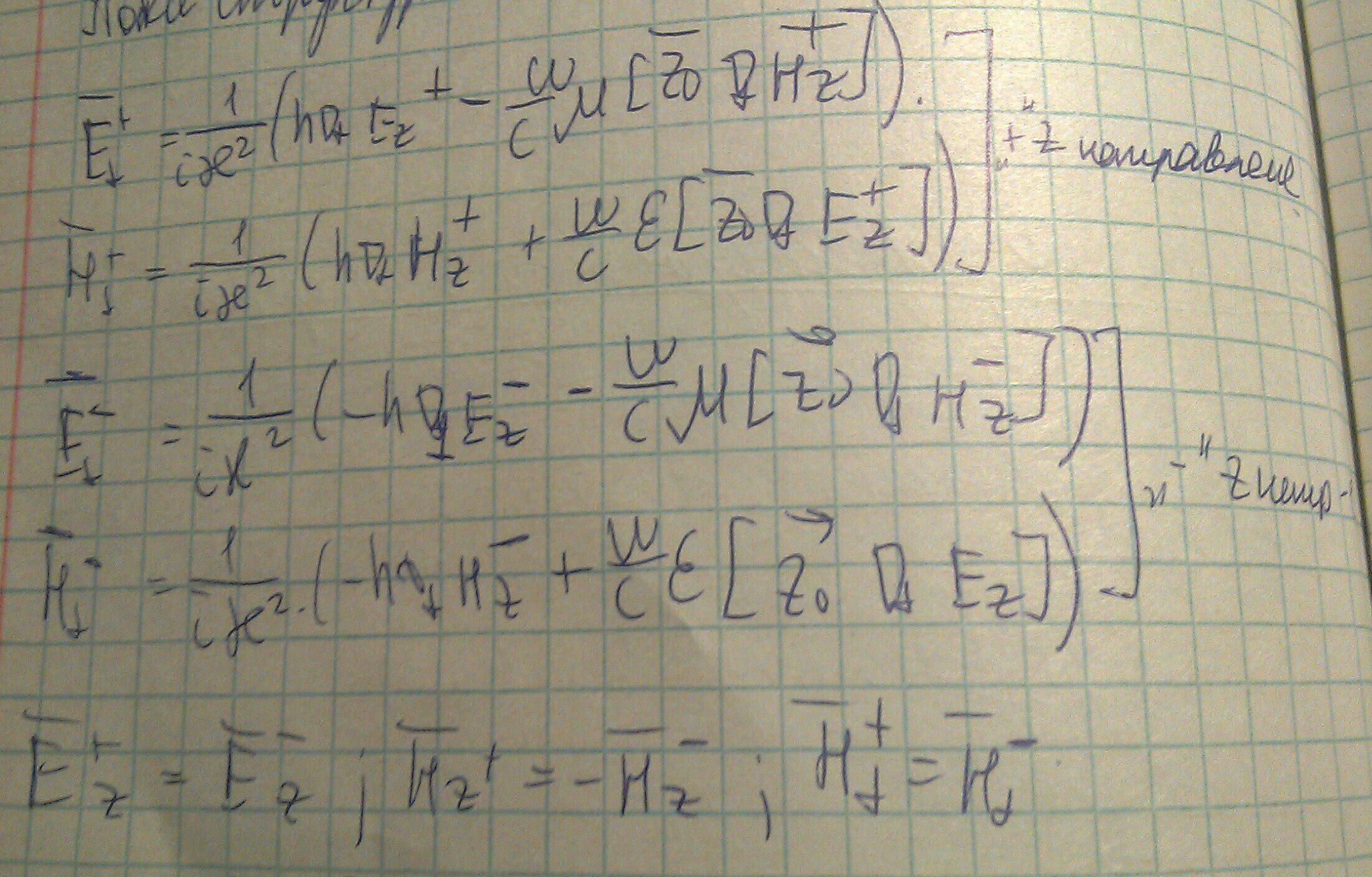
Окончательно получим: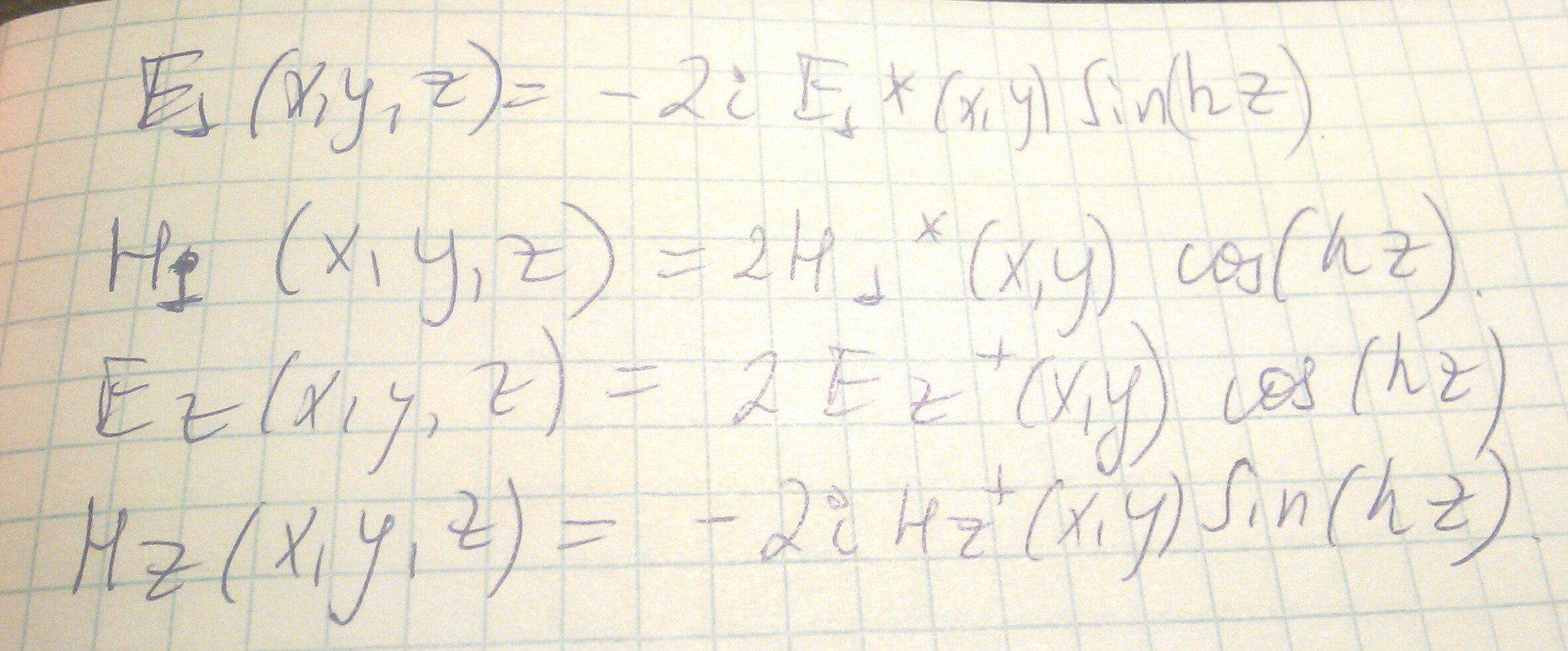
Значит для любого волновода закороченного с одной стороны, зная структуру любой моды бегущей волны, можно получить выражения для полей в резонаторе.
Поставим перегородку из идеального проводника в точках со следующими координатами, что бы получить резонатор: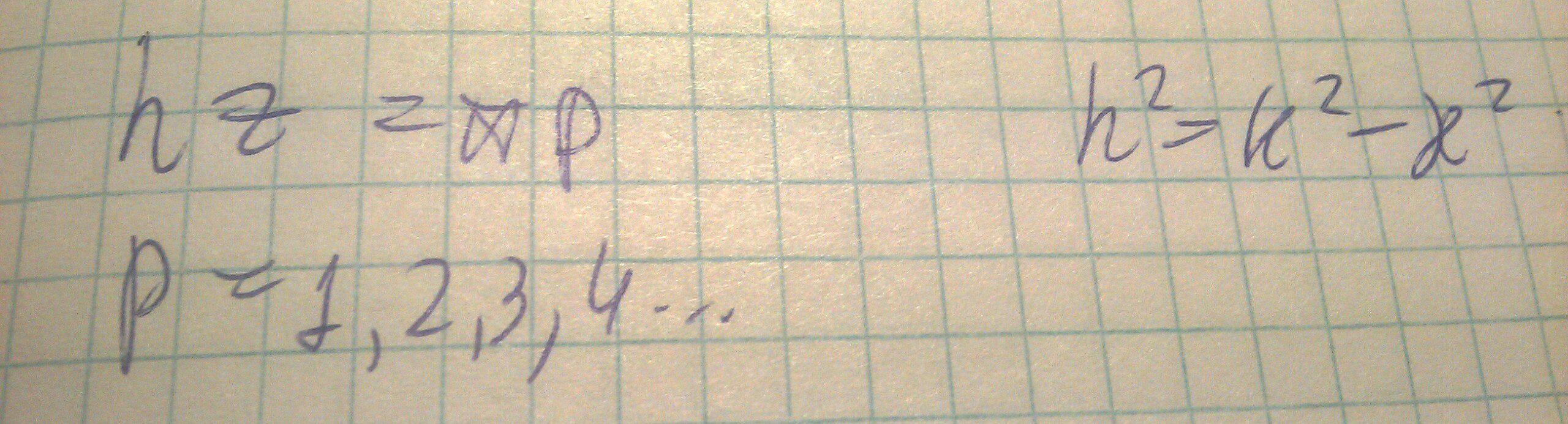
Берем отрезок длины z=L, тогда: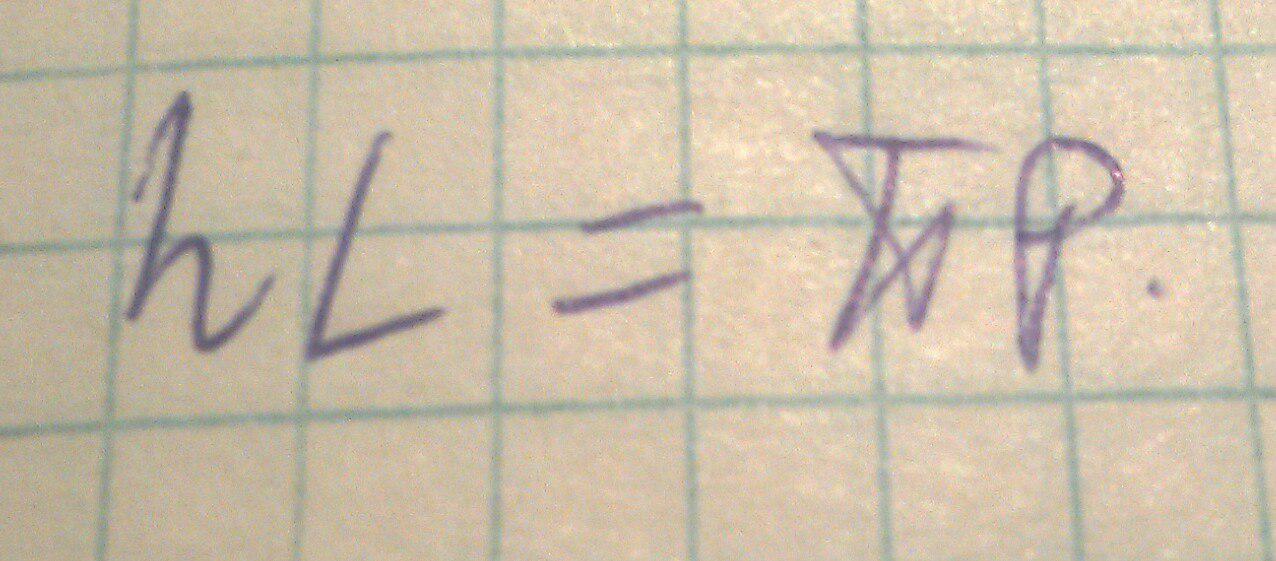
В волноводе, который ограничен с двух сторон, продольное волновое число не произвольное, при этом волновое число: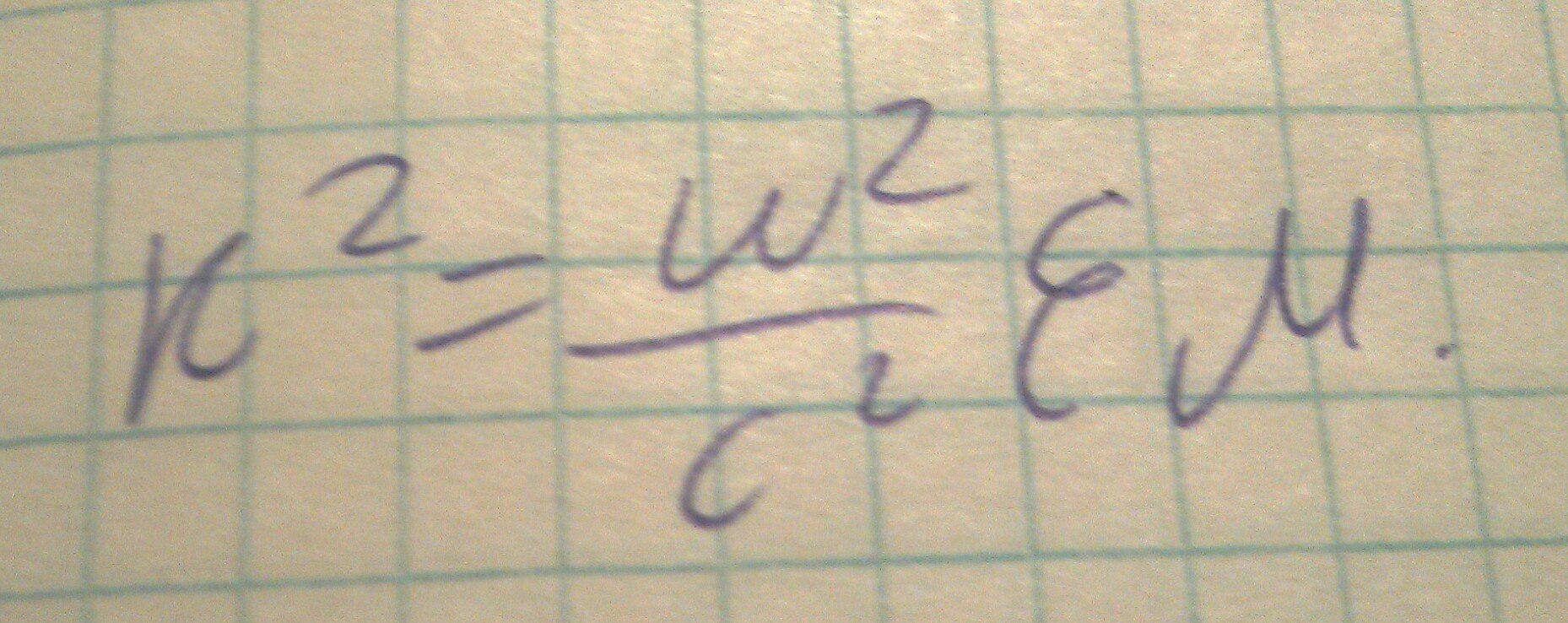
Из данных выражений следует, что в такой системе могут существовать колебания в дикретном наборе частот, которые называются резонансными или собственными.
У колебательного контура одна резонасная частота, а в резонаторе дискретный набор частот, удовлетворяющий условию: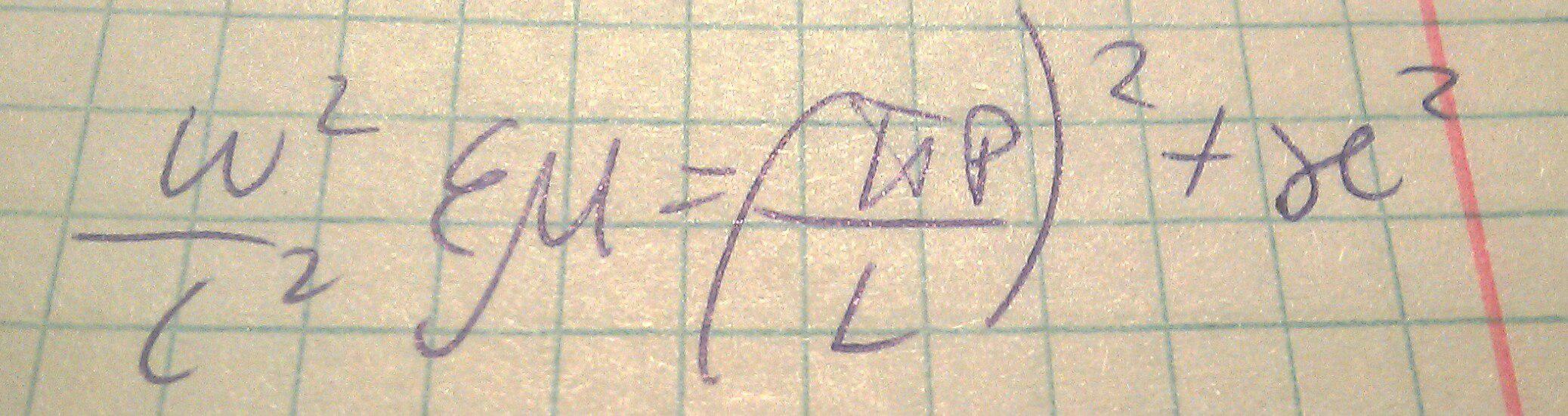
Рассмотрим прямоугольный резонатор с идеально проводящими стенками: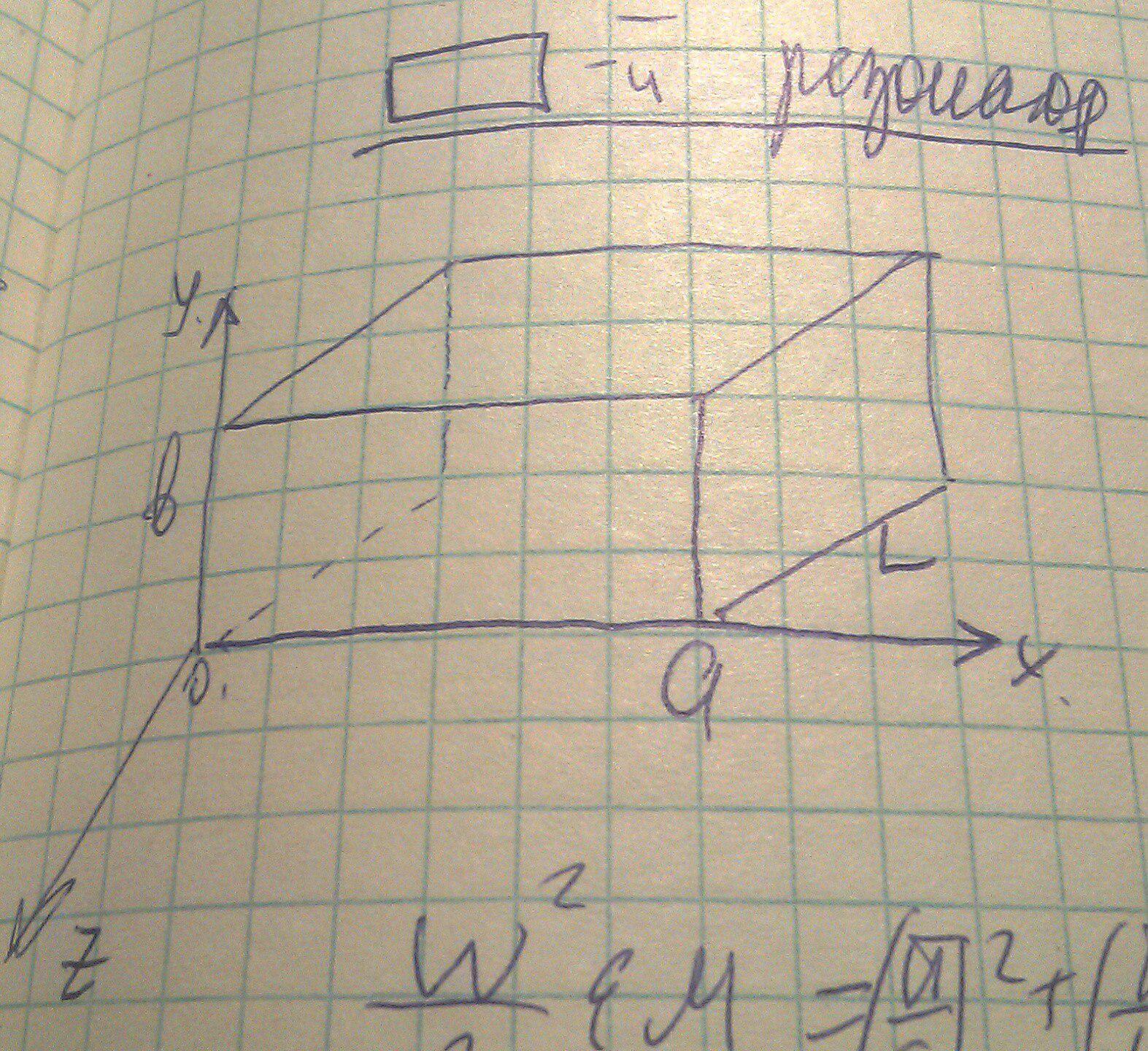
Можно ввести классификацию мод волн волновода ТЕnmp и ТМnmp.
При таком соотношении главная мода данного резонатора, то есть мода имеющая минимальную собственную частоту - TE101, при этом: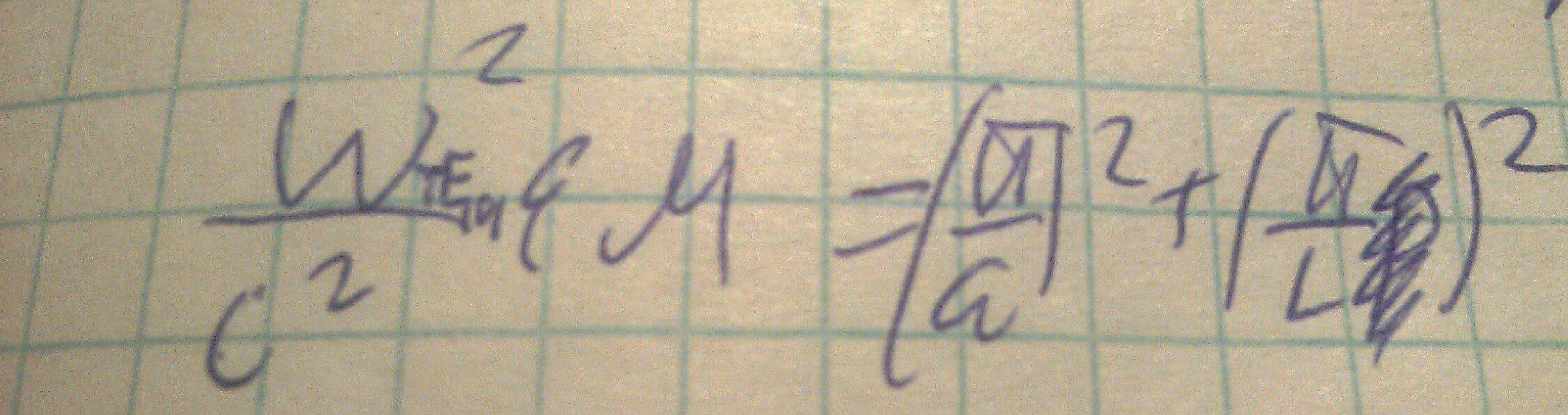
Найдем все поля для данной моды данного резонатора.
Выразим компоненты поля, зная выражение Ey для прямоугольного резонатора моды TE101: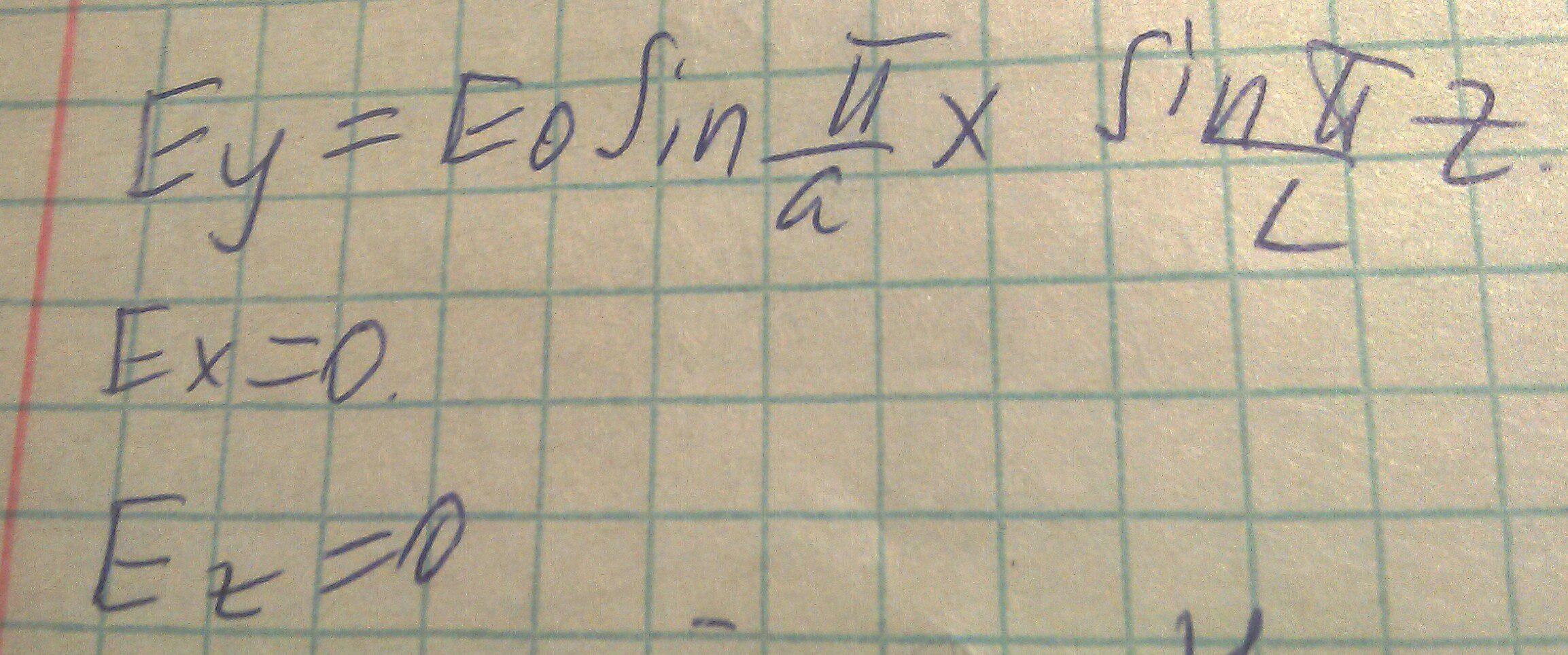
Выразим составляющие магнитного поля: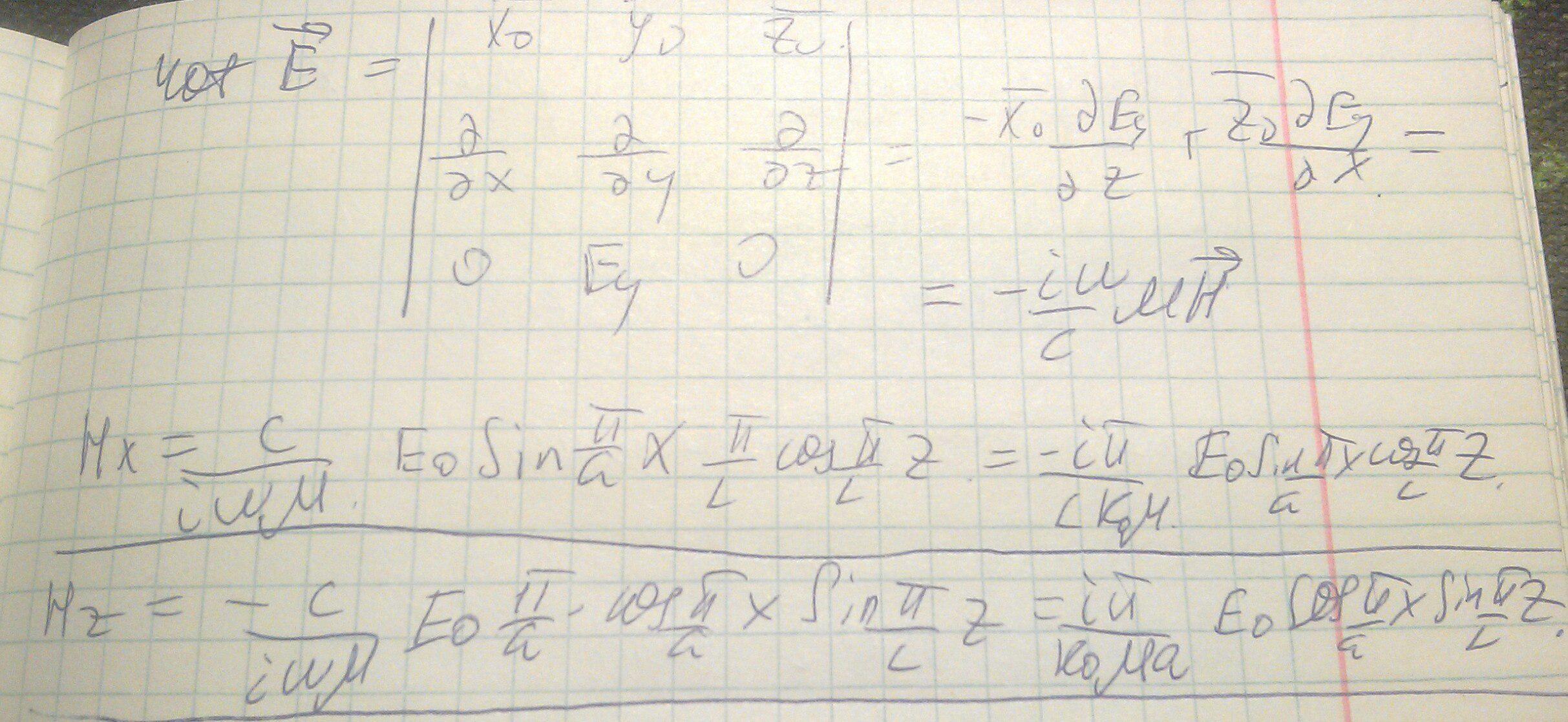
Для того, что бы изобразить картины силовых линий главной моды резонатора, найдем мгновенные значения. Для этого запишем комплексный множитель и возьмем реальную часть от получившегося выражения:
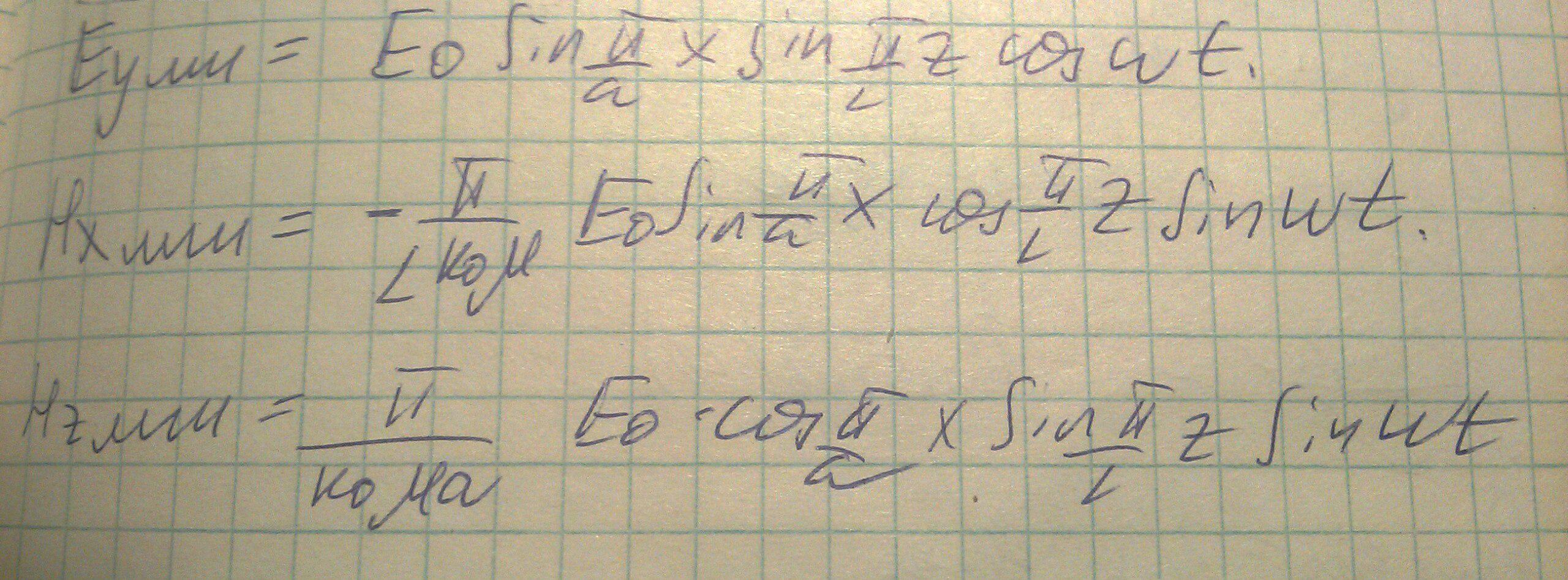Картины силовых линий будут выглядеть следующим образом: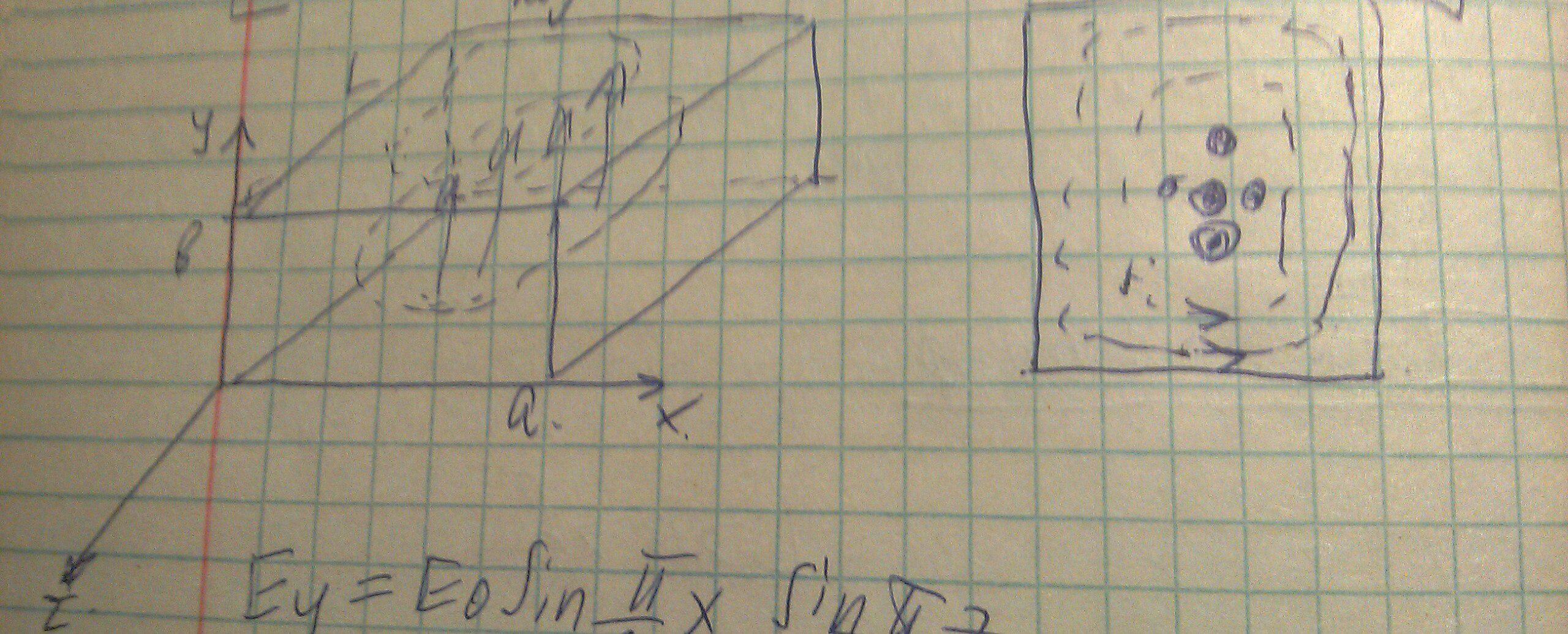
<<Предыдущая лекция Оглавление Следующая лекция>>