Кортикальная криптография

Введение

Криптографические системы как правило полагаются на секретность ключа выдаваемого пользователю. Но однако подавляющая их часть не защищена от атак с использованием человеческого фактора. Такие атаки называются бандитским криптоанализом, и как правило являются самым простым способом борьбы с криптографией. 

В данной работе рассматривается метод защиты от бандитского криптоанализа с применением концепции имплицитного научения.[2][5]


 

Считается, что за имплицитное научение отвечает отдел мозга, называемый базальные ядра (базальные ганглии), которые позволяют получать такие навыки, как например езда на велосипеде, с помощью многократного их повторения. [3][4]

—Знания полученные таким образом не доступны сознательно человеку обладающему ими.

—В данной работе представлены две компьютерные игры использующие концепцию имплицитного научения последовательности для аутентификации.

Хотя такой пароль может быть использован для аунтефикации, пользователь не может каким-либо образом передать его другому человеку.

 

Имплицитное научение последовательности

В основе криптографической системы, рассматриваемой в данной работе лежит задача имплицитного научения последовательности. [5]

Научение последовательности 

Испытуемым предъявляются зрительные стимулы на каждый из которых нужно реагировать определенным образом (нажатием на соответствующую клавишу). В последовательности появления стимулов могут быть определенные закономерности, о которых испытуемый не знает.
Исследования показали, что со временем время реакции испытуемых на стимулы, появляющиеся в закономерной последовательности, уменьшается. [6]

В предшестующиз работах [5][4] была рассмотрена модель, в которой пользователям нужно было перехватывать движущиеся объекты (кружки) падающие по одному из нескольких достуных столбцов с постоянной скоростью пока не достигали нижнего положения, где они исчезали.
Задачей игрока являлось перехватить каждый объект, достигающий нижнего положения нажатием на клавишу, соответствующую столцу, по которому движется объект. Нажатие неправильной клавиши или бездействие засчитывается как некорректный результат. В течении 30-40 минут тренировки участники завершали несколько тысяч итераций теста со скрытой повторяющейся последовательностью положений объекта в 80% всех итераций. Игра подстраивает скорость движения объектов так,что процент перехваченых объектов составляет около 70%. Знание ключевой последовательности оценивается сравнением результативноти на тренированной последовательности и нетренированной.
После участникам прелагали различные фрагменты ключевой последовательности и фрагменты случайной последовательности.  Как оказалось большинство испытуемых не узнавали ключевую последовательность.
 
 

Простейшая система аутентификации использующая имлицитное научение последовательности

Исползование имплицитного научение последовательности даёт возможность создать систему аутентификации. 
Работу системы идентификации опирается на два шага: 

• Тренировка
• Аутентификация

В тренировочной стадии испытуемый выполняет задачу научения последовательности состоящей из символов набора K = {a;b;c;d…}.. В качестве ключевой последовательности использовались только Эйлеровы циклы графа, изображённого на рис.2. Таким образом подпоследовалености из двух символов —такие как {a;b},{c;d},{d;a} и тд.встречаются только один раз.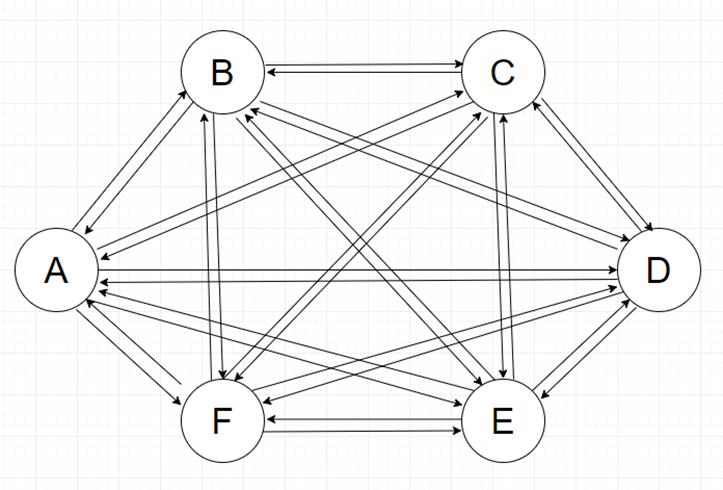 





рис.2 

Число возможных ключевых последовательностей можно рассчитать из теоремы и числе Эйлеровых циклов в графе[7].
например, для набора из 6 символов длина Эйлерова цикла составляет 30 символов, а количество возможных ключевых последовательностей равно 6^4*24^6=2^37.8. Следовательно полученный пароль имеет почти 38 бит энтропии, что гораздо больше чем у стандартных паролей.
Ключевая последовательность внедряется в общую случайную последовательность так, что 

Преимущества перед биометрической аутентификацией

Ключевая последовательность может рассматриваться как биометрический ключ для аутентификации тренированного пользователя.
Однако подобный метод имеет значительные преимущества перед обычной биометрической криптографией.

1) В отличие от биометрии, аутентификационные данные пользователей не могут быть скопированы или раскрыты даже при их желании.

—2) Наличие возможности сменить аутентификационные данные.

Игра 1
Игра 2
Результаты

[1] Н. В. Морошкина, В. А. Гершкович. Актуальные тенденции в исследовании имплицитного научения, 2014.

[2] A. Destrebecqz and A. Cleeremans. Can sequence learning be implicit? new evidence with the process dissociation procedure. Psychonomic Bulletin& Review, 8:343–350, 2001.

[3] Matthew D. Lieberman. Intuition: A Social Cognitive Neuroscience Approach c.113

[4] Hristo Bojinov, Daniel Sanchez, Paul Reber, Dan Boneh, Patrick Lincoln. Neuroscience Meets Cryptography: Designing Crypto Primitives Secure Against Rubber Hose Attacks

[5] D. Sanchez, E. Gobel, and P. Reber. Performing the unexplainable: Implicit task performance reveals individually reliable sequence learning without explicit knowledge. Psychonomic Bulletin & Review, 17:790–796, 2010.

[6] A. Cleeremans, A. Destrebecqz, M. Boyer. Implicit learning: news from the front // Trends in Cognitive Sciences. — 1998-10-01. — Т. 2, вып. 10. — С. 406–416.

[7] J. Benaloh and D. Tuinstra. Uncoercible communication. Technical Report TR-MCS-94-1, larkson University, 1994.

[8] Ran Canetti, Cynthia Dwork, Moni Naor, and Rafail Ostrovsky. Deniable encryption. In CRYPTO,  стр. 90–104, 1997.

[9] Scott Barry Kaufman , Colin G. DeYoung , Jeremy R. Gray, Luis Jiménez, Jamie Brown, Nicholas Mackintosh. Implicit learning as an ability. Cognition 116 (2010) 321–340

[10] Jennifer C. ROMANO BERGSTROM, JAMES H. HOWARD and DARLENE V. HOWARD Enhanced Implicit Sequence Learning in College-age Video Game Players and Musicians Applied Cognitive Psychology, Appl. Cognit. Psychol. (2011) Published online in Wiley Online Library (wileyonlinelibrary.com) DOI: 10.1002/acp.1800

[11] Когнитивная психология: история и современность. Хрестоматия. / Под ред. М. Фаликман и В. Спиридонова. М., 2011. С. 156-166.

[12] Chris Soghoian. Turkish police may have beaten encryption key out of TJ Maxx suspect, 2008. cnet.com/news/turkish-police-may-have-beaten-encryption-key-out-of-tj-maxx-suspect/

[13] Paul Reber. Cognitive neuroscience of declarative and non-declarative memory. Parallels in Learning and Memory, Eds. M.Guadagnoli, M.S. deBelle, B. Etnyre, T. Polk, A. Benjamin, pages 113–123, 2008.

[14] Морошкина Н.В. Влияние конфликта имплицитных и эксплицитных знаний субъекта на результаты научения в задаче классификации  // Экспериментальная психология. 2013. Том 6. № 3. С. 62–73.

[15] Mary J. Nissen and Peter Bullemer. Attentional requirements of learning: Evidence from performance measures. Cognitive Psychology, 19(1):1–32, January 1987.

[16] Julien Doyon, Pierre Bellec, Rhonda Amsel,Virginia Penhune, Oury Monchi, Julie Carrier, St´ephane Leh´ericy, and Habib Benali. Contributions of the basal ganglia and functionally related brain structures to motor learning. Behavioural Brain Research, 199(1):61–75, April 2009.

[17] D.J. Sanchez and P.J. Reber. Operating characteristics of the implicit learning system during serial interception sequence learning. Journal of Experimental Psychology: Human Perception and Performance, in press.

[18] Circuits and trees in oriented linear graphs. Simon Stevin, 28:203–217, 1951.

[19] Graham R. Brightwell, Peter Winkler. Note on Counting Eulerian Circuits. May 2004 CDAM Research Report LSE-CDAM-2004-12

[20] Аксель Клерманс, Арно Дестребекс, Мод Бойер. Имплицитное научение. 2011

[21] Wikipedia. Бандитский криптоанализ.