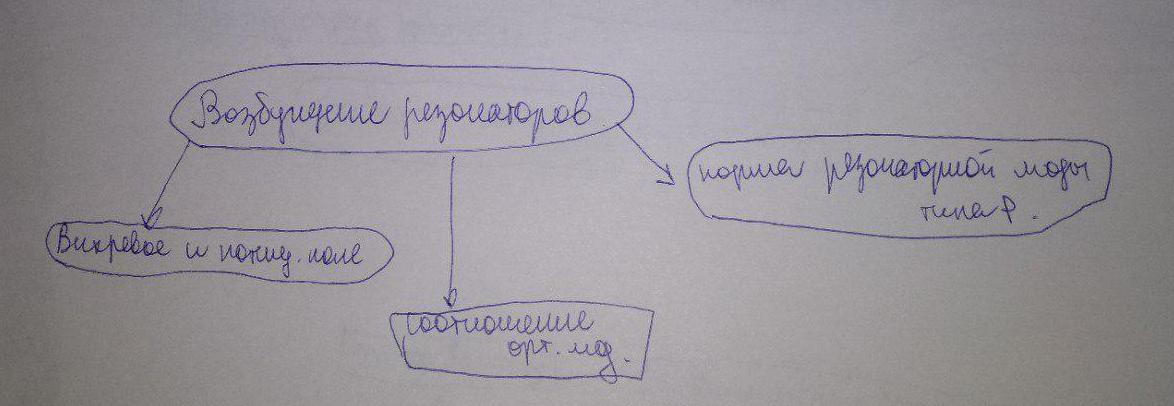


Запишем поле через вихревую и потенциальную компоненты: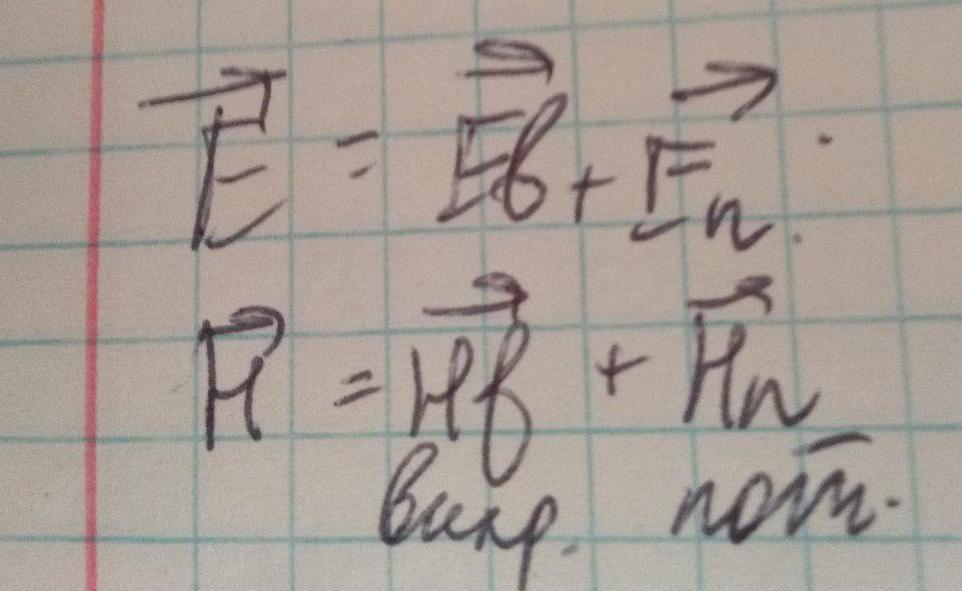
Интерес прежде всего представляет вихревое поле: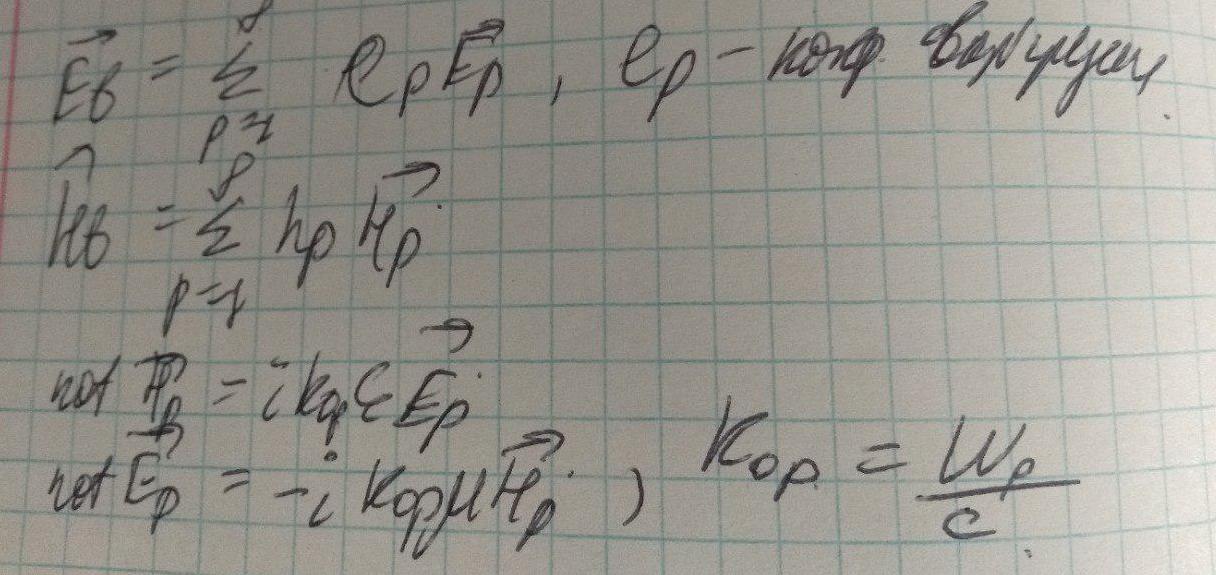
Докажем соотношение ортогональности мод: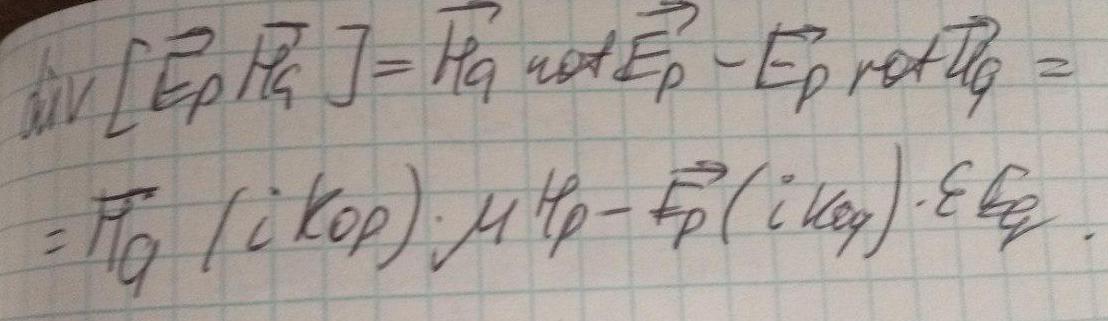
Проинтегрируем по обьёму резонатора: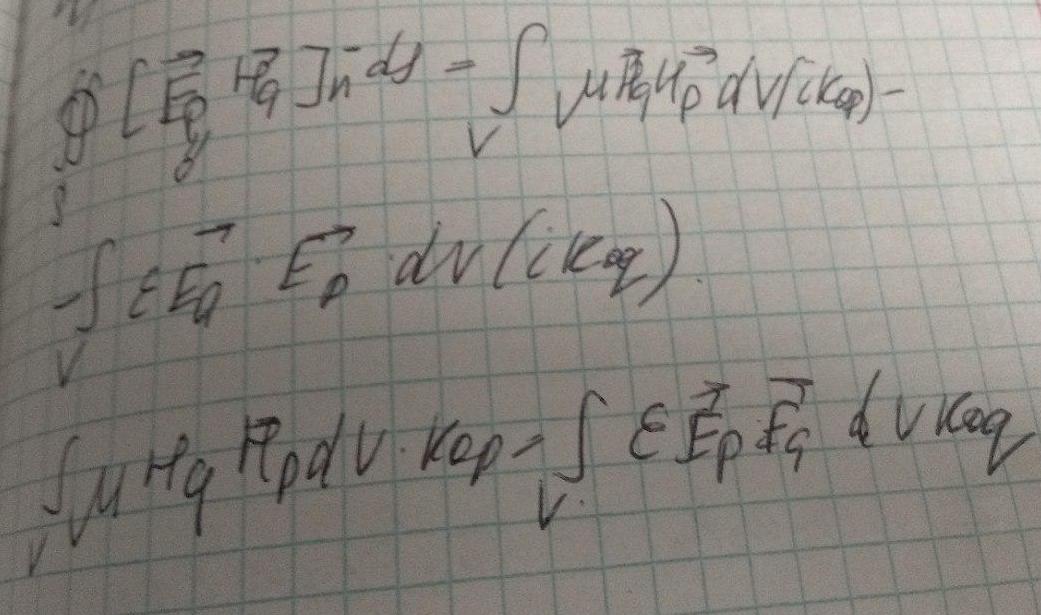
Делаем смену обозначений q на p и наоборот: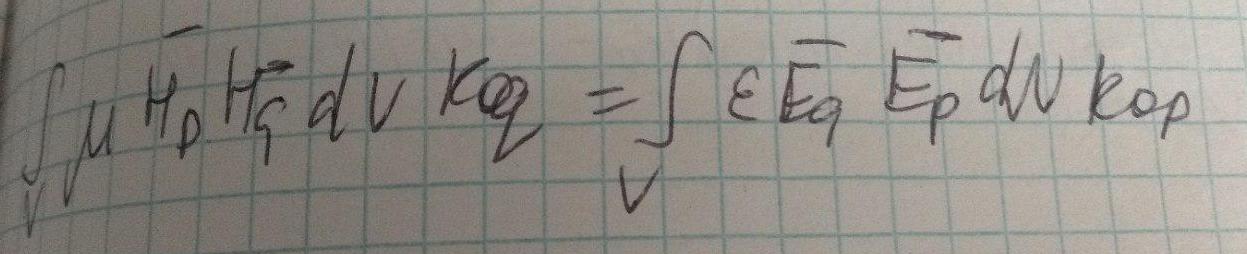
Рассматриваем как систему уравнений. Решаем при Kop²=Koq², если не так то интеграл равен 0.
Отсюда следует соотношение ортогональности: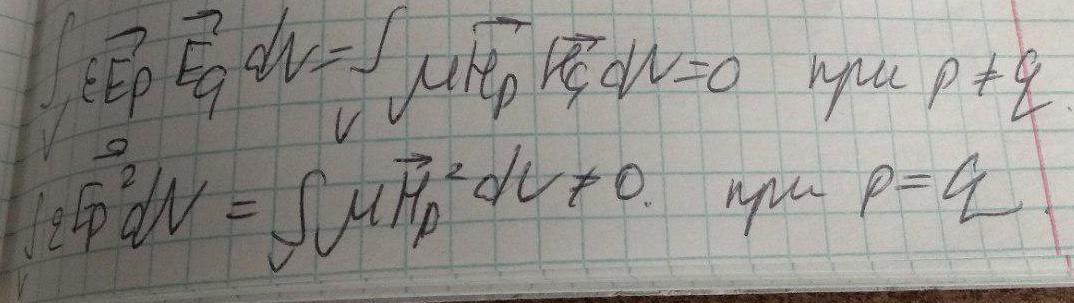
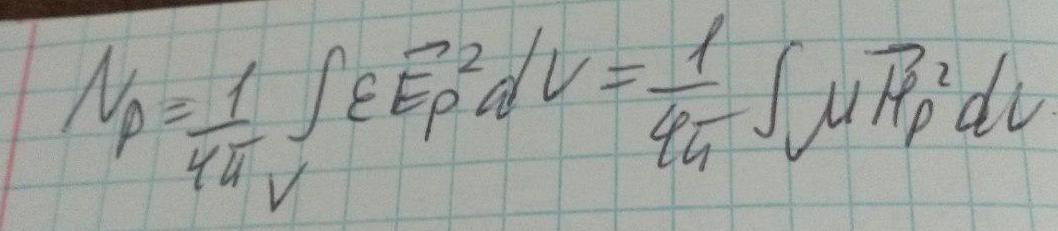
Запишем уравнения Максвелла для искомых полей, подставим одну систему в другую и получим*: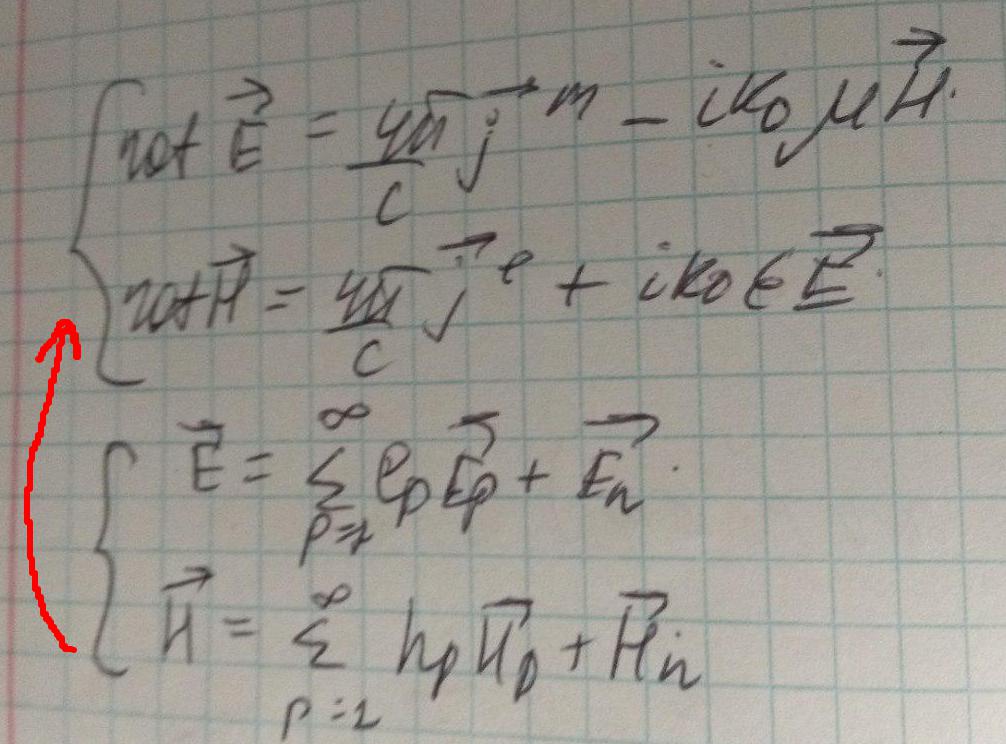
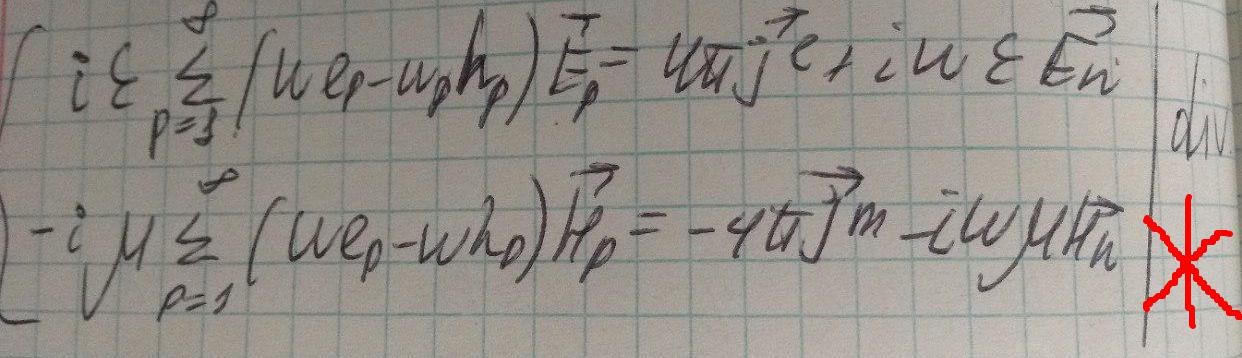
Очевидно что div от вихревых полей = 0. Из этого условия и уравнений непрерывности получим: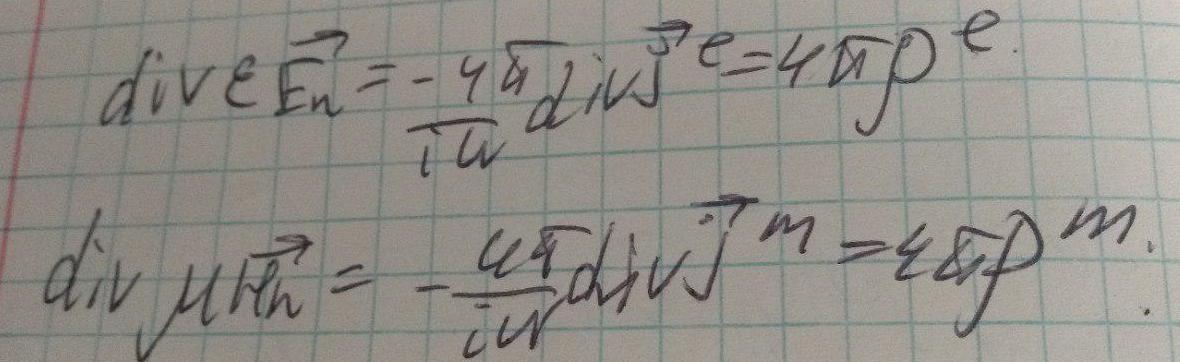
Потенциальные поля описываются уравнениями статики: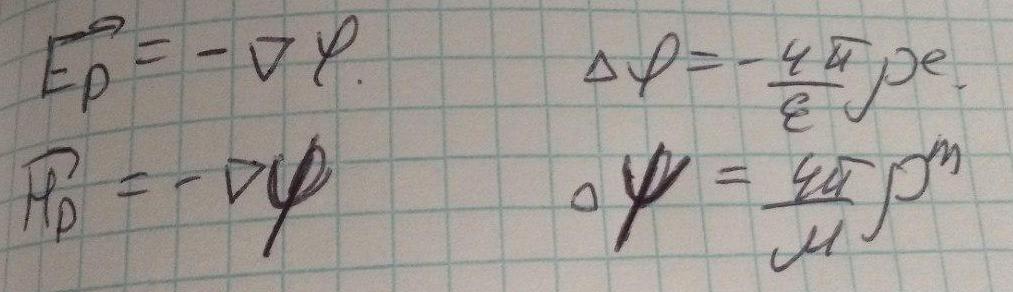
Если первое выражение в * умножить на Ep, а второе на Hq, воспользовавшись свойством ортогональности мод, можно показать что интеграл по Ep обращается в 0, тогда по св-ву ортогональности получаем следующие выражения: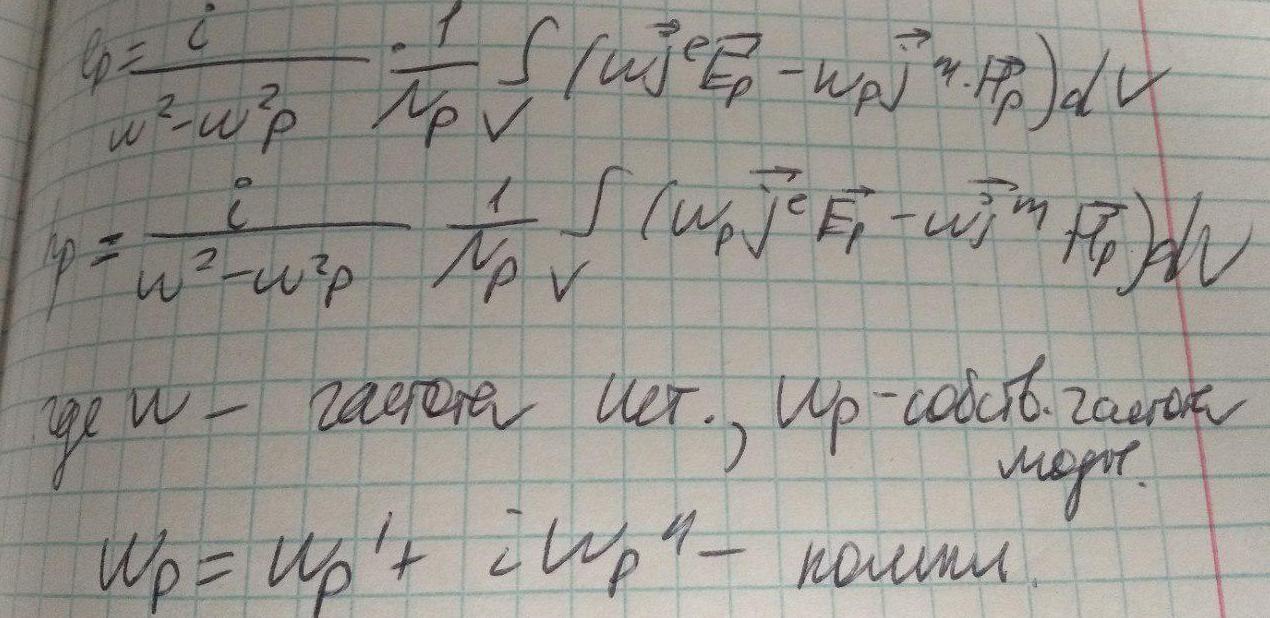
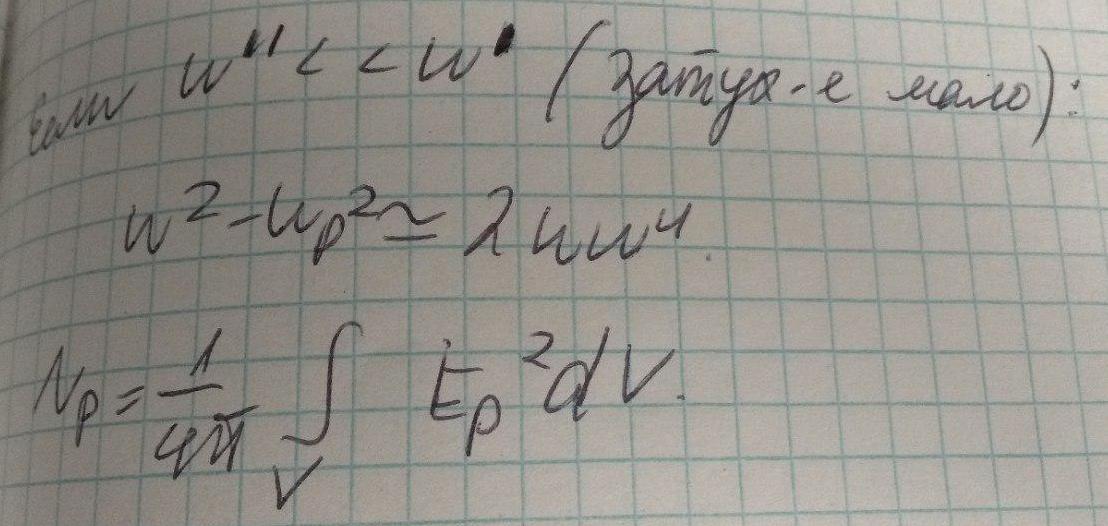
<<Предыдущая лекция Оглавление Практика>>