Оглавление

Телеграфне уравнения

Телеграфные уравнения — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи. 

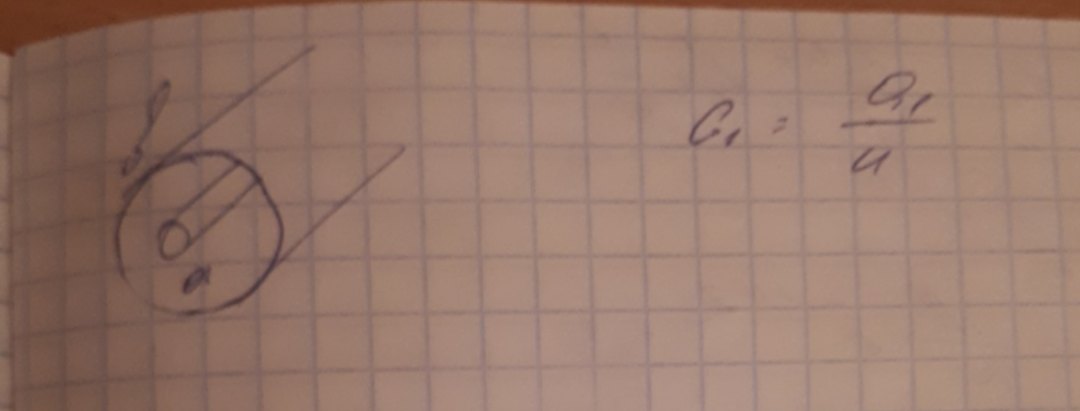
 Будем решать задачу на нахождение телеграфных уравнений на основе коаксиального волновода.

Найдём вспомогательные соотношения: погонную ёмкость-C1 и погонную индуктивность-L1 коаксиальной линии.

Решаем статическую задачу нахождения разности потенциалов между 2-мя коаксиалами на заряд. Теорема Гаусса: 

Чтобы воспользоваться этой теоремой, нужно "посадить" заряды на проводник. Делаем предположение о структуре поля" исходя из симметрии задачи, структура поля имеет вид: 

Найдем  L1

Запишем уравнение непрерывности (в комплексной форме) и проинтегрируем его для коаксиала:

Вопсользуемся уравнением Максвелла в интегральной форме:

Получим уравнение для I и U в ТЕМ волнах, используя 1-е и 2-е Телеграфные уравнения:

Получим уравнение для напряженности (подставим ток из 1-го уравнения во 2-е):

Волновое сопротивление-отношение амплитуды напряжения к амплитуде тока в бегущей волне:

Формула пересчёта импедансов

Введем импеданс в сечении линии:

Слева от нагрузки волны представляют собой сумму волн, бегущих от нагрузки к нагрузке

Таким образом, получили искомую формулу

Тест