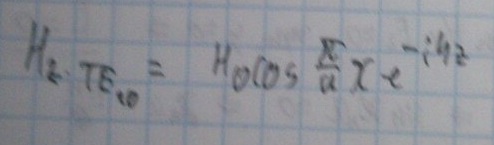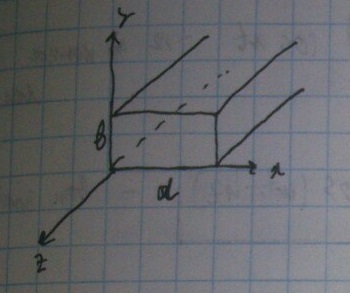
Для нахождения параметров прямоугольного волновода нужно отметить несколько моментов:
Прямогольный волновод представляет из себя волновод с прямоугольным сечением

Запишем краевые задачи для полей данного волновода:

Теперь рассмотрим краевые задачи:

Для решения воспользуемся методом разделения переменных:

Таким образом мы получили выражение для квадрата поперечного волнового числа
Теперь запишем выражение для комплексной амплитуды Еz
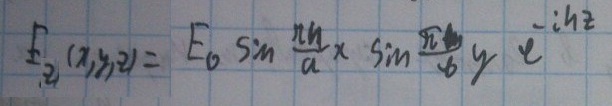
Чтобы перейти к реальным полям, нужно перейти от к комплексных амплитуд к мгновенным значениям
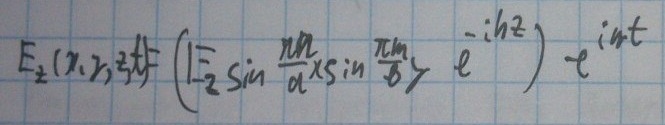
Осталось только взять реальную часть от этого выражения. Тогда получаем:
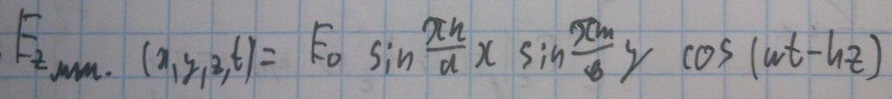
Применив аналогичный подход, получаем:
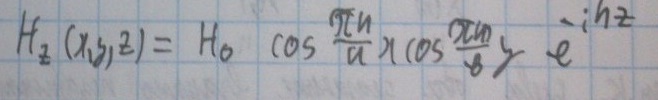
Наименьшее значение поперечного волнового числа соответствует волне H10 (индексы указывают значения n, m) и равно a.
Мода, имеющая минимальную критическую частоту - ТЕ10
Это низшая мода прямоугольного волновода. Если используется волновод на частоте между первой и второй критической, то там может распределятся только одна мода. Это удобно, так как структура поля становится предсказуемой.