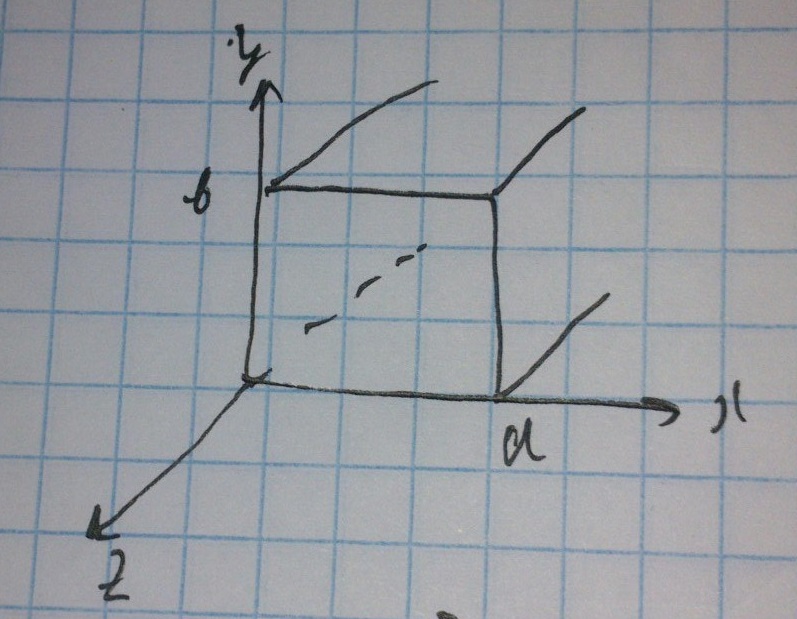
Построим структуру поля H для моды TM11.
Рассмотрим прямоугольный волновод.
Запишем компоненты электрического и магнитного полей:
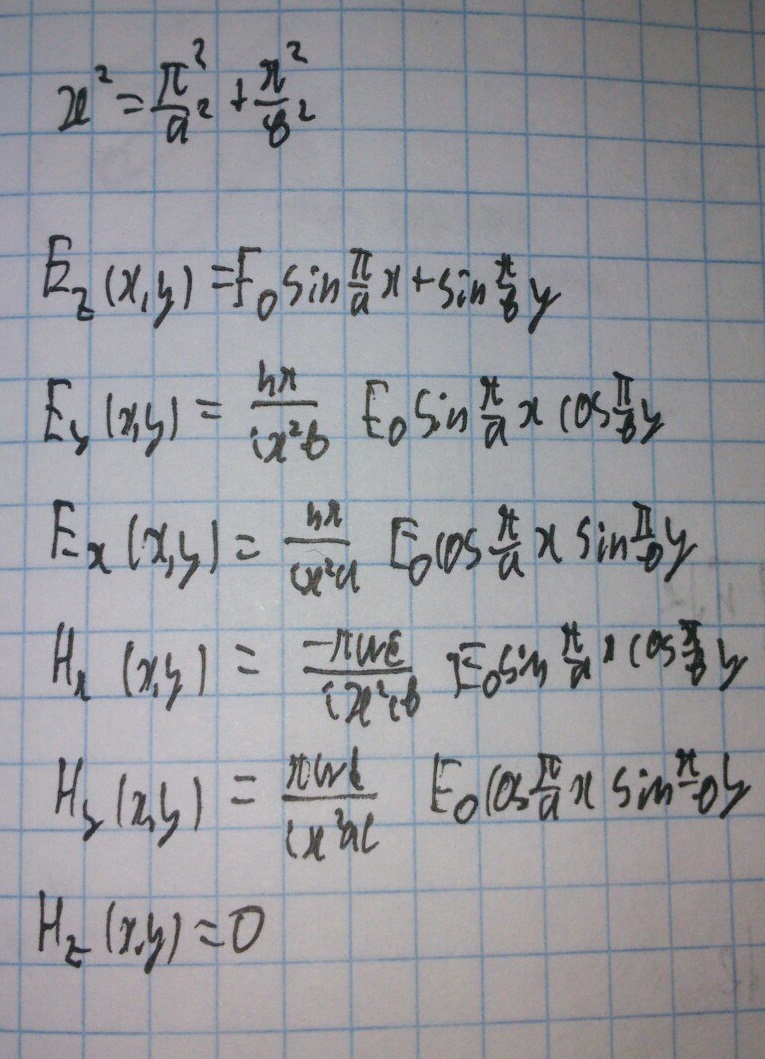
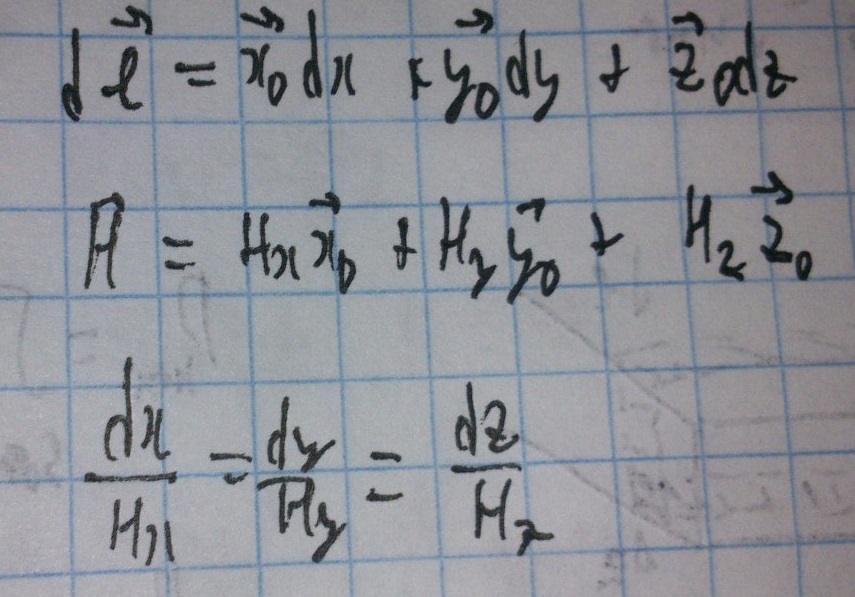
Прейдем к криволинейной системе координат. Для этого добавим коэффициенты Ламе.
Т.к. мы получаем решение уравнения в неявном виде. рассмотрим предельные случаи (при α и β).
Если α и β - малы, то получаем уравнение эллипса (последнее уравнение)
Построим силовые линии в поперечном сечении:
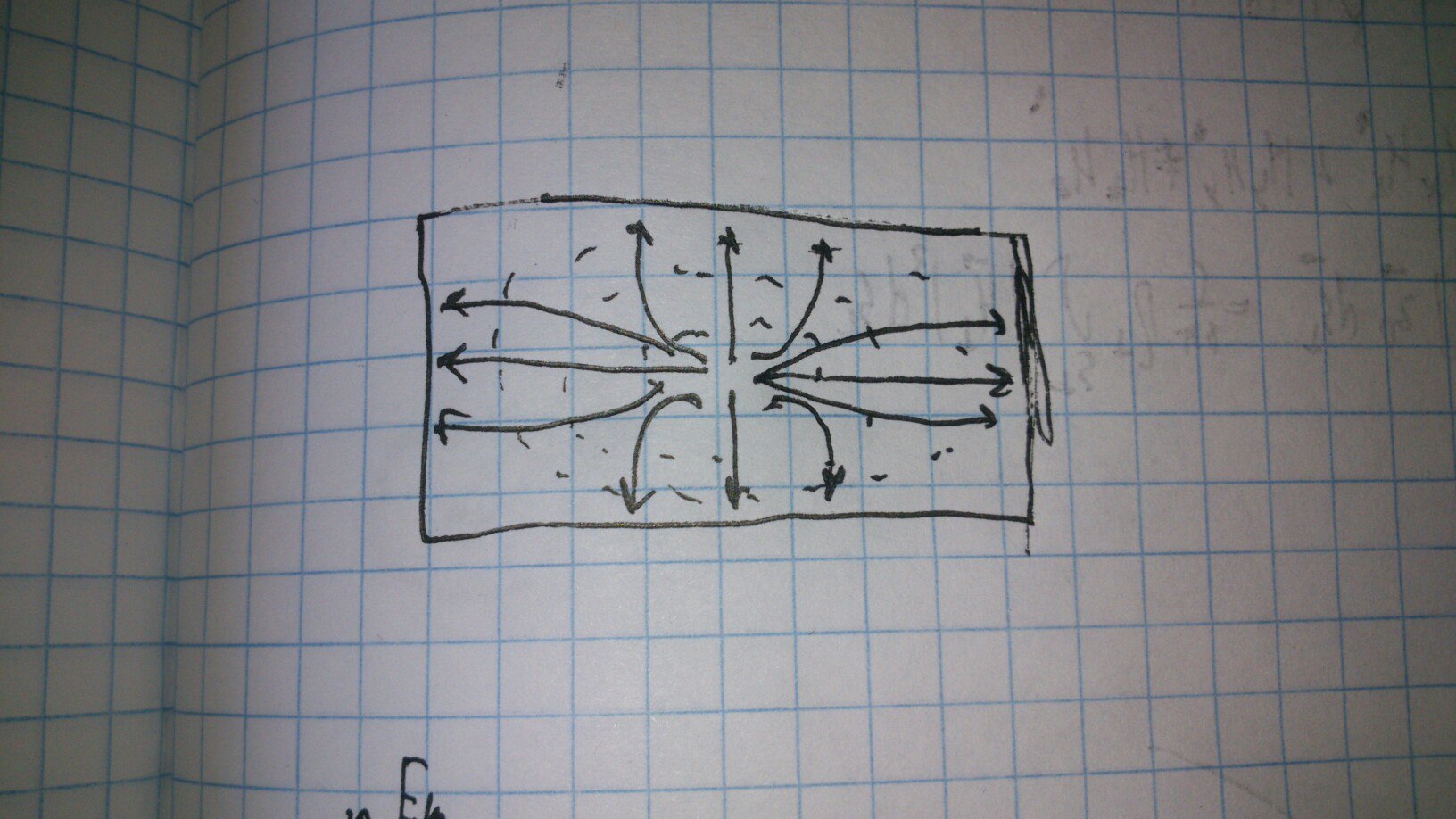
Здесь, как и в прошлой лекции, сплошной линией обозначено электрическое поле, пунктирной - магнитное.
Рассмотрим случай, когда в волноводе используется источник с потерями.
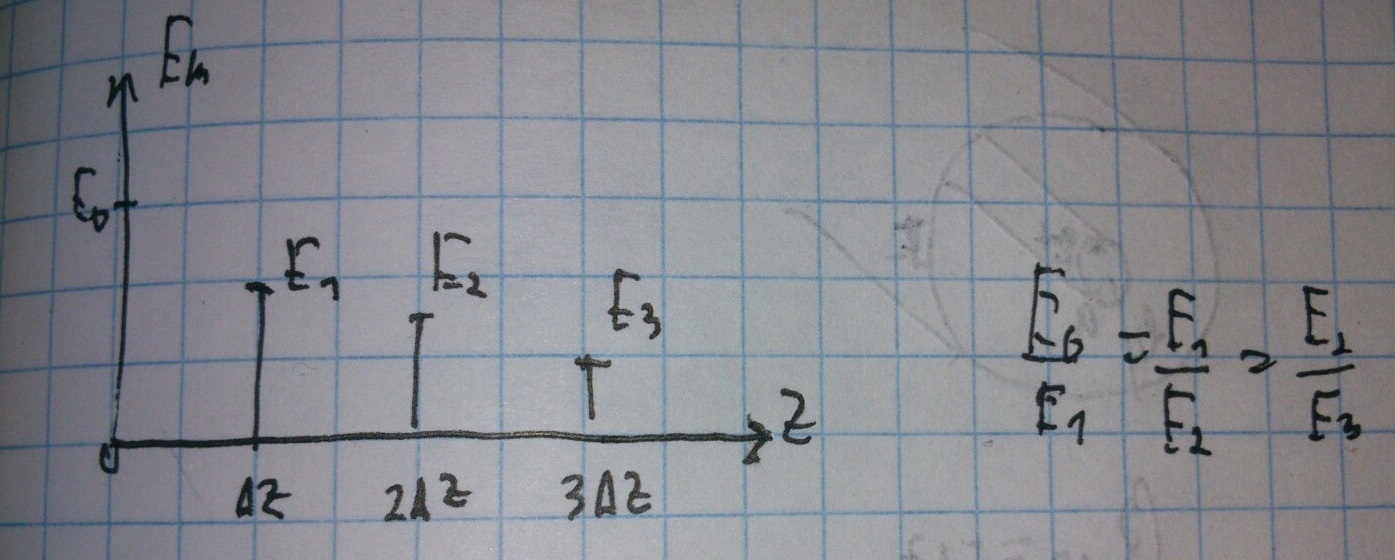
Предположим, что волновод линейный, потери не зависят от уровня поля.
Потери описываются экспоненциальной функцией.
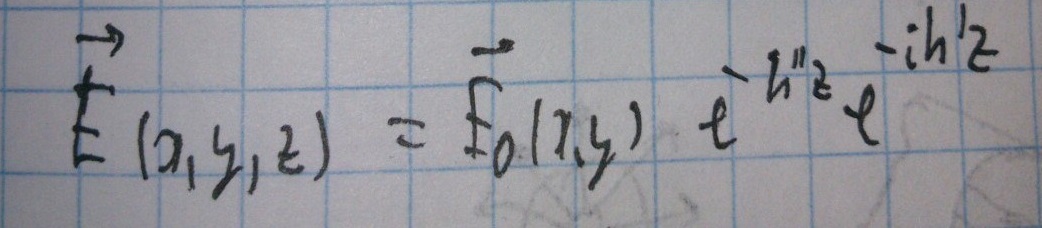
В таком случае к волновому числу добавляется мнимая часть.
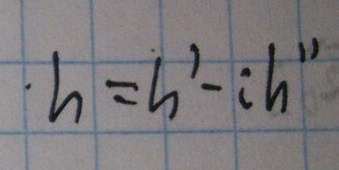, где h — волновое число для идеально проводящих стенок.
h" отвечает за потери. Эту мнимую часть волнового числа называют постоянной затухания.
Знак минус здесь обусловлен тем, что происходит спад при увеличении z.
Для нахождения h'' применим энергетический метод
Вычислим декремент затухания, связав его с переносимой и потерянной мощностью:
Будем считать, что потери в волноводе маленькие и структура полей мод в волноводе с потерями такая же, как в волноводе без потерь (в нулевом приближении).
P считаем таким же, как в волноводе без потерь.
Будем находить P, используя сведения о структуре поля в волноводе без потерь, значении тангенциальной компоненте магнитного поля на стенке.
Воспользуемся граничным условием Леонтовича: 
Оно позволяет найти тангенциальную компоненту магнитного поля через тангенциальную компоненту электрического (на границе с "хорошим" проводником)
Рассмотрим задачу:
Рассчитать постоянную затухания волны моды TE10 в прямоугольном волноводе с поперечными размерами a*b:
a) Если одна из широких стенок не идеально проводящая;
б) Если одна из узких стенок не идеально проводящая
а)
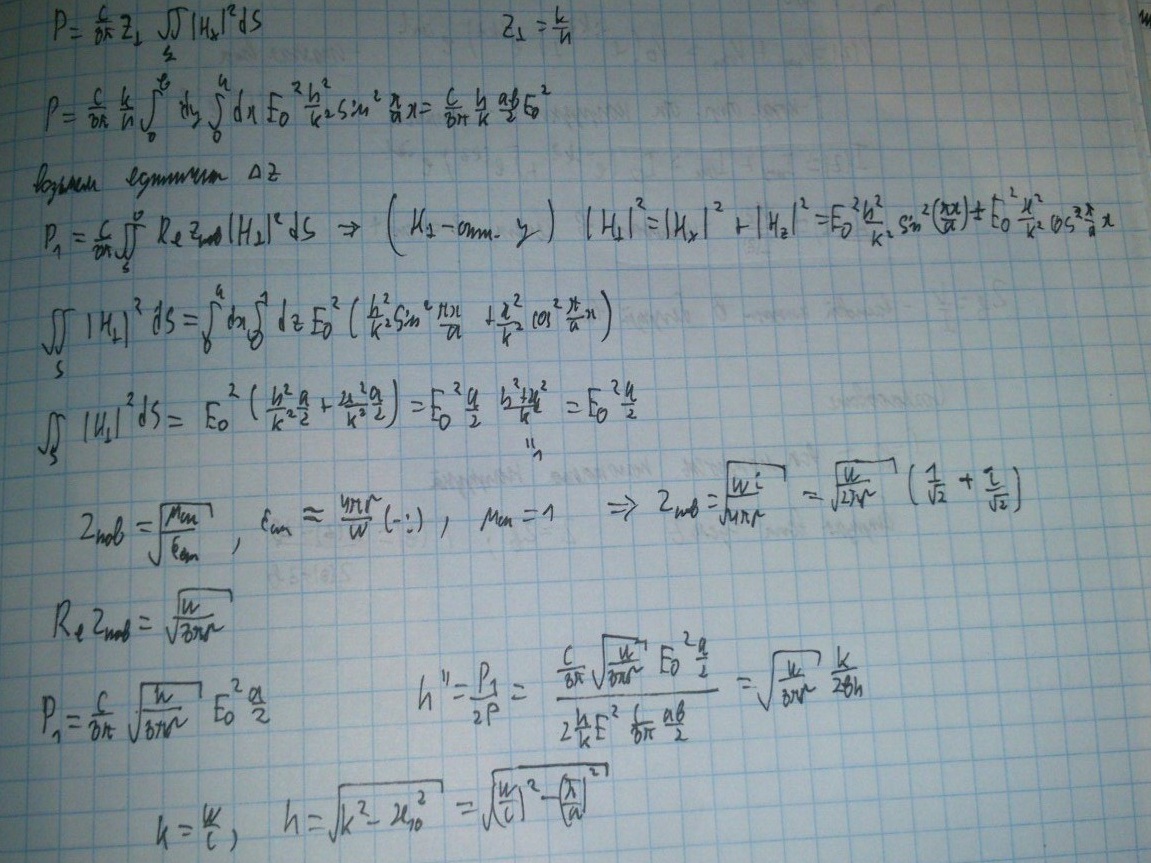
б)
