(к оглавлению)

TEM-волны

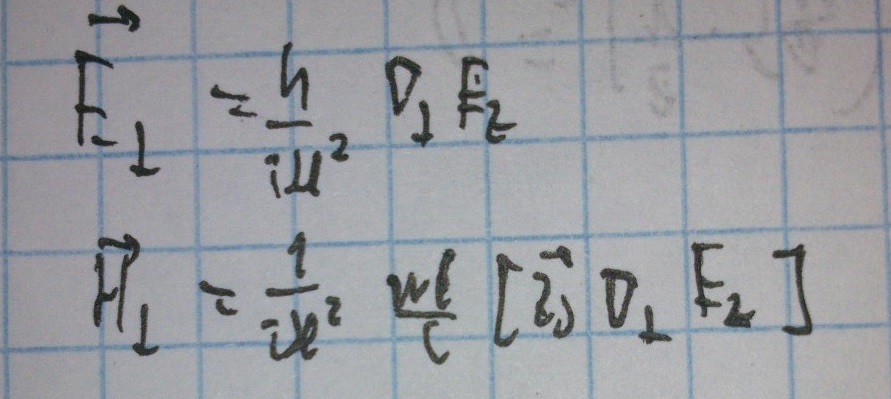
TEM-волны — волны, у которых компоненты электрического и магнитного полей перпендикулярны направлению распространения.

Примером является плоская однородная волна в свободном пространстве.

Рассмотрим предельный случай ТМ волны (z->0):

Напишем формулы поперечных компонент через продольные.

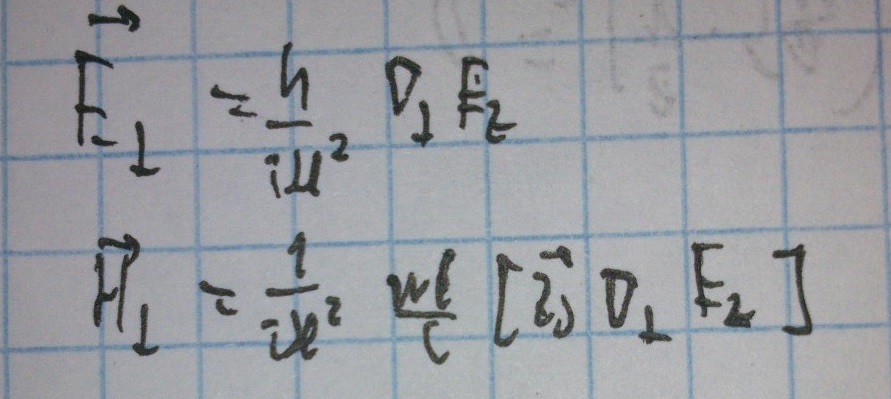
Есть шанс, что мы получим  поперечные компоненты, не равные 0, если квадрат собственного числа равен 0

(получим неопределённость 0/0).

Рассмотрим дисперсионное уравнение в таком случае:

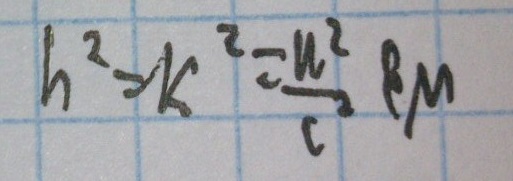
Значит, если такие волны существуют, то это будут волны без дисперсии, т.е. фазовая и групповая скорости будут такими же, как свободном пространстве (т.е. спектр на выходе будет таким же, как и на входе).

Сделаем замену переменных и воспользуемся уравнением Максвелла (без источника):

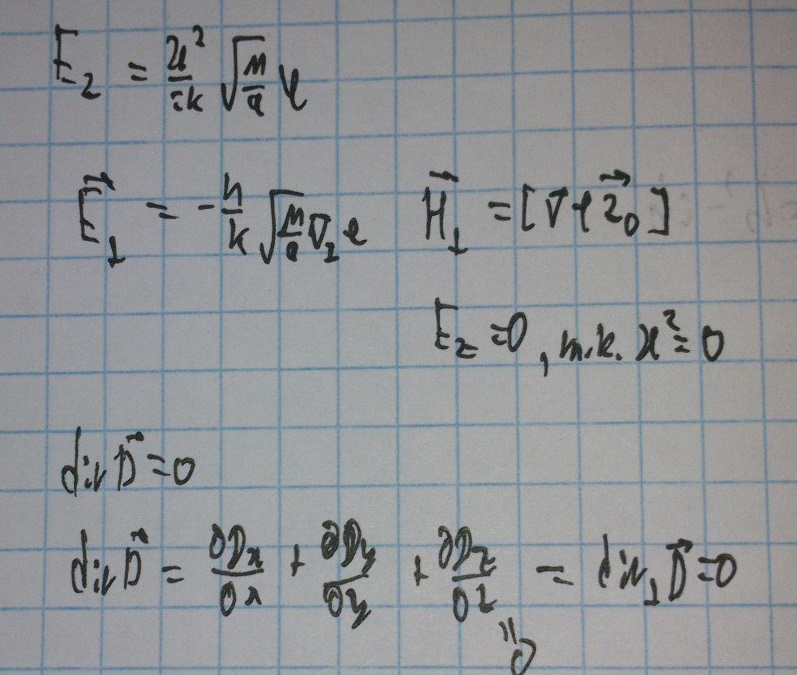
Если ε не зависит от координат, то получим следующее: (подставляем поперечную компоненту электрического поля)

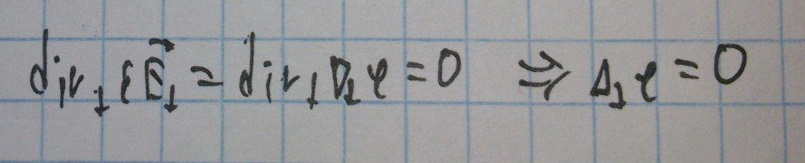
Получили уравнение Лапласа.

Следовательно, электрическое поле будет таким же, как и в статике.

Следствия для ТЕМ-волн:

1. TEM-волны возможны только в тех линиях передач, в которых могут существовать статические поля. От продольной координаты поле не зависит.
2. Структура поля будет такая же, как в статике (под структурой поля подразумевается зависимость от поперечных координат).

Таким образом, ТЕМ волны могут распространяются только в многосвязных волноводах (к примеру коаксиальный волновод - двухсвязный)

Односвязные волноводы  не могут поддерживать TEM-волны.

Рассмотрим две вспомогательные задачи:

Рассчет погонной емкости и индуктивности коаксиального волновода

1) найдем емкость

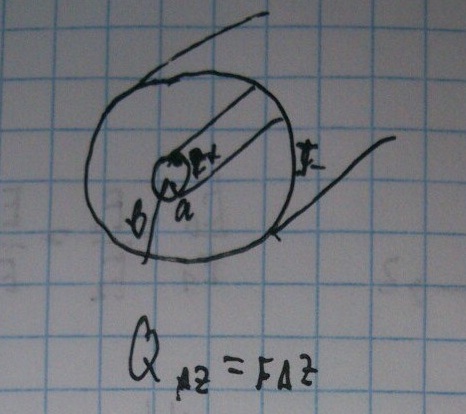
Разместим на центральном проводнике заряд с линейной плотностью

Возьмём участок Δz и исследуем его.

Нужно связать Q и U. Для этого воспользуемся теоремой Гаусса.

(в качестве замкнутой поверхности выберем цилиндрическую, учтем, что электричское поле радиально). 

В итоге получили значение погонной ескости волновода.

2) найдём индуктивность.

(используем теорему о циркуляции)

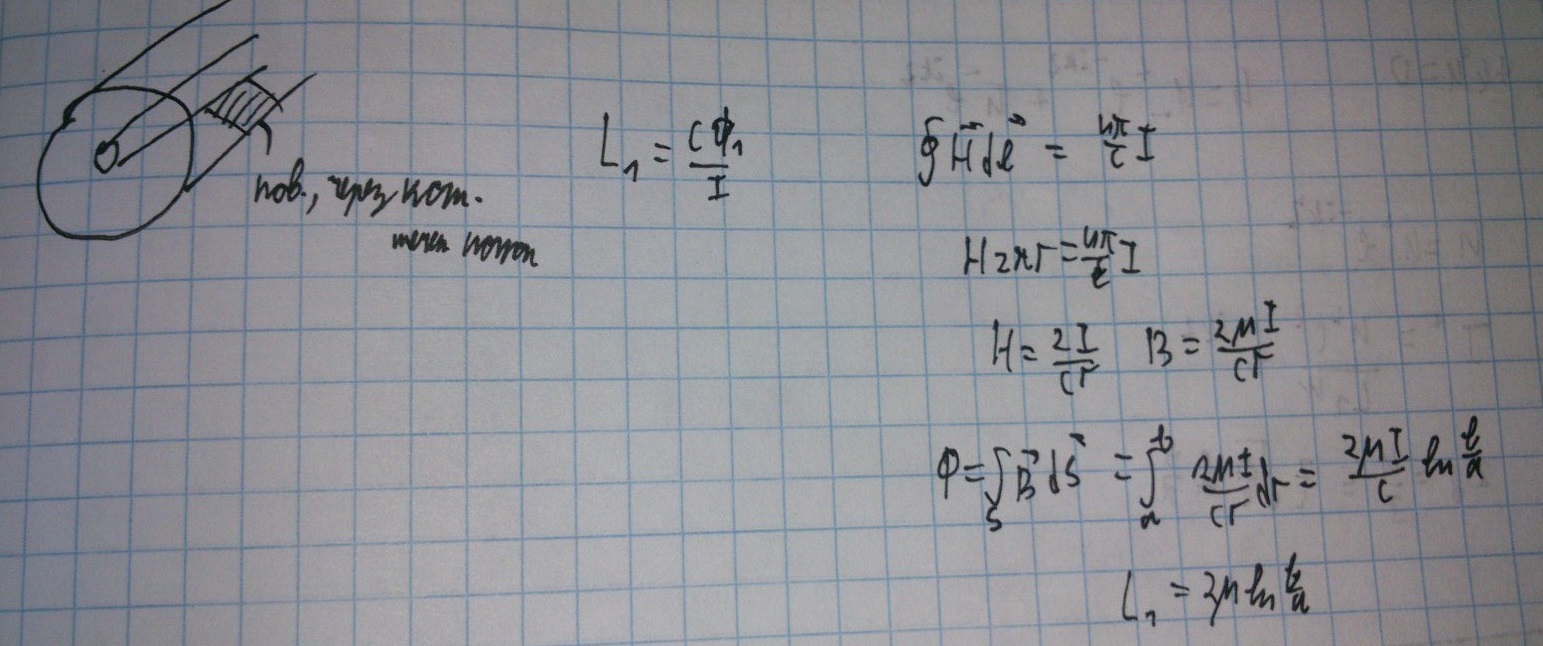
В итоге получили значение погонной индуктивности волновода.

Телеграфные уравнения

Телегра́фные уравне́ния — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи.

Использование телеграфных уравнений, а так же введение скалярных величин для токов и напряжений обусловлено тем, что на практике зачастую удобнее работать именно с ними (выражения для компонент полей несут избыточную информацию). При этом значения этих величин изменяются только вдоль продольной компоненты z и не зависят от формы траектории самой линии. 

Будем считать, что погонные параметры будут совпадать в статике и для TEM-волн.

Получим первое уравнение:

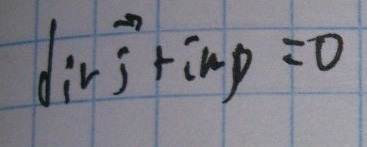
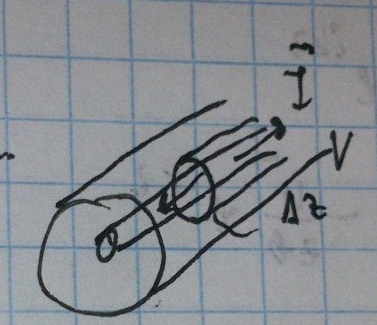
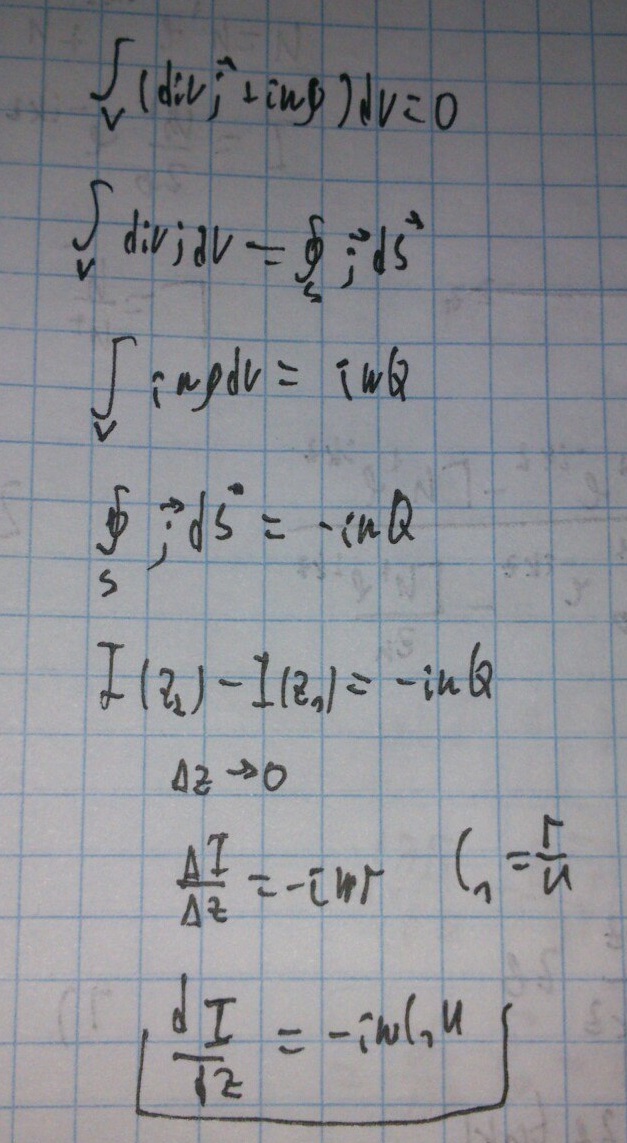 — первое уравнение

Аналогично получим второе уравнение:

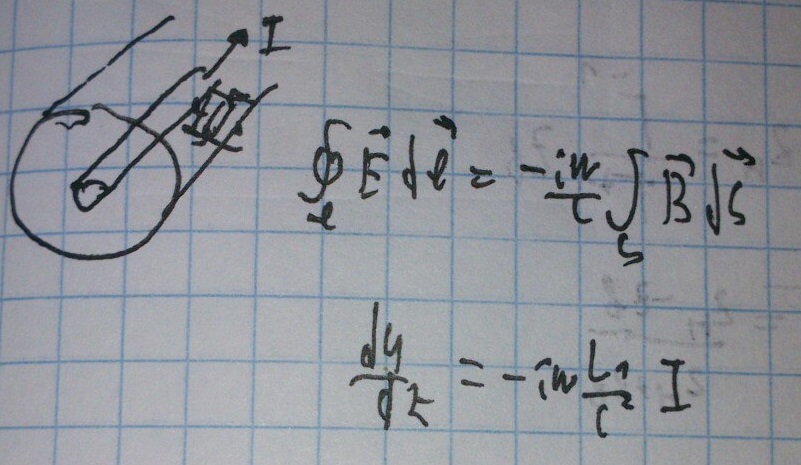— второе уравнение

Теперь объединим их:

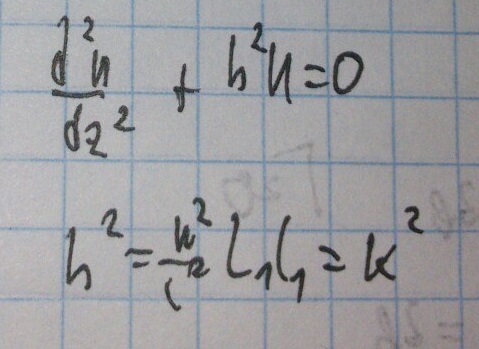
 Тогда получается: