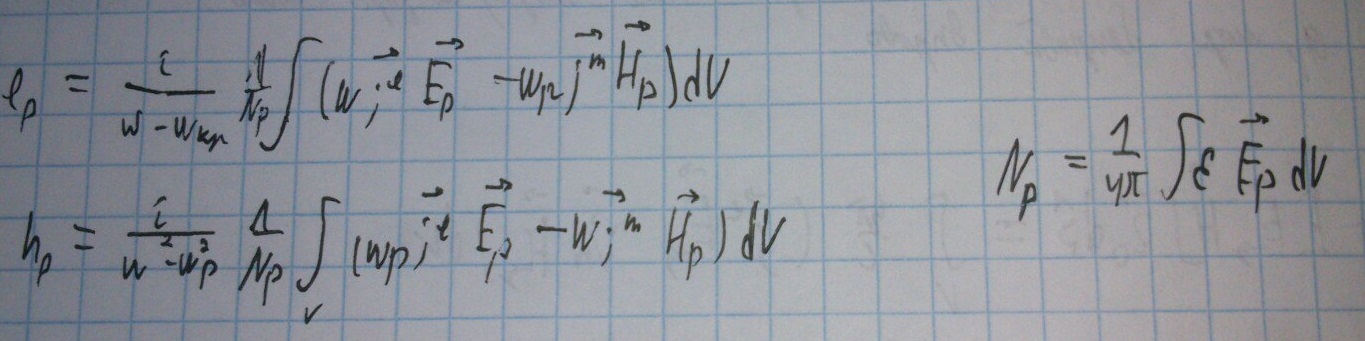Возбуждение волноводов заданными источниками

Ранее мы рассматривали волноводы, в которых волны возбуждаются идеальными источниками.

Однако могут использоваться источники с переменным напряжением.

Подведем такой источник внутрь волновода:

Найдем поля, возбуждаемые заданными токами в волноводе.

В таком случае можем рассматривать поля как сумму мод, возбуждаемых на заданных частотах.

В волноводе существует конечное число распространяющихся волн, значит и эта сумма будет конечной. 

Для того, чтобы составить эту сумму, рассмотрим вспомогательное соотношение:

Лемма Лоренца

Тогда запишем уравнения Максвелла с учётом электрических и магнитных токов:

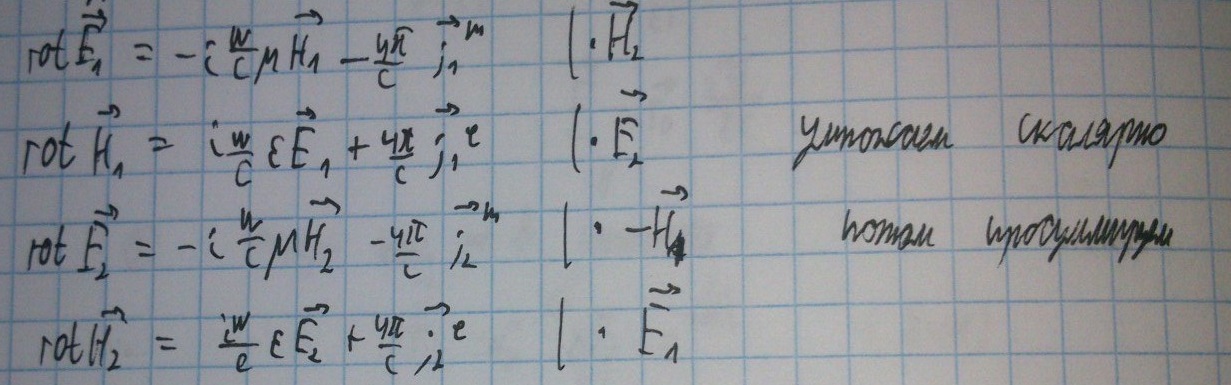
Просуммировав полученные выражения, получаем:

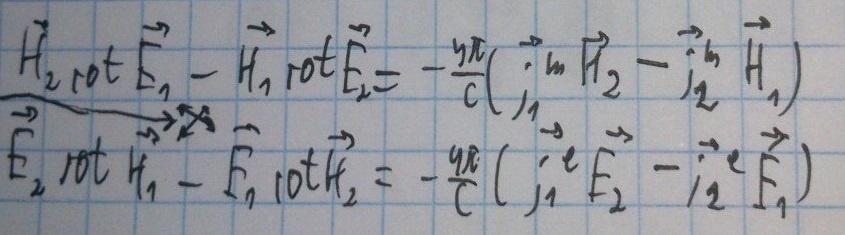
Учтем векторное тождество и применим формулу Гаусса - Остроградского:

Это некий аналог теоремы взаимности, только вместо зарядов и потенциалов лемма Лоренца связывает токи и поля.

Таким образом, зная одно из распределений, мы можем найти другое.

Рассмотрим волновод с идеальными проводящими стенками:

  

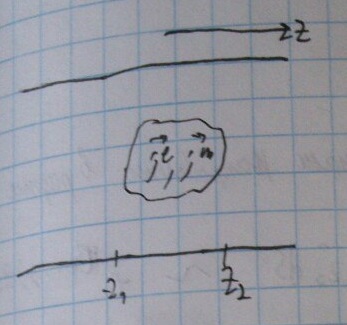
Из физических соображений поля справа — набор мод, бегущих вправо, поля слева — набор мод, бегущих влево.

Обозначим моды как:

Или более общее описание:

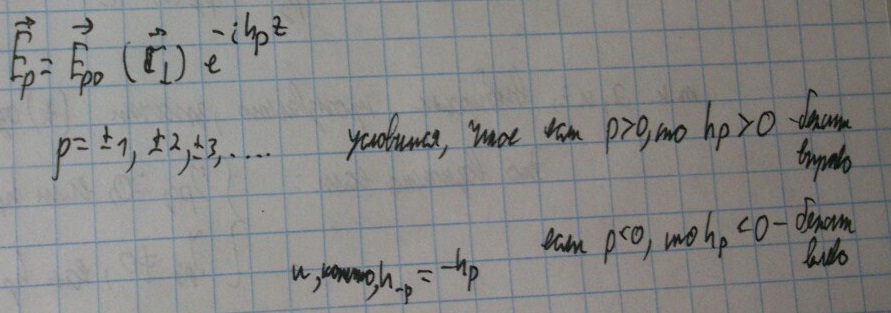
Тогда поля в волноводе можно записать как сумму в следующем виде:

Предположим, что коэффициенты а_p одинаковы для обеих сумм.

Рассмотрим ещё одно вспомогательное соотношение:

Соотношение ортогональности мод волновода

Рассмотрим участок волновода от z₁ до z₂.

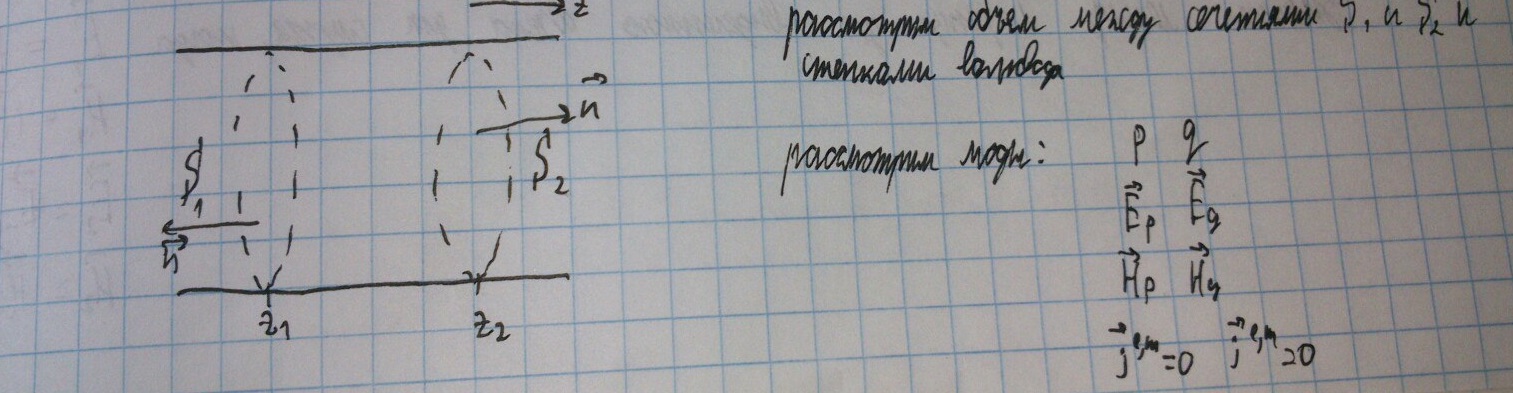
Применим лемму Лоренца:

Заметим, что из граничного условия следует равенство нулю векторного произведения:

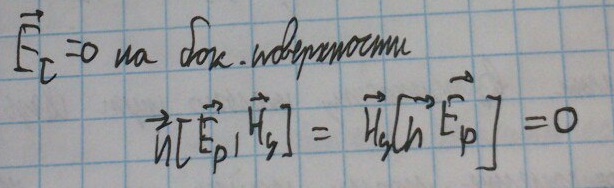
Для второго векторного произведения получаем аналогичный результат, а значит интеграл по боковой поверхности равна 0.

Т.к. по лемме Лоренца интеграл по поверхности равен 0, получается, что интегралы по поверхностям S₁ и S₂ равны по модулю и противоположны по знаку. 

Мы можем обозначить наш интеграл двумя способами:

Т.к. z₁ и z₂ мы вибираем произвольно, то получается, что этот интеграл не зависит от z.

Это возможно, если выполняется соотношение (соотношение ортогональности мод волновода):

 Теперь рассмотрим поля слева и справа источника:

Запишем лемму Лоренца для выделенного объема для случая, когда

 В качестве вспомогательного (эталонного) поля выберем поле моды, бегущей влево.

Тогда мы ищем коэффициенты моды, бегущей вправо:

 

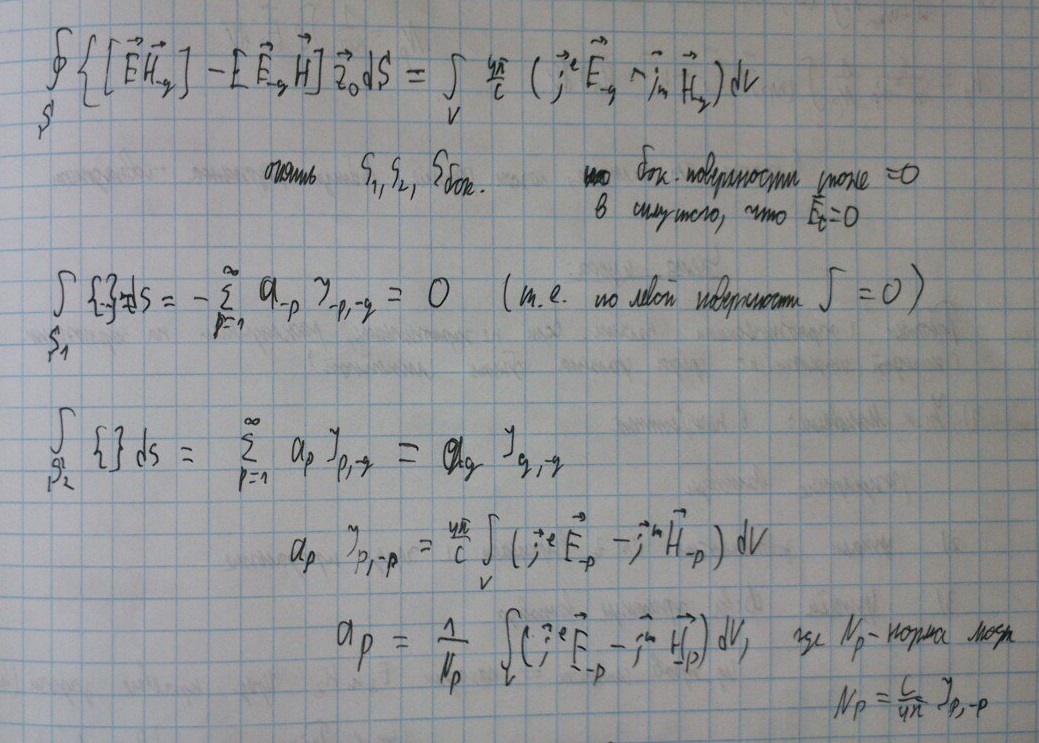
В случае с резонатором, коэффициенты электрического и магнитного полей отличаются.

Они имеют вид: