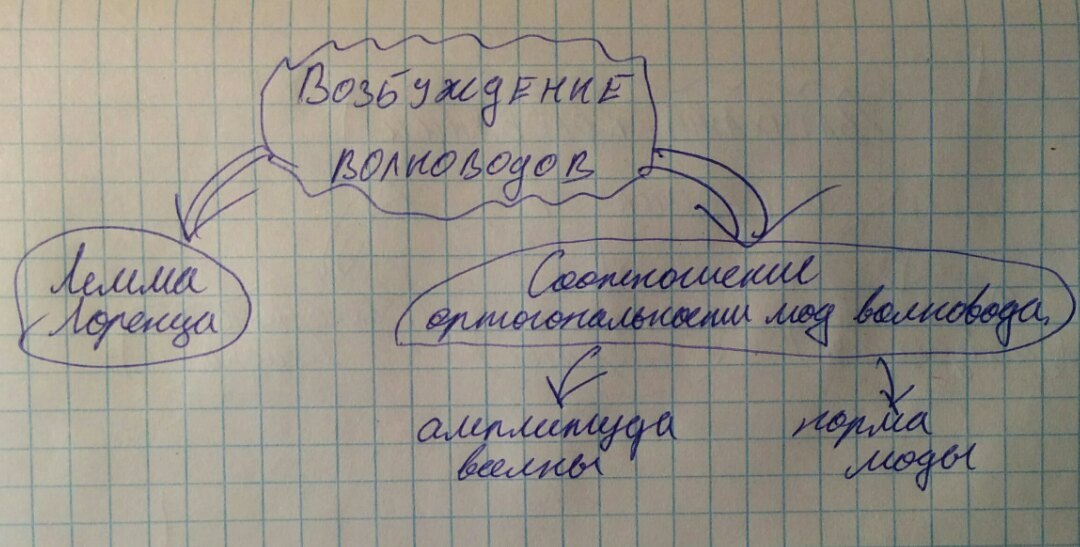

Для того, что бы в реальном волноводе существовали электромагнитные волны, необходимо передать ему энергию, при этом нужно заметить, что поля могут возбуждаться переменными зарядами.
Подведем к волноводу проводник, подключенный к переменному напряжению.
Вследствии чего появятся переменные токи в волноводе, а следовательно появятся поля.
Найдем поля, возбуждаемые заданными токами в волноводе. Поля, которые возбуждаются заданными источниками - это сумма мод волн. Рассмотрим поля, возбуждаемые на заданных частотах. Для этого потребуется вспомогательное соотношение, так как в волноводе существует конечное число распространяющихся мод, следовательно их сумма будет тоже конечной. Таким вспомогательным соотношением является лемма Лоренца.
Рассмотрим в общем случае неоднородное пространство.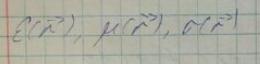
Пусть в нем заданы два распределения тока и соответствующих им распределения поля.
Запишем уравнения Максвелла, в которое входят электрические и магнитные токи. Далее скалярно умножим их на соотвествующие поля.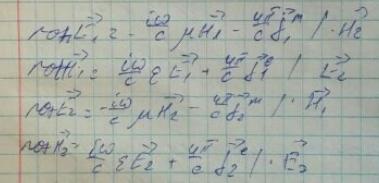
Просуммируем полученные соотношения, тем самым перейдем к двум выражениям: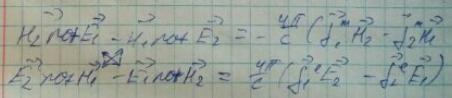
Проссумировав еще раз соответствующие компоненты и применяя равенство: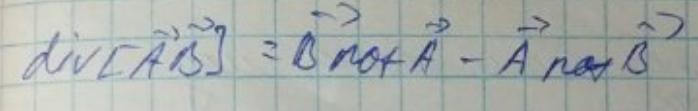
Получим лемму Лоренца в дифференциальной форме:
Проинтегрируем полученное выражение по произвольному объему V, ограниченному поверхностью S и воспользуемся теоремой Гаусса-Остроградского, получая тем самым лемму Лоренца в интегральной форме.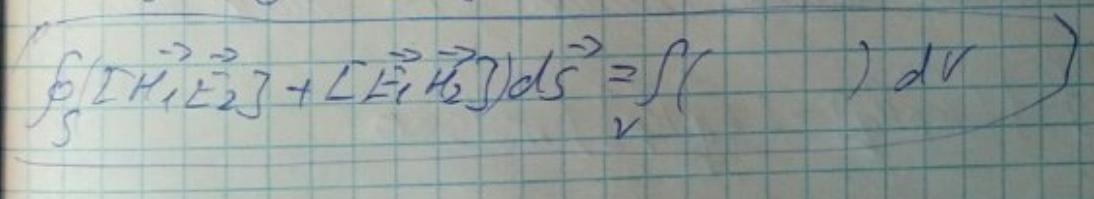
Данная лемма утверждает, что существует связь между токами и соответствующими ими полями.
Можно попробовать найти распределение в какой-либо среде. Тогда, зная одно распределение, можно использовав эту связь, найти второе распределение. Значит существует регулярный метод, позволяющий по одному распределению найти другие распределения.
Перейдем к волноводу.
Если знаем поля без источников (поле моды), то это поле можно применить для нахождения поля возбуждаемого источниками.
Рассмотрим произвольный волновод с идеально проводящими стенками, в котором заданы соответствующие распределения, локализованные в определенной точке пространства. Из визических соображений справа наблюдается набор мод, бегущих вправо, слева набор мод, бегущих влево.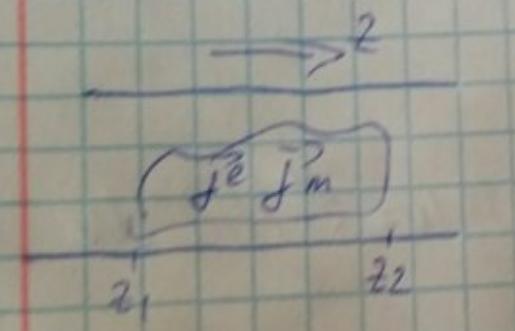
Так как волновод произвольный, обозначим моды через индекс p.
Соответственно существуют поля: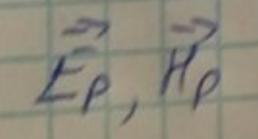
Которые можно записать в виде: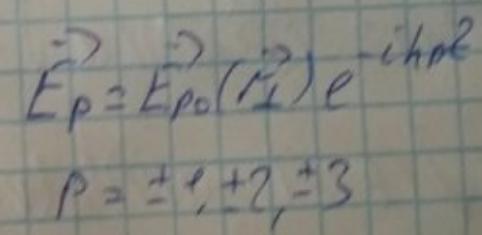
Условимся, если p>0, то hp>0, значит мода бежит вправо.
Если p<0, то hp<0, значит мода бежит влево.
Соответственно можно представить разложение поля по собственным модам: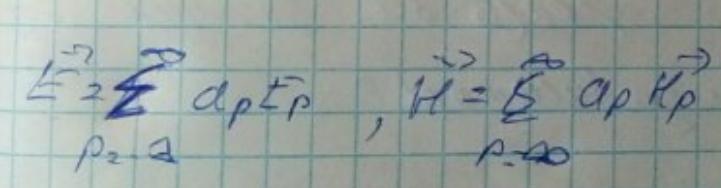
где аp - амплитуда волны с номером p. Будем считать, что она одинаковая для электрического и магнитного полей.
Докажем вспомогательное соотношение, которое носит название - соотношение мод волновода.
Докажем его с помощью леммы Лоренца. Для этого рассмотрим участок волновода от z1 до z2 и введем сечения произвольной формы S1 и S2. Соответственно получили объем, заключенный между стенками волновода и сечениями S1 и S2. Рассмотрим две моды в данном объеме.
Рассмотрим поля, распространяющиеся в данном объеме
И применим к ним лемму Лоренца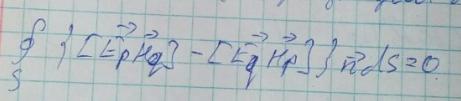
где n - нормаль к поверхности. Поверхность состоит из трех составляющих: боковой поверхности и поверхностей S1 и S2.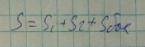
Граничные условия на боковой поверхности имеют вид: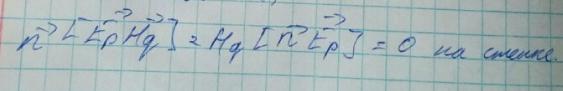
Значит интеграл по боковой поверхности равен 0, следовательно получится выражение: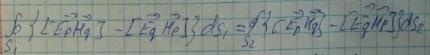
Рассмотрим отдельно интеграл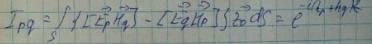
Либо его можно представить в следующей форме: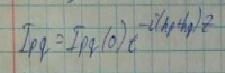
Равенство * означает, что интеграл Ipq не зависит от z, в двух случаях: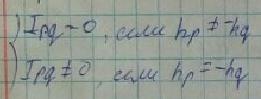
Полученное соотношение называется соотношением ортогональности мод волновода.
Теперь рассмотрим поля, возбуждаемые справа и слева от источника.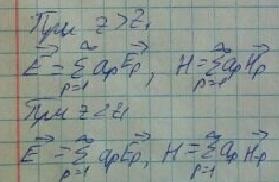
Запишем лемму Лоренца для выделенного объема для следующего случая:
То есть рассмотрим в качестве вспомогательной моды поле моды, бегущей влево. Берем эталонное поле, пускаем его влево, и ищем поле бегущее вправо. С помощью сумм и интегралов достанем ту, которая нам больше нужна.
Рассмотрим интеграл, в котором содержится параметр ap (амплитуда волны с номером p):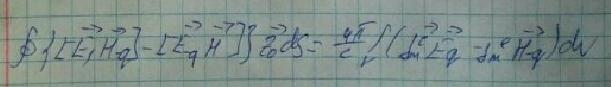
Так как тангенсальная составляющая вектора напряженности электрического поля равна нулю, значит данный интеграл по боковой поверхности тоже равен нулю. Рассмотрим интеграл по боковой поверхности S1 и выразим коэффициенты моды через токи в волноводе: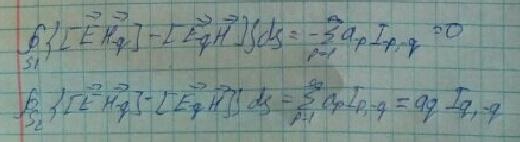

она у моды всегда одна и не зависит от токов.