Оглавление
Телеграфные уравнения — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи. Уравнения были составлены Оливером Хевисайдом, разработавшим в 1880-х годах модель линии электрической связи.
Считаем, что погонные параметры совпадают в статике и для TEM волн.
1. Уравнение для токов.
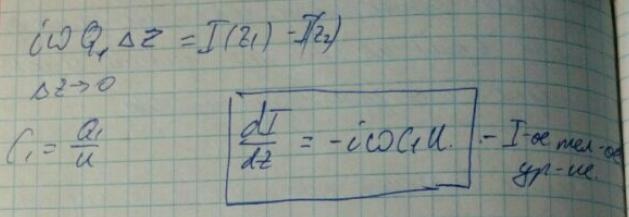
2. Уравнение для напряжений.
Удобнее из двух уравнений прийти к одному.
При этом напряжение в данном случае отличается от статического. Введение скалярных величин для токов и напряжений обусловлено удобством в практическом использовании. При этом их значение изменяется только вдоль продольной компоненты z и не зависит от формы траектоии самой линии.
Решение данного уравнения запишем в виде: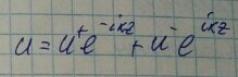
Знак "+" отвечает за компоненту напряжения, направленную вдоль оси z, а знак "-" отвечает за компоненту напряжения, направленную против оси z. Будем работать с волной направленной в положительном направлении z.
Тогда значения напряжения и тока равны: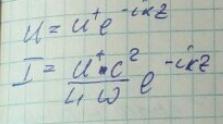
Введем понятие волнового импеданса в бегущей волне: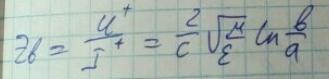
Заметим, что данное выражение зависит от геометрических размеров линии.
Рассмотрим коаксиальную линию.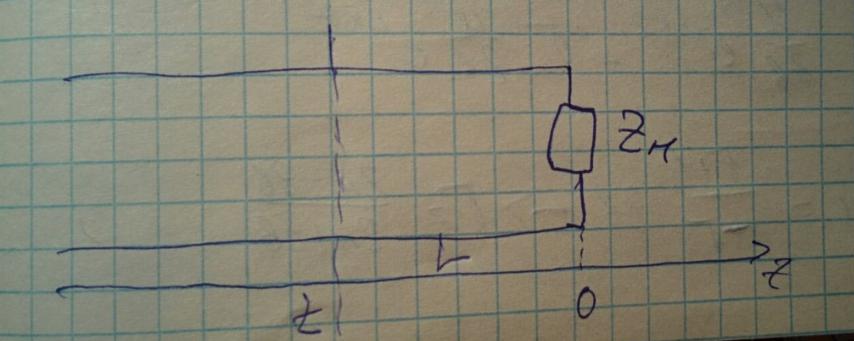
Запишем уравнения для тока и напряжения в ней.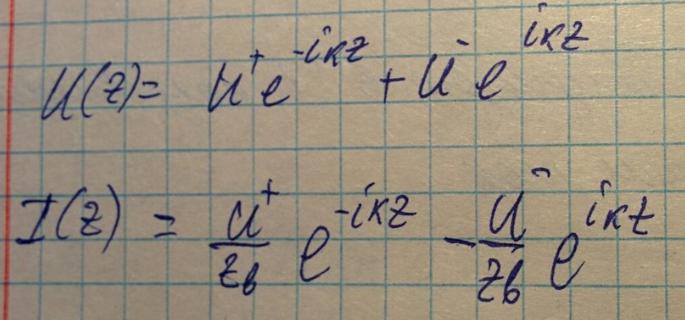
Введем вспомогательную величину, которя называется коэффициентом отражения в сечении z, равное отношению амплитуды отраженной волны, к амплитуде падающей.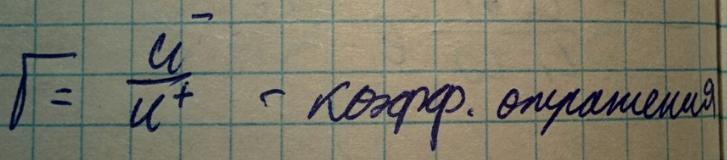
Теперь запишем выражение для импеданса в сечении: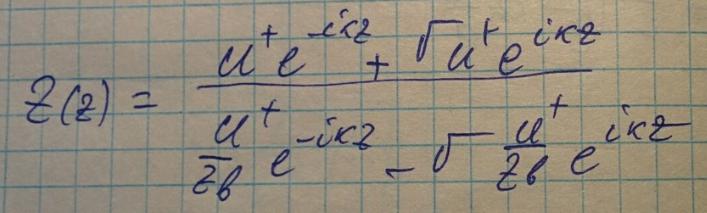
Воспользуемся граничным условием, тоесть то, что импеданс в начале координат равен импедансу нагрузки. Из него выразим коэффициент отражения, которе подставим в значение имеданса в сечении. Получим искомую формулу пересчета импедансов: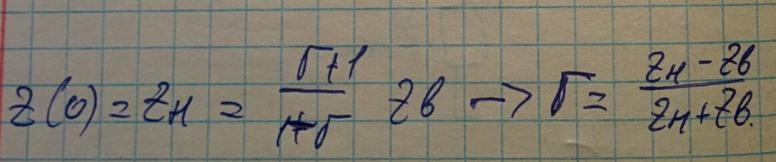
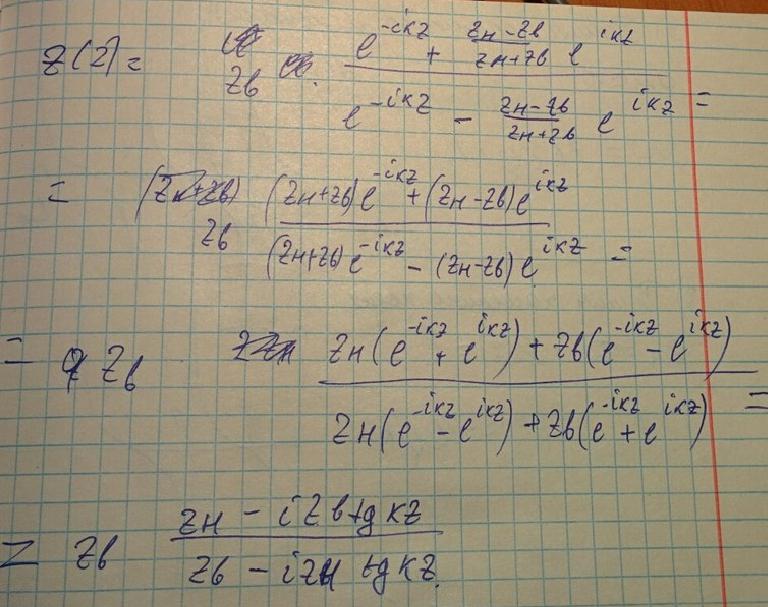
Классическая запись формулы пересчета импедансов имеет вид: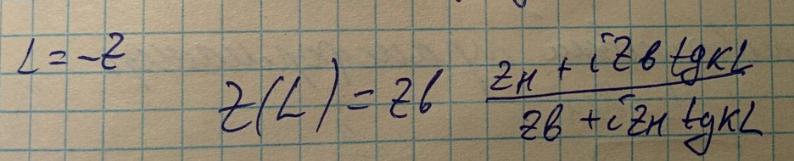
1. Режим согласования.
При данном режиме работы импеданс нагрузки равен волновому сопротивлению, из чего следует что коэффициент отражения равен 0. Значит в данном случае нет встречной волны, которая повышает уровень шума и уменьшает скорость переноса информации. В данном случае вся энергия поглащается нагрузкой.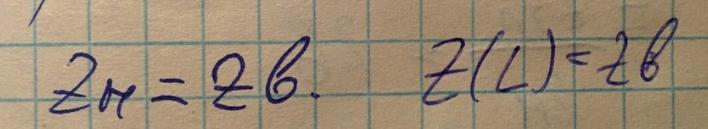
2. Режим короткого замыкания.
При данном режиме работы импеданс нагрузки равен нулю, соответственно коэффициент отражения равен минус единице, а из формулы пересчета импедансов следует: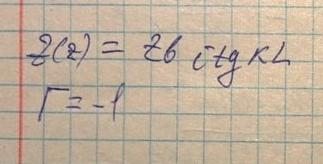
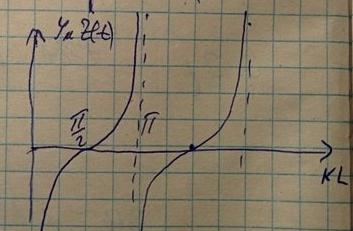
Это означает, что вся энергия отразится от нагрузки и амплитуда падающей волны равна амплитуде отраженной. Закороченная линия позволяет получать реактивный импеданс, что можно проследить по следующему графику: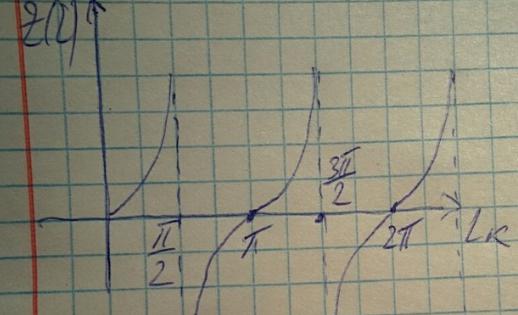
Часть графика, находящаяся выше нуля отвечает за индуктивную нагрузку, а та часть что ниже нуля за емкостную.
3. Режим холостого хода.
При данном режиме импеданс нагрузки равен бесконечности, соотвественно коэффициент отражения равен единице, а импеданс в сечении по формуле пересчета импедансов равен: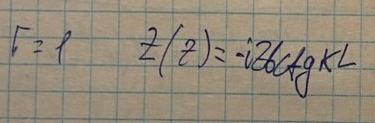
График будет иметь следующий вид: