
Представленная линейка GP2DXX дальномеров Sharp, была разработана не только для обнаружения обьектов на дальних расстояниях, но и для предоставления данных о расстоянии, в случае с моделями GP2D12, GP2D120 и GP2DY0A ('0A'). Эти модели работают намного лучше, так как используются новый метод измерения.
Для определения расстояния либо просто наличия объекта в поле зрения сенсора используется метод триангуляции и малая линейная CCD матрица.
Основная идея в следующем. Импульсы ИК излучения испускаются излучателем. Это излучение распространяется и отражается от обьектов находящихся в поле зрения сенсора. Отраженное излучение возвращается на приемник. Испускаемый и отраженный лучи образуют треугольник «излучатель — обьект отражения — приемник».
Угол отражения напрямую зависит от расстояния до обьекта. Полученные отраженные импульсы собираются высококачественной линзой и передаются на линейную CCD матрицу. По засветке определенного участка CCD матрицы определяется угол отражения и высчитывается растояние до обьекта.
Этот метод более защищен от эффектов интерференции излучения и разной отражающей способности поверхностей, выполненных из различных материалов и окрашенных в различные цвета. Например, стало возможно определение черной стены при ярком освещении.

Общие теоретические сведения о механических колебаниях.
| Уравнение колебаний. Колебания широко распространены в природе. В общем случае под колебаниями понимают движения, в том или иной степени повторяющиеся во времени. По физической природе изменяющейся величины колебательные процессы разделяют на механические, электромагнитные, электромеханические и т.д. Особую роль в физике играют механические и электромагнитные колебания. С помощью распространяющихся колебаний плотности и давления воздуха (воспринимаемых как звук) и с помощью распространяющихся электромагнитных колебаний (свет) мы получаем большую часть информации об окружающем мире. Несмотря на различную физическую природу колебаний, все они обладают некоторой общей сущностью, которая в первую очередь определяется возможностью их единообразного математического описания. Все колебания могут быть разбиты на три группы: периодические, квазипериодические и непериодические. Периодическими колебаниями мы называем те процессы, которые повторяются во времени и описываются такой функцией времени, что f(t)=f(t+T), где Т — период данного колебания. Квазипериодическими колебаниями называются такие непериодические колебания, которые в течение длительного времени сохраняют основные характеристики процесса при медленном изменении их параметров (например, амплитуды). Если уравнения, описывающие колебания, имеют вид линейных дифференциальных уравнений, колебания называются линейными. Физически это соответствуют тем случаям, когда в системе все возникающие силы можно считать линейными функциями координат и скоростей. Колебательный процесс в системе может возникнуть в двух случаях. В первом из них за счет внешней силы система выводится из состояния устойчивого равновесия, т.е. ей сообщается некоторое достаточное количество потенциальной или кинетическоэй энергии, после чего внешние силы полностью отключаются. Тогда, за счет работы внутренних сил, образующихся в ситеме, происходит переход кинетической энергии в потенциальную и наоборот. В этом случае возникают колебания, которые называются свободными или собственными колебаниями системы. Если же на систему постоянно действует внешняя сила, то возникают так называемые вынужденные колебания. Если физическая величина x(t) изменяется со временем по гармоническому закону |
 (1) (1) |
колебания называются гармоническими. Здесь А — амплитуда колебаний; 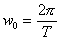 — круговая частота (T — период); t — время; — круговая частота (T — период); t — время; 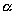 0 —начальная фаза колебаний. Функция х{t) из (1) представляет решение дифференциального уравнения 0 —начальная фаза колебаний. Функция х{t) из (1) представляет решение дифференциального уравнения |
 (2) (2) |
| называемого уравнением свободных колебаний. Физическую систему, выведенную из состояния равновесия и представленную самой себе, в которой изменение одного из параметров х описывается дифференциалльным уравнением (2) называют классическим гармоническим осциллятором. Действие классического гармонического осциллятора на примере пружинного маятника показана ниже. В апплете можно изменять следующие параметры А - амплитуда колебаний или начальное отклонение, m - масса маятника и k - коэффициент жесткости пружины. Стоит так же отметить, что в нашей модели, следующие начальные условия: t=0 , v(0)=0 , x(0)=A, как и в лабораторной работе. Кроме функции x(t), можно наблюдать v(t), a(t) .
Обсудим реализацию гармонического осциллятора на примере пружинного маятника. Собственные колебания пружинного маятника. Пружинный маятник состоит из тела массы m и легкой пружины с коэффициентом жесткости k (рис.1, а). В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси. Для того, чтобы маятник совершал только вертикальные колебания достаточно оттянуть тело строго вниз на небольшую величину (рис.1, б,в ). Для полного описания колебаний в этом случае необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. На тело, подвешенное на пружине в поле силы тяжести действуют две силы (без учета сил трения) сила тяготения и упругая сила. Начало координат выберем таким образом, чтобы при х=О масса mнаходилась в равновесии. При этом сила тяжести mg будет скомпенсирована некоторым начальным растяжением пружины и в дальнейшем рассмотрении участвовать не будет. При отклонении тела от точки равновесия будет возникать возвращающая сила F(х). Рассмотрим малые колония пружинного маятника. Колебания пружиннного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смешению и направлена в сторону положения равновесия. Для пружиннного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука. Уравнение движения пружинного маятника при этом имеет вид |
 (3) (3) |
Сравнивая с (2), имеем 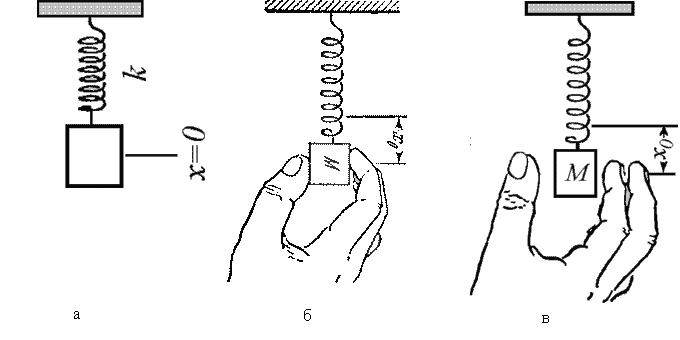 |
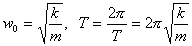 (4) (4) |
В реальных осцилляторах, за счет сил трения, происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. При движения тела пружинного маятника в вязкой среде, с небольшими скоростями сила трения пропорциональна скорости 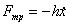 . При учет диссипации энергии уравнение колебаний пружинного маятника имеет вид линейного дифференциального уравнения второй степени . При учет диссипации энергии уравнение колебаний пружинного маятника имеет вид линейного дифференциального уравнения второй степени |
 (5) (5) |
Решение этого уравнения имеет вид затухающих колебаний |
 (6) (6) |
где X10 , 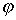 10 — начальные амплитуда и фаза колебаний, w — частота затухающих колебаний, 10 — начальные амплитуда и фаза колебаний, w — частота затухающих колебаний, 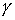 — декремент затухания. Действительно, подставим (6) в (5) получим — декремент затухания. Действительно, подставим (6) в (5) получим |
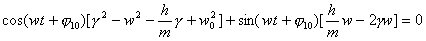 (7) (7) |
Отсюда следует, что |
 (8) (8) |
Используя полученный результат уравнение колебаний удобно записать в виде: |
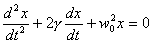 (9) (9) |
Отклонения маятника от положения равновесия в зависимости от времени в соответствии с (6) имеет вид показанный на рис. 2,a. Для малых декрементов затухания колебания близки к гармоническим, при больших 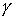 затухание происходит за 1—2 периода. В том случае, когда затухание происходит за 1—2 периода. В том случае, когда 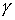 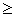 w0 значение частоты w становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс—тело маятника после начального отклонения плавно возвращается в положение равновесия (см. рис.2, б), w0 значение частоты w становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс—тело маятника после начального отклонения плавно возвращается в положение равновесия (см. рис.2, б), Величина  получила название декремента затухания. При этом величина получила название декремента затухания. При этом величина 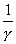 равна времени, за которое амплитуда колебаний затухает в е раз. Затухание колебаний за период равна времени, за которое амплитуда колебаний затухает в е раз. Затухание колебаний за период  = =  Т носит название логарифмического декремента затухания, его можно определить из соотношения Т носит название логарифмического декремента затухания, его можно определить из соотношения 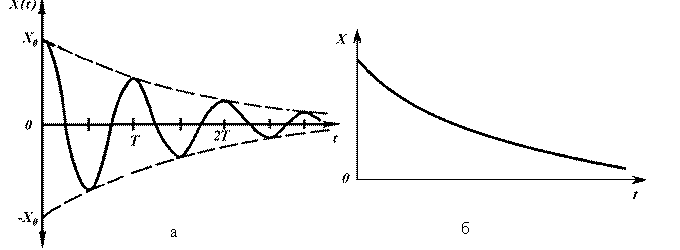 |
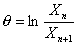 (10) (10) |
где 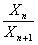 — отношение амплитуд двух последовательных колебаний. — отношение амплитуд двух последовательных колебаний. Вынужденные колебания пружинного маятника. Рассмотрим теперь колебания пружинного маятника, которые возникают под действием внешней периодической силы Fвн(t) 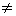 0 в системе с одной степенью свободы. Вынужденные колебания в случае гармонического воздействия описываются уравнением 0 в системе с одной степенью свободы. Вынужденные колебания в случае гармонического воздействия описываются уравнением |
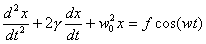 (11) (11) |
где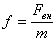 — нормированная амплитуда вынуждающей силы, w — частота вынуждающей силы. Решение уравнения (11) имеет вид — нормированная амплитуда вынуждающей силы, w — частота вынуждающей силы. Решение уравнения (11) имеет вид |
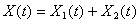 (12) (12) |
| где Х1(t) — решение однородного уравнения (при нулевой правой части), оно соответствует затухающим собственным колебаниям, a Х2(t) — частное решение, соответствующее вынужденным колебаниям на частоте вынуждающей силы |
 (13) (13) |
| где |
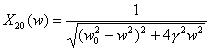 (14) (14) |
зависящая от частоты амплитуда вынужденных колебаний,  (w) — зависящая от частоты фаза колебаний, причем (w) — зависящая от частоты фаза колебаний, причем |
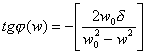 (15) (15) |
Выражения для амплитуды и фазы колебаний, также как и для свободных колебаний, можно определить, непосредственной подстановкой (13) в (11). При малых декрементах затухания на частотах вблизи частоты w  w0 свободных колебаний маятника амплитуда колебаний резко воозрастает. Это явление получило название резонанса. Более точно значение резонансной частоты wрез можно получить из (14), проводя исследование функции на экстремум w0 свободных колебаний маятника амплитуда колебаний резко воозрастает. Это явление получило название резонанса. Более точно значение резонансной частоты wрез можно получить из (14), проводя исследование функции на экстремум |
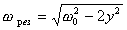 (16) (16) |
В этом апплете представлены вынужденные колебания пружинного маятника. Этот случай, как было сказано выше, описывается уравнением (11). Важная особенность этого случая заключается в том, что менять частоту вынуждающей силы, то можно добиться резонанса. Так же вы можете наблюдать установление вынужденных колебаний.
Типичные амплитудно—частотные и фазочастотные характеристики показании на рис.3 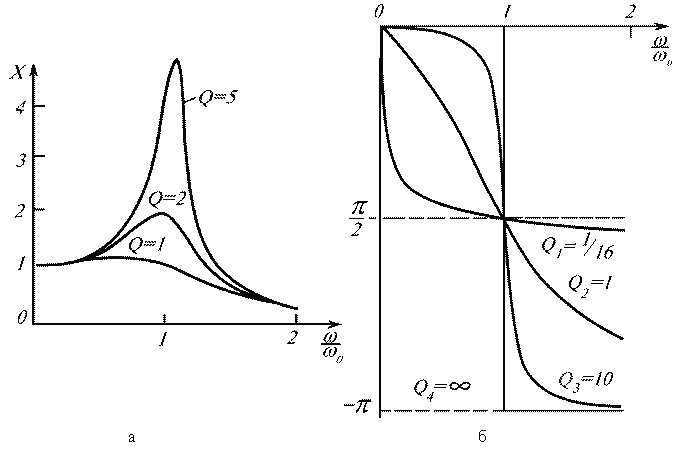 Семейство амплитудно-частотных характеристик u - относительная амплитуда смещения c - относительная амплитуда скорости w - относительная амплитуда ускорения Q - декремент затухания кнопка "старт" запускает апплет, кнопка "+" позволяет к нарисованным графикам добавлять другие. Кнопка "сброс" позволяет нарисовать новое семейство графиков при других параметрах.
 При анализе резонансных кривых в системах с различным затуханием наряду с декрементом затухания При анализе резонансных кривых в системах с различным затуханием наряду с декрементом затухания 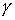 , логарифмическим декрементом затухания , логарифмическим декрементом затухания 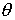 широко пользуются величиной , которая называется добротностью системы Q. Она определяется как отношение амплитуды смещения при резонансе ( w = w0 ) X2рез к амплитуде смещения Xcт при широко пользуются величиной , которая называется добротностью системы Q. Она определяется как отношение амплитуды смещения при резонансе ( w = w0 ) X2рез к амплитуде смещения Xcт при 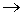 0. Учитывая определения коэффициента затухания, логарифмического декремента затухания, а также соотношение (14), получаем 0. Учитывая определения коэффициента затухания, логарифмического декремента затухания, а также соотношение (14), получаем |
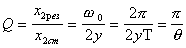 (17) (17) |
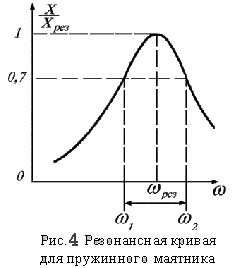
Можно показать, что в случае, когда Q > 1 добротность можно выразить также через ширину резонансной кривой (см.рис.4) |
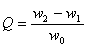 (18) (18) |