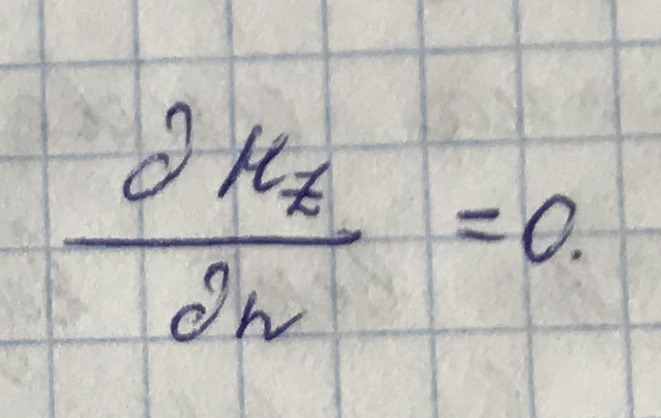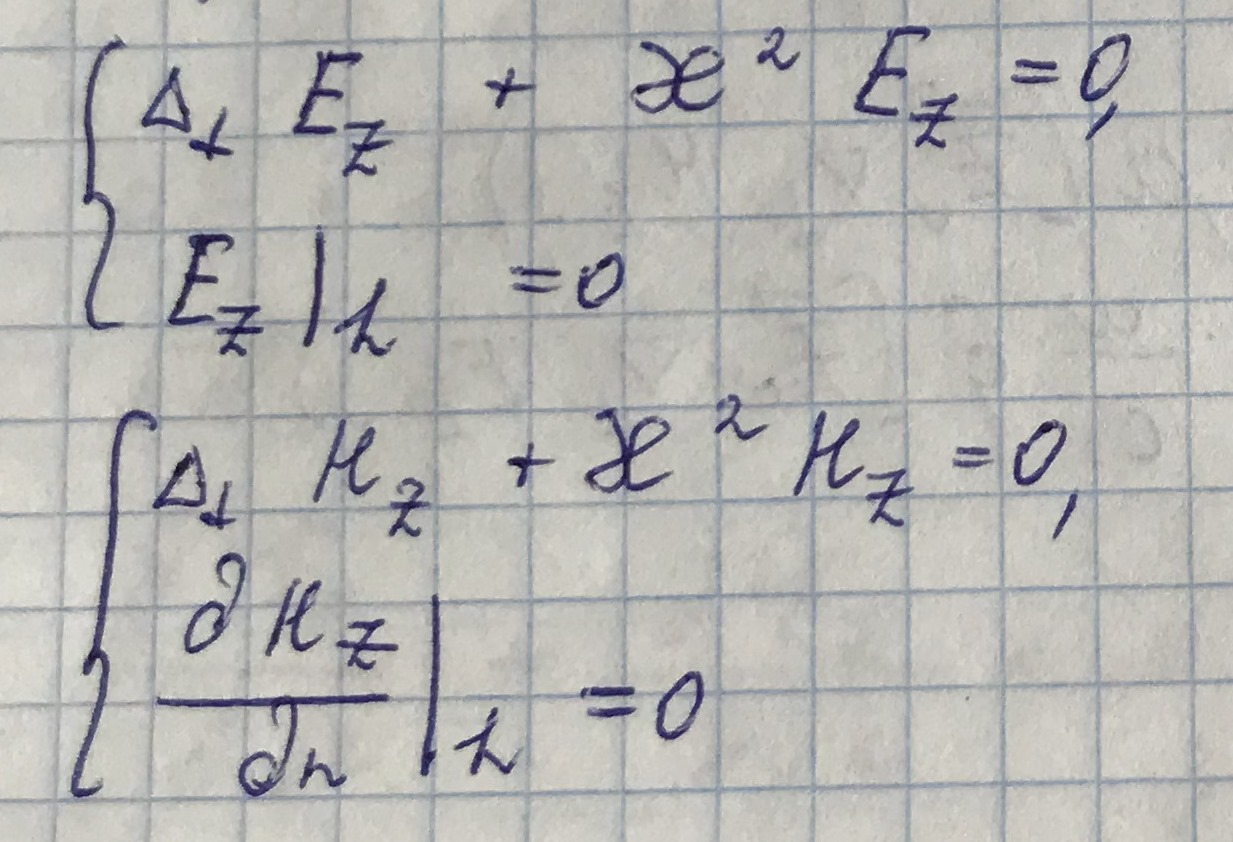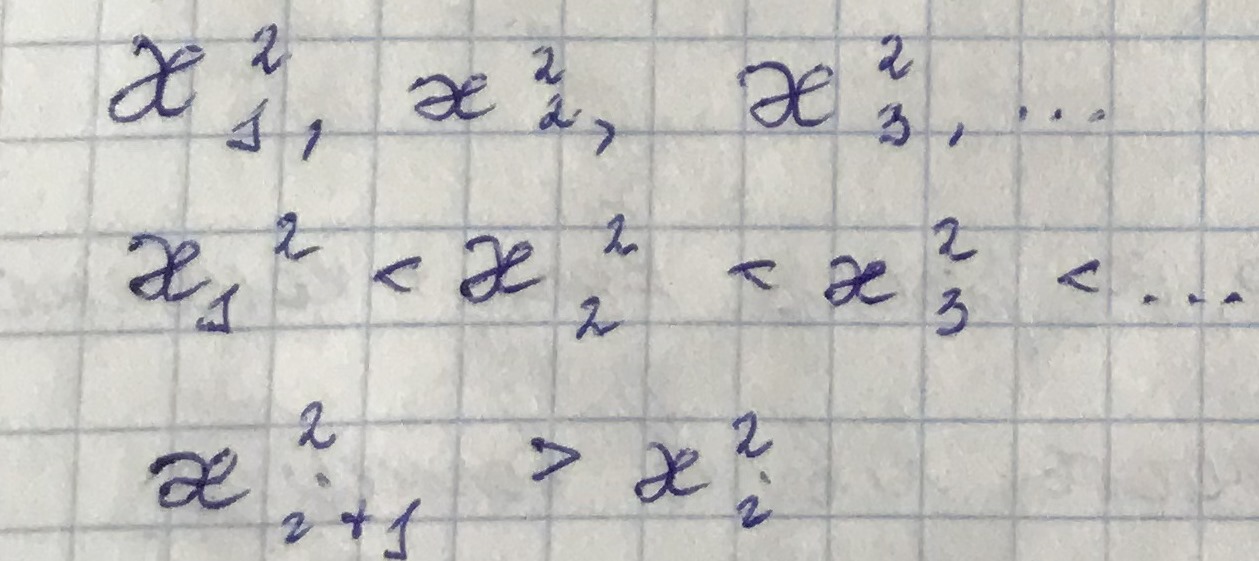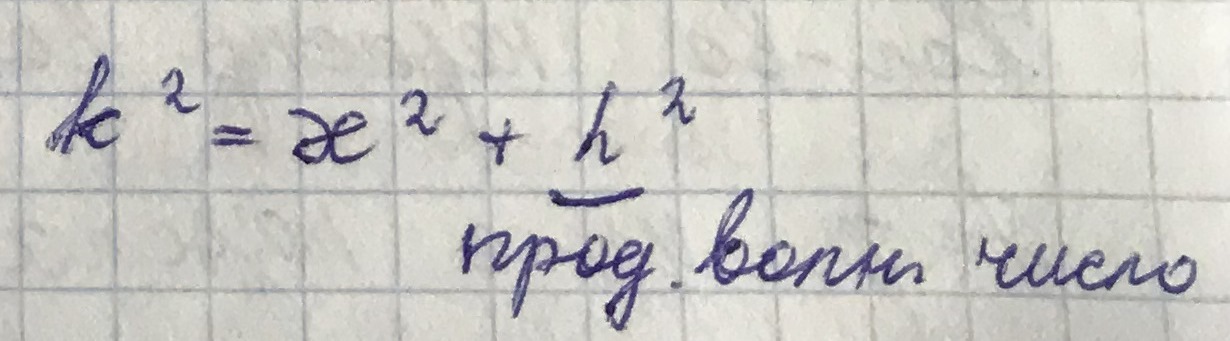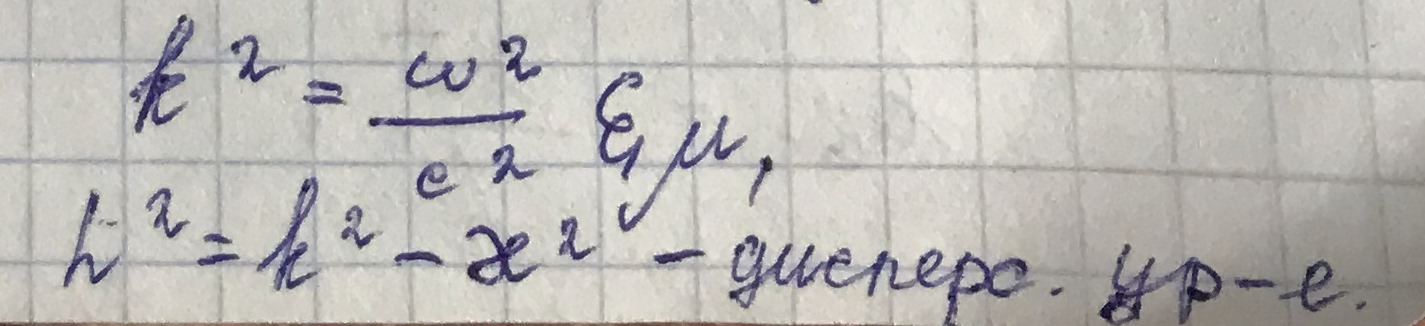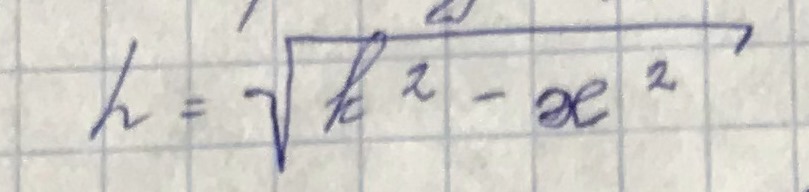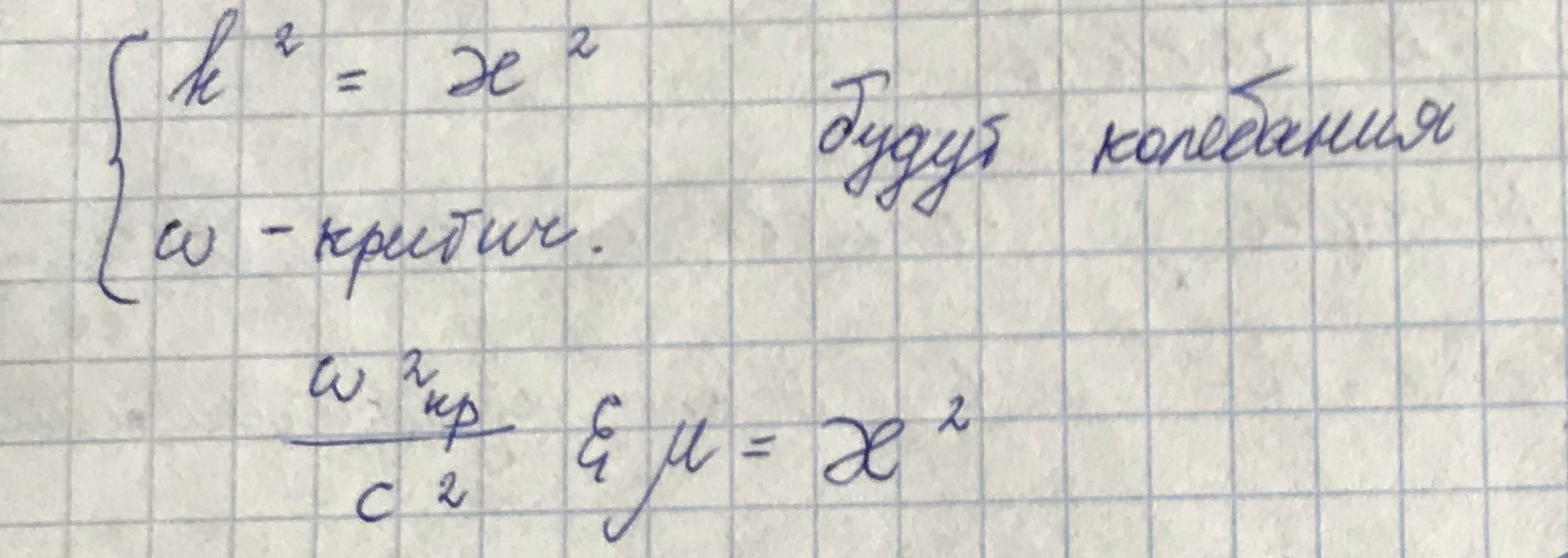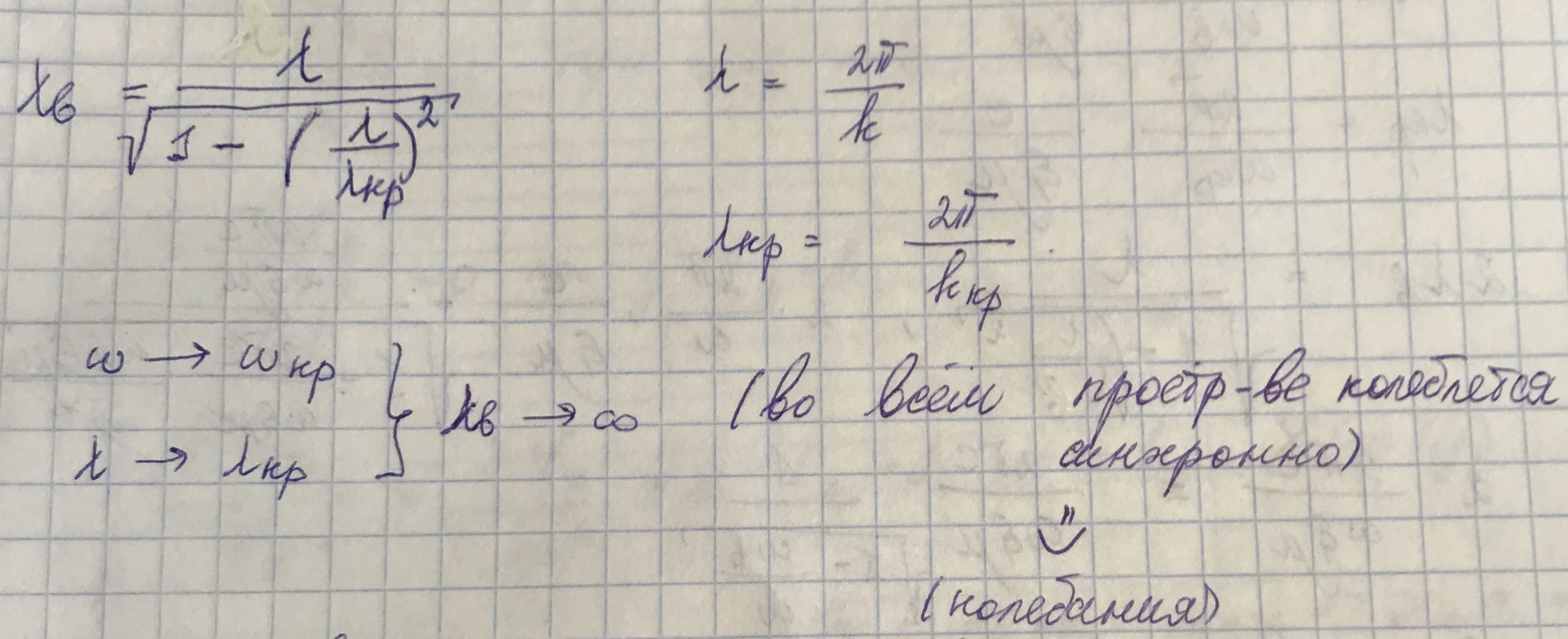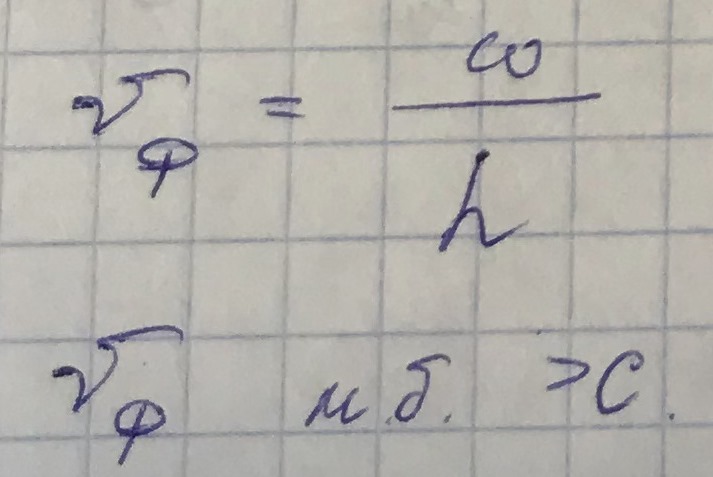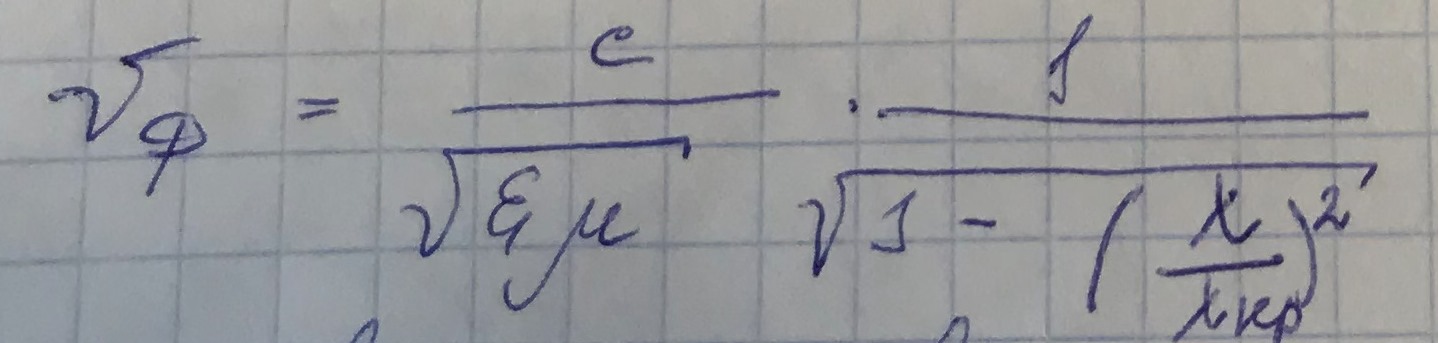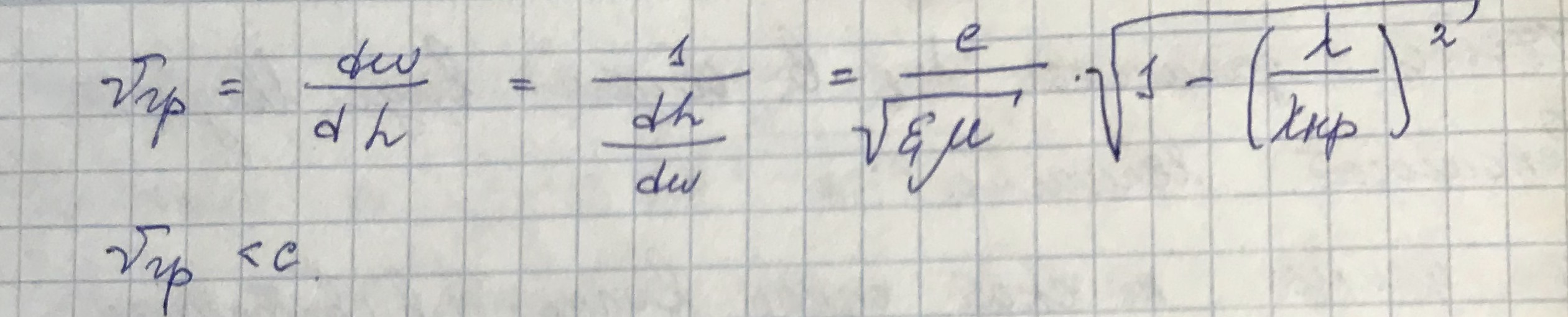
Выполнила Молева Александра, группа 437.
2019 год
2.1. Понятие регулярных волноводов.
Регулярные волноводы - волноводы, свойства которых не меняются или меняются периодически вдоль направления распространения волны.

Учитывая это условие, запишем уравнения Максвелла для комплексных амплитуд:
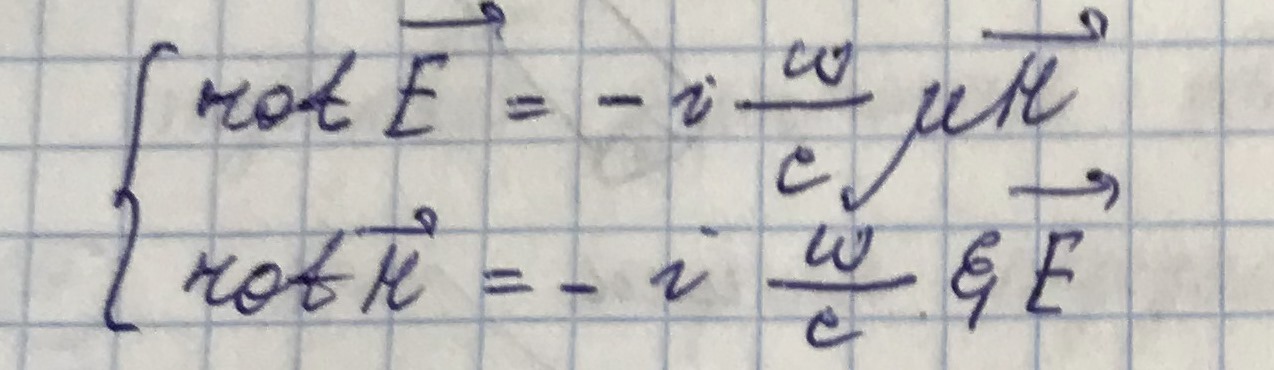
Поля будут иметь вид:
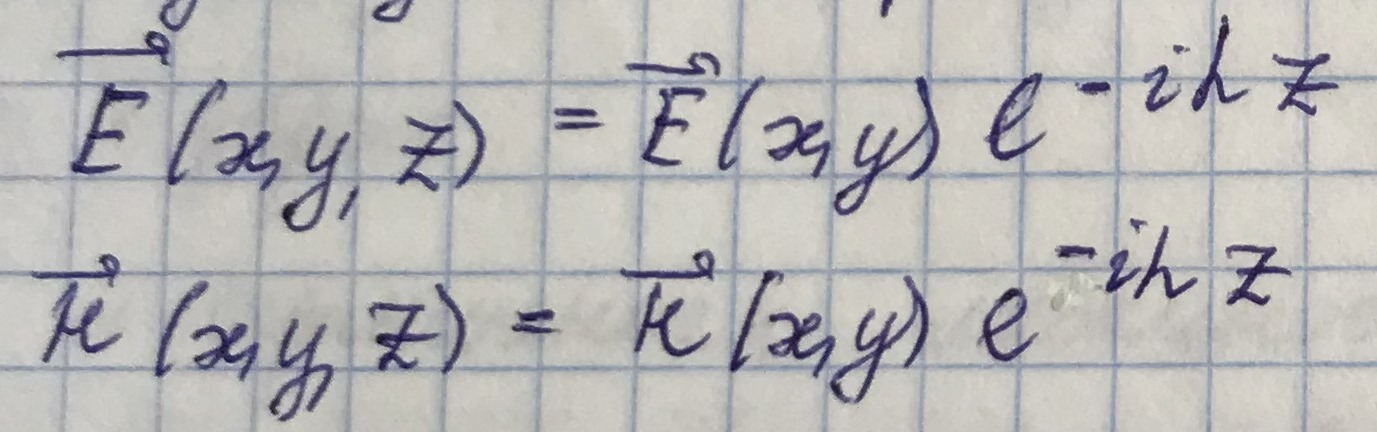
Подставим уравнения для элекрического и магнитного полей в уравнения Максвелла для комплексных амплитуд и запишем их в декартовой системе координат.
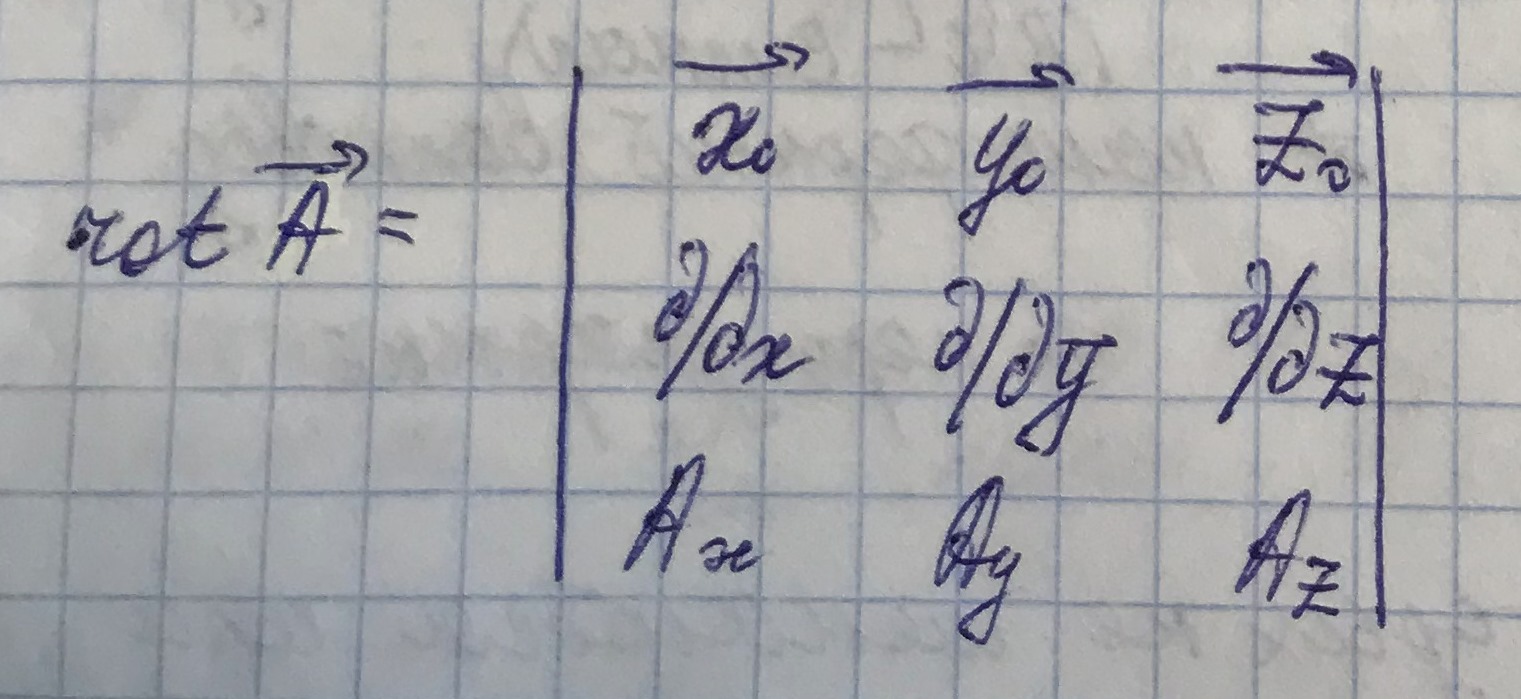
В результате взятия ротoра получаем следующие выражения для проекций электрического и магнитного полей:

Сгруппируем уравнения согласно стрелкам:
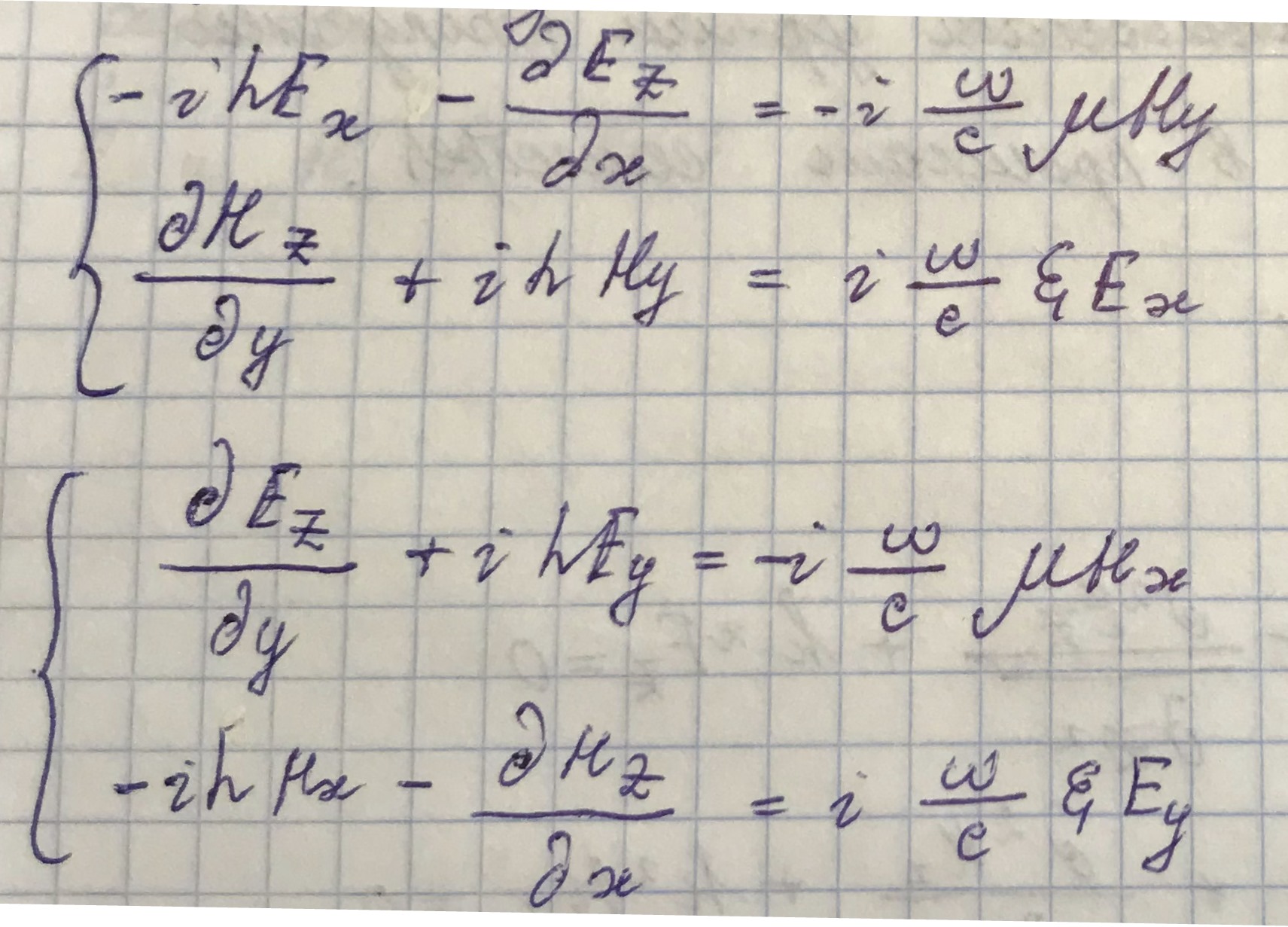
Последовательно решая системы уравнений, выразим поперечные координаты полей через продольные:
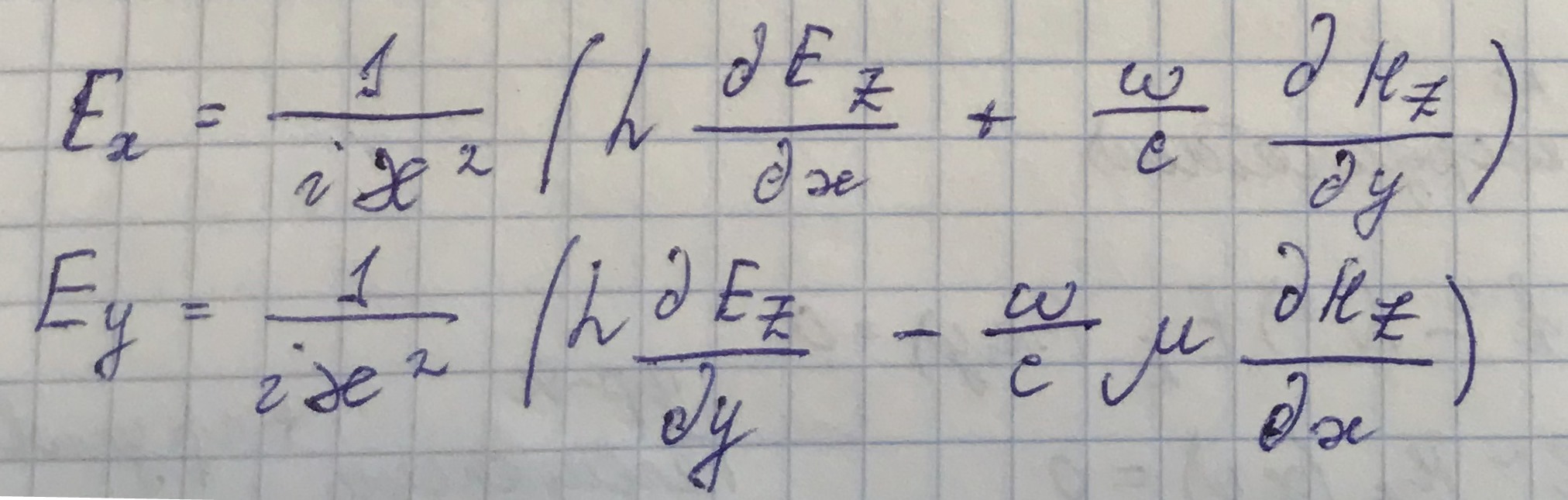
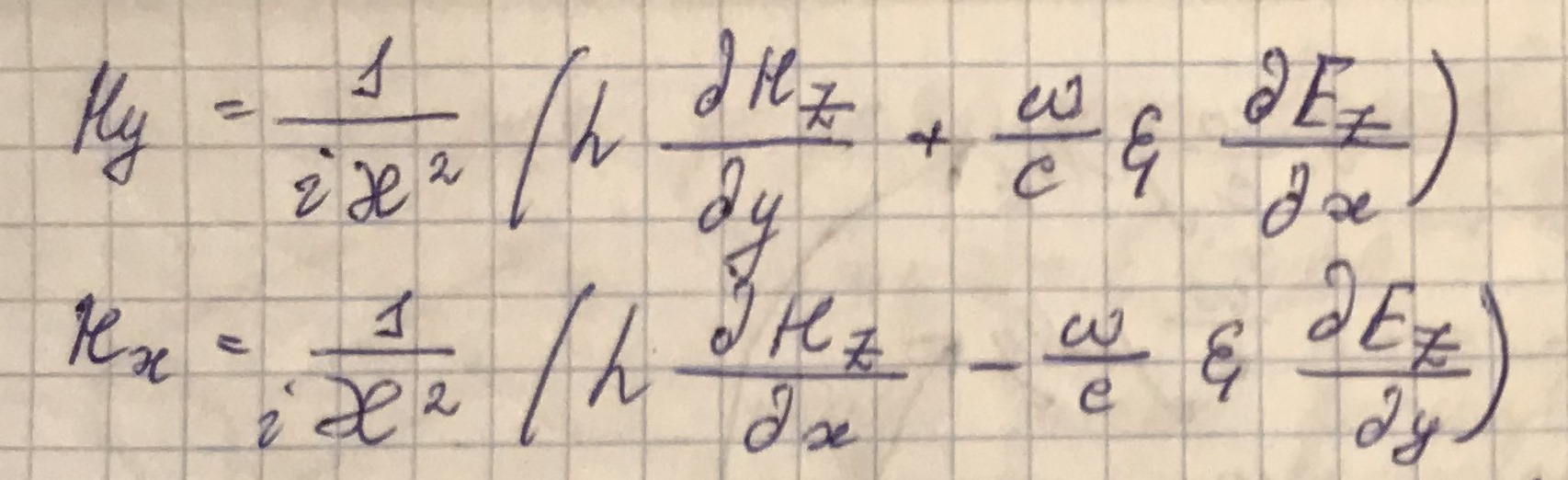
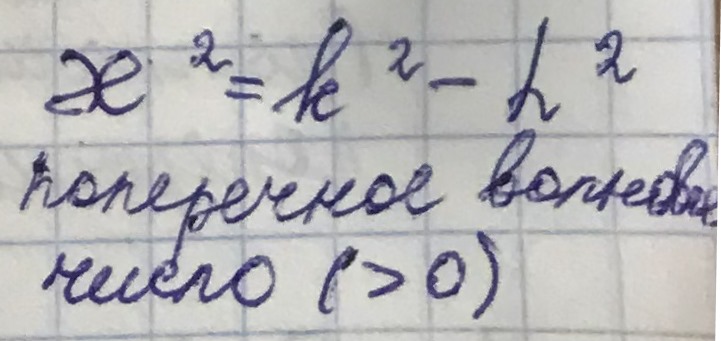
До предположения о регулярности волновода необходимо было считать, что нам неизвестно в волноводе 6 скалярных функций, а после предположения стало 2 неизвестных скалярных функций.
Для нахождения компонент полей 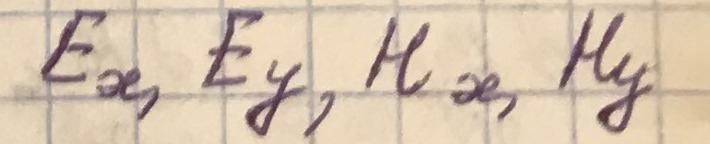 воспользуемся волновыми уравнениями (получены из уравнений Максвелла в прошлом семестре):
воспользуемся волновыми уравнениями (получены из уравнений Максвелла в прошлом семестре):
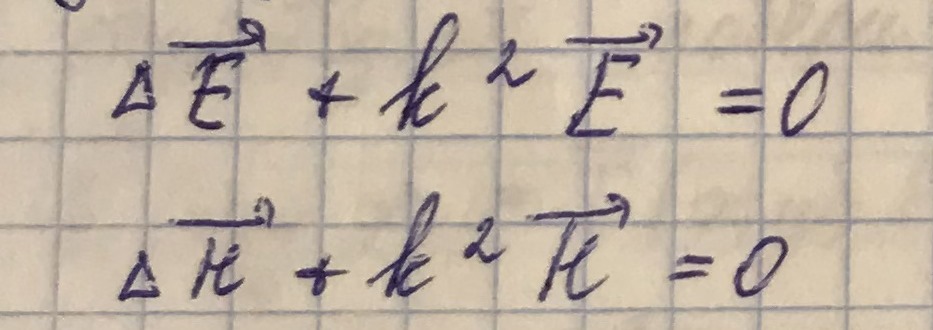
Распишем те же уравнения, разложив лапласиан по поперечным координатам:

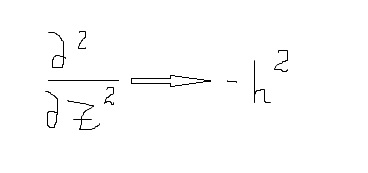 Учитывая это условие, запишем:
Учитывая это условие, запишем:
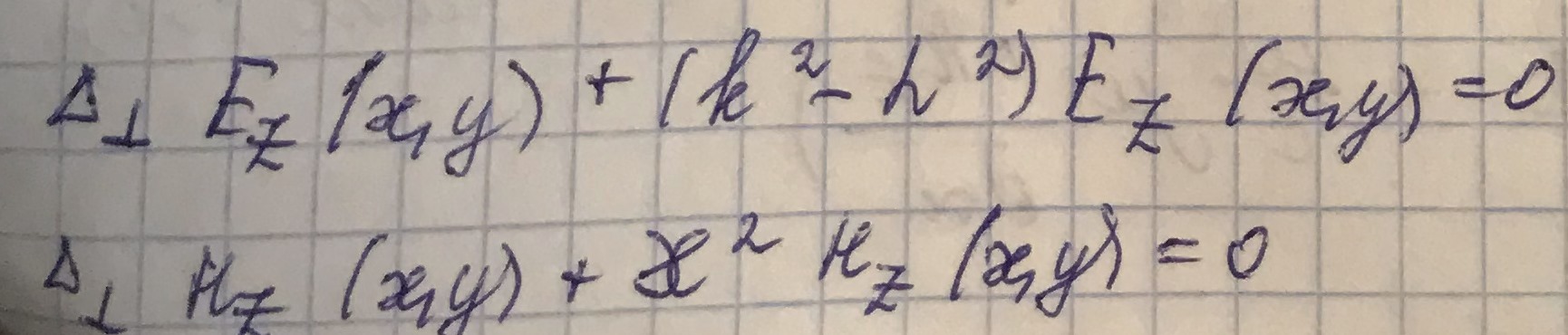
Получили уравнения Гельмгольца - эллиптические дифференциальные уравнения в частных производных. Для решения этих дифференциальных уравнений необходимо задать граничные условия:
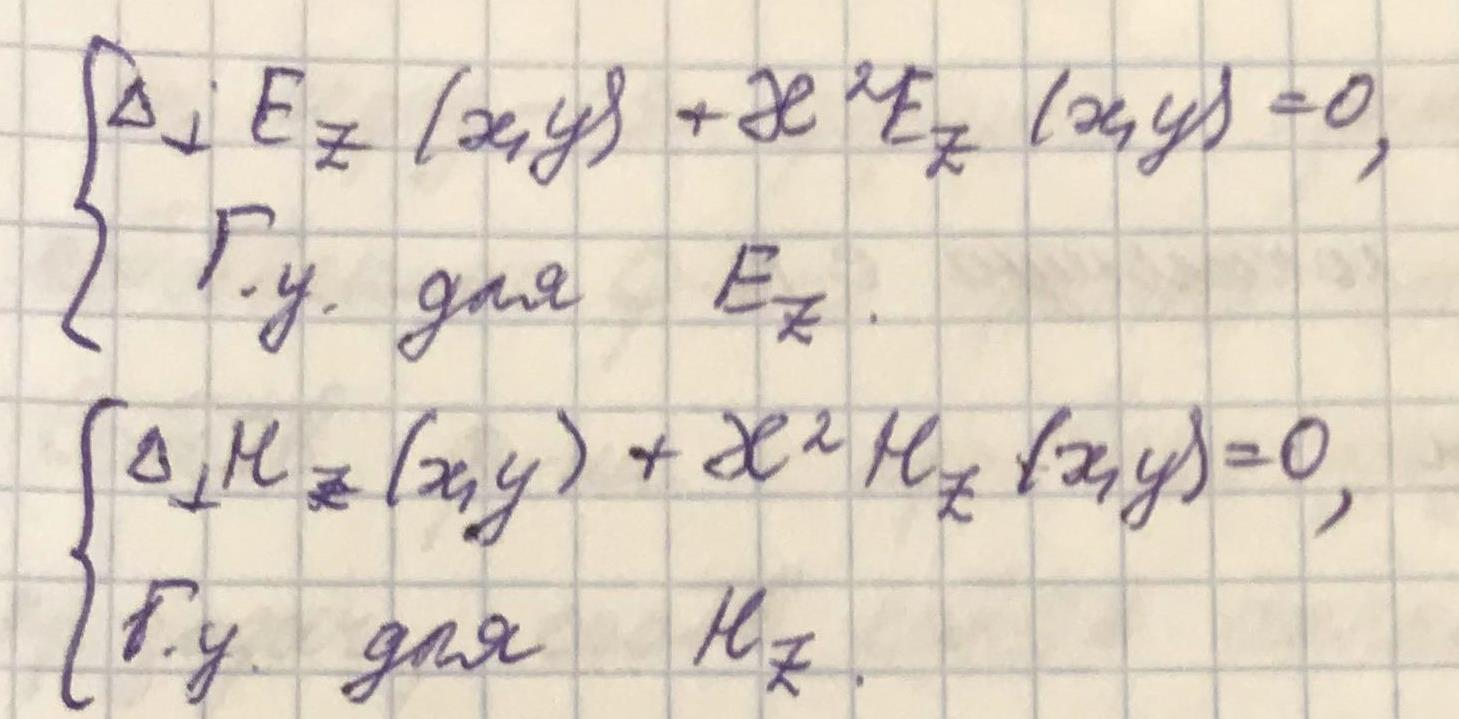
Будем считать, что границы волновода - идеально проводящие стенки, форму пока не определяем.
Запишем теперь на основе компонентного представления поперечные компоненты полей в векторном виде:
2.2. Краевые задачи.
Введем локальную систему координат.
Тогда для тангенциальной компоненты электрического поля получим выражение:
Из условия
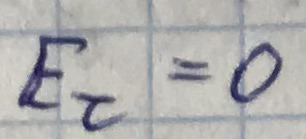
получим:
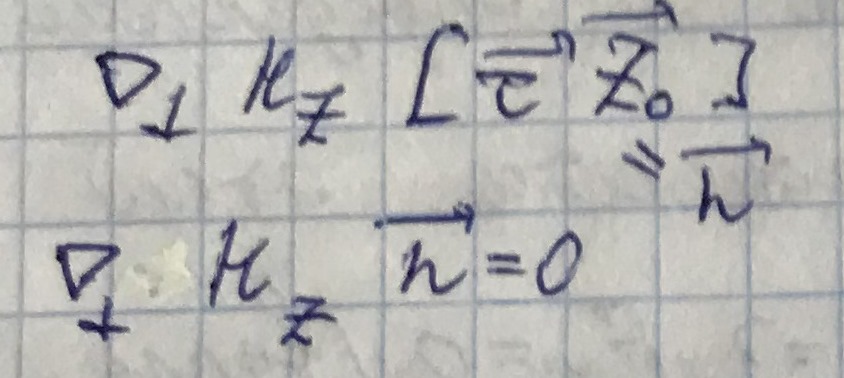
>>
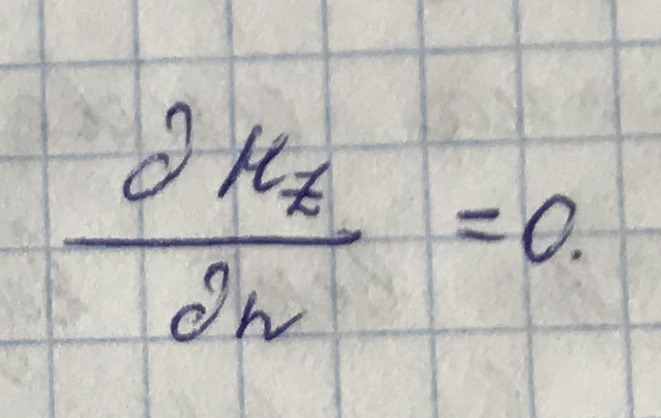
Таким образом, возникают две краевые задачи:
В мат. физике такие задачи - задачи на собственные числа и собственные функции. Решение этих краевых задач возможно не для любых значений поперечного волнового числа
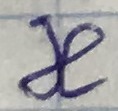
, а для определенных, при которых возможны решения - собственные числа.
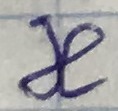
определяется формой границ; найденные
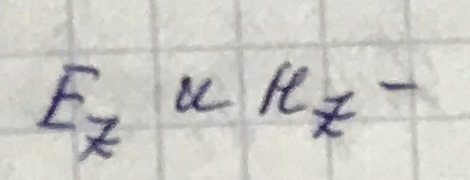
собственные функции краевых задач.
Свойство: В случае, когда границы у волновода идеально проводящие, краевые задачи для
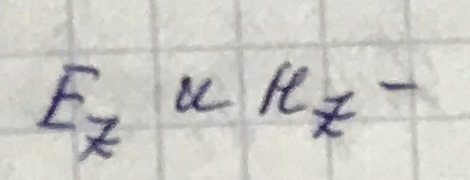
являются независимыми. Следовательно, могут существовать два независимых решения:
1) Если
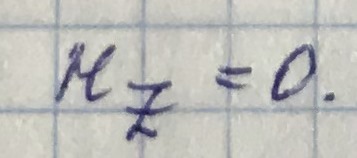
, то имеем дело с поперечно-магнитными волнами (ТМ -, Е - волнами)
2) Если
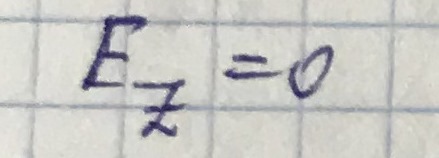
, то волна поперечно-электрическая (ТЕ -, Н - волнами)
Из мат. физики также известно, что решение этих краевых задач возможно для бесконечного числа дискретных значений
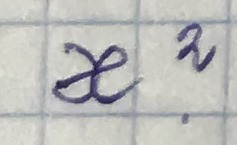
2.3. Дисперсионное уравнение.
Запишем уравнение для электрического поля волны:
Выразив квадрат продольного волнового числа, получим дисперсионное уравнение:
Оно показывает, чему будем равнятся h при изменении частоты:
Волна будет распространяться, когда
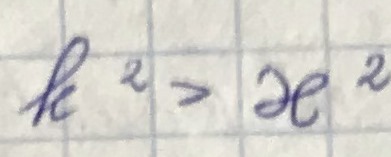
, то есть h - действительное число.
Каждой
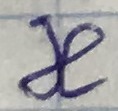
соответствует своя волна, а у каждой волны есть своя критическая частота. Причем:
Волны волновода соответствуют конкретной
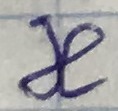
- моде волновода.
Дисперсионное уравнение позволяет получить длину волны в волноводе.
Чтобы записать
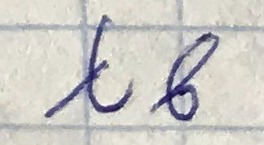
общем виде, введём вспомогательные величины:
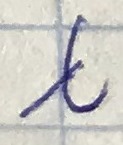 - длину плоской однородной волны в свободном пространстве,
- длину плоской однородной волны в свободном пространстве, 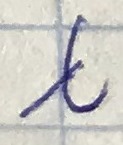 соответствует
соответствует 
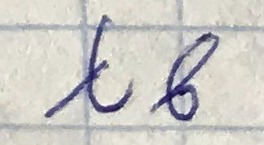 - длину волны в свободном пространстве, соответствующую критической частоте (критическую длину волны),
- длину волны в свободном пространстве, соответствующую критической частоте (критическую длину волны), 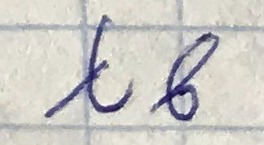 соответствует
соответствует 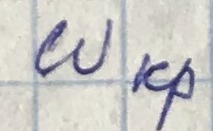 .
.
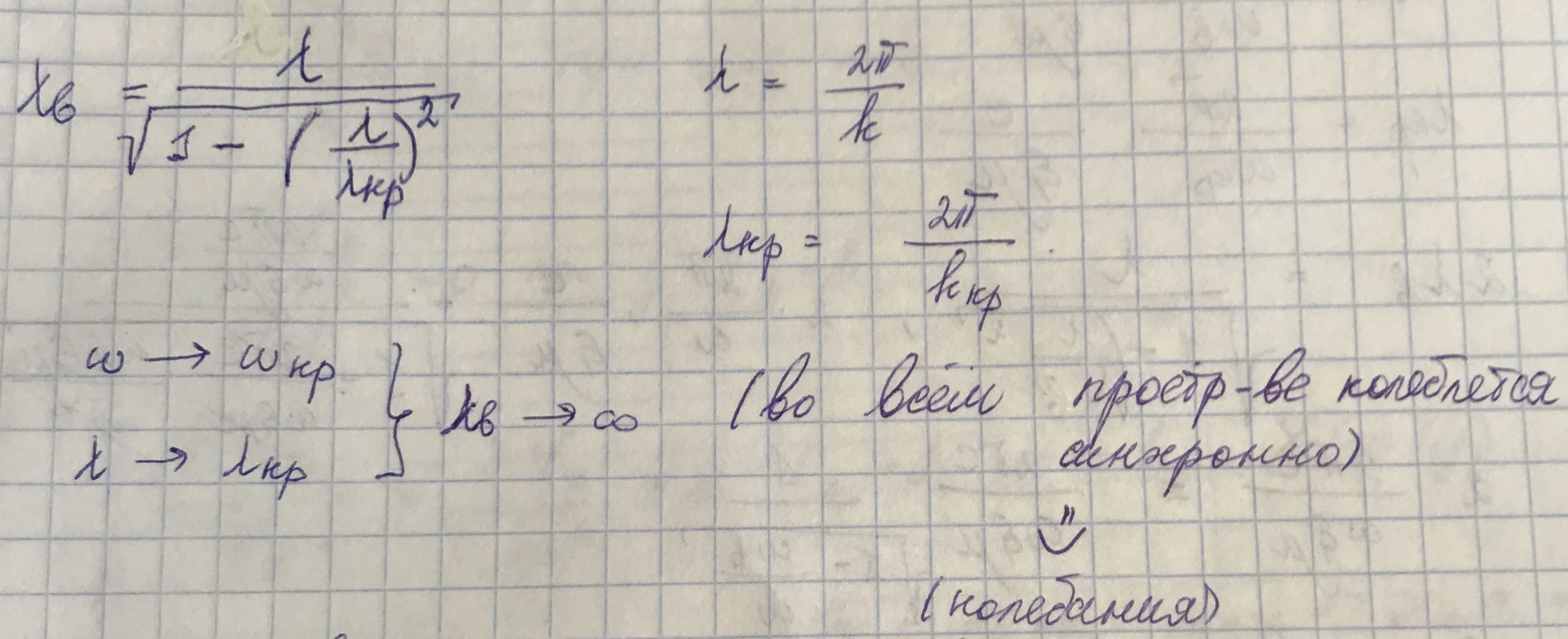
Но в волноводах происходят затухания.
2.4. Фазовая и групповая скорости.
Фазовая скорость:
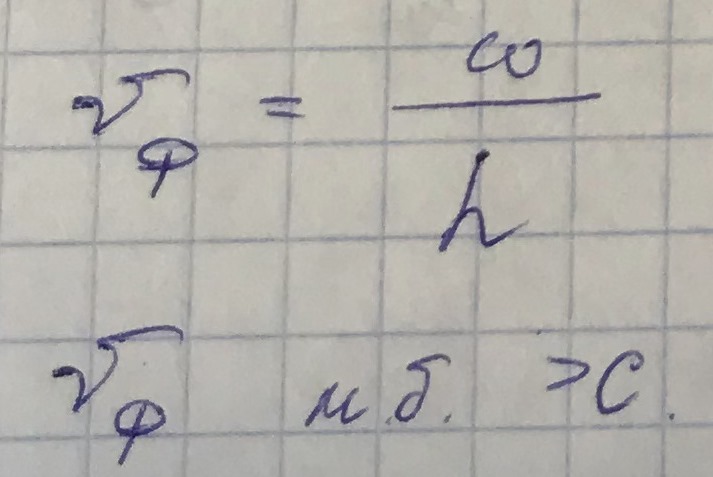
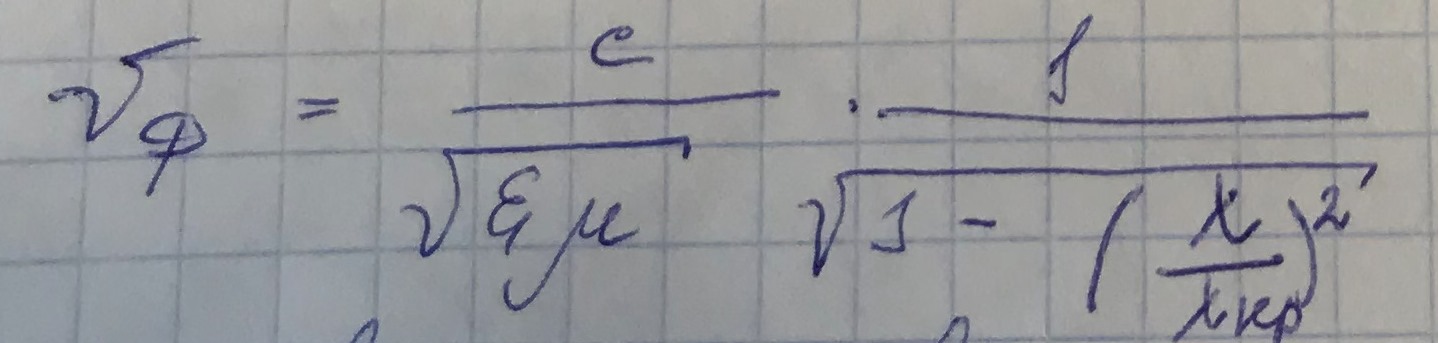
Групповая скорость находится по следующей формуле:
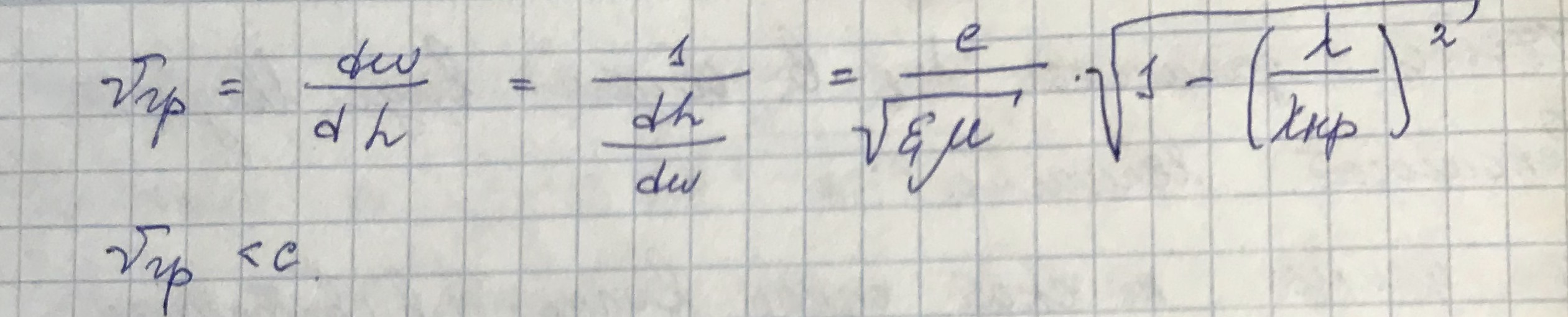
Задания для самостоятельной работы по схеме таксономии Блума.
1. Дайте определение регулярного волновода, опираясь на материал лекции и свои знания.
2. Опишите зависимость волнового числа распространяющейся моды от частоты.
3. Проиллюстрируйте случай, когда фазовая скорость будет больше скорости света.
4. Сравните групповую и фазовую скорости по их значению. В чем суть каждой из них?
5. Подготовьте небольшой рассказ о значении регулярных волноводов в нашей жизни.
6. Произведите оценку своего рассказа на основании критерия верности используемых вами утверждений (опираясь на лекции, другие материалы и ваши личные знания).
>> Пройти тест
>> Посмотреть термины и основные мысли лекции
>> Следующая лекция



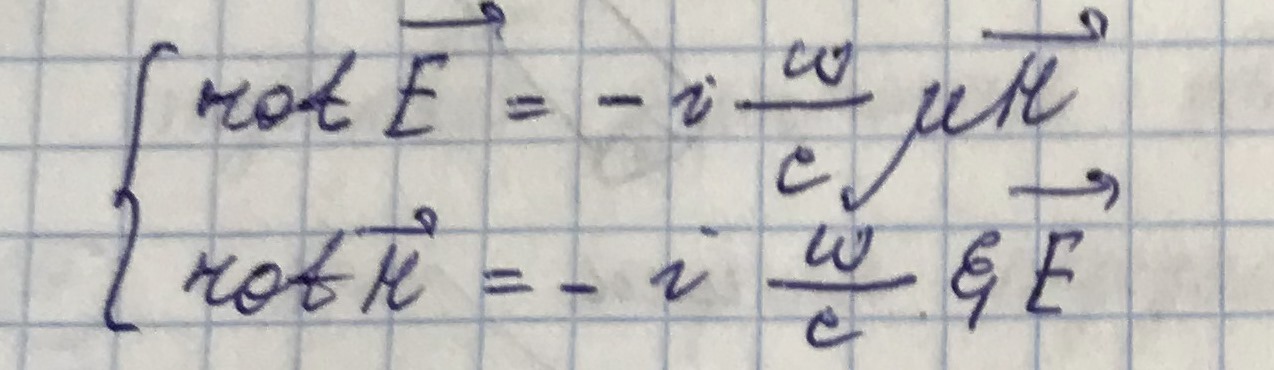
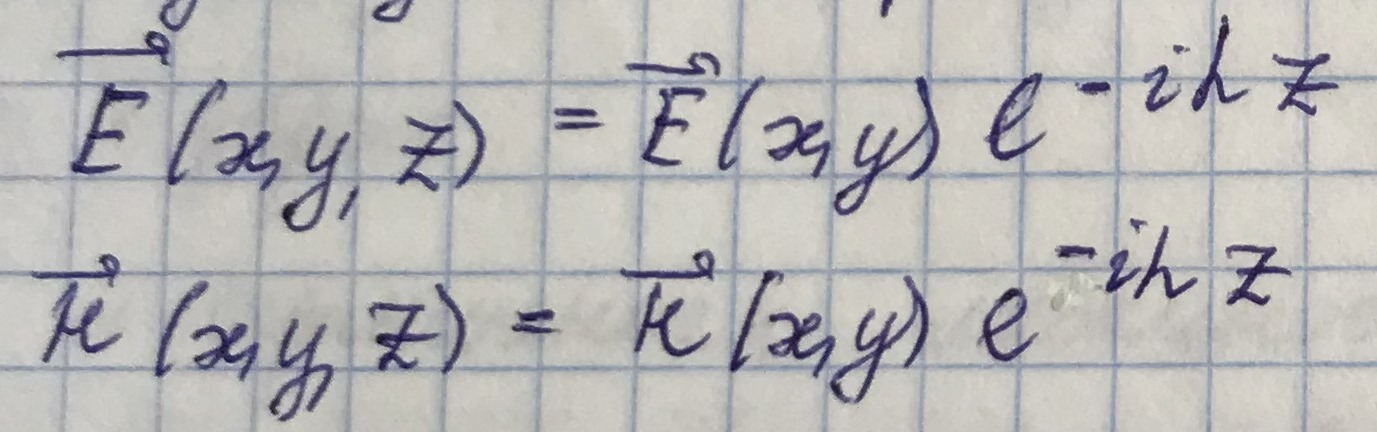
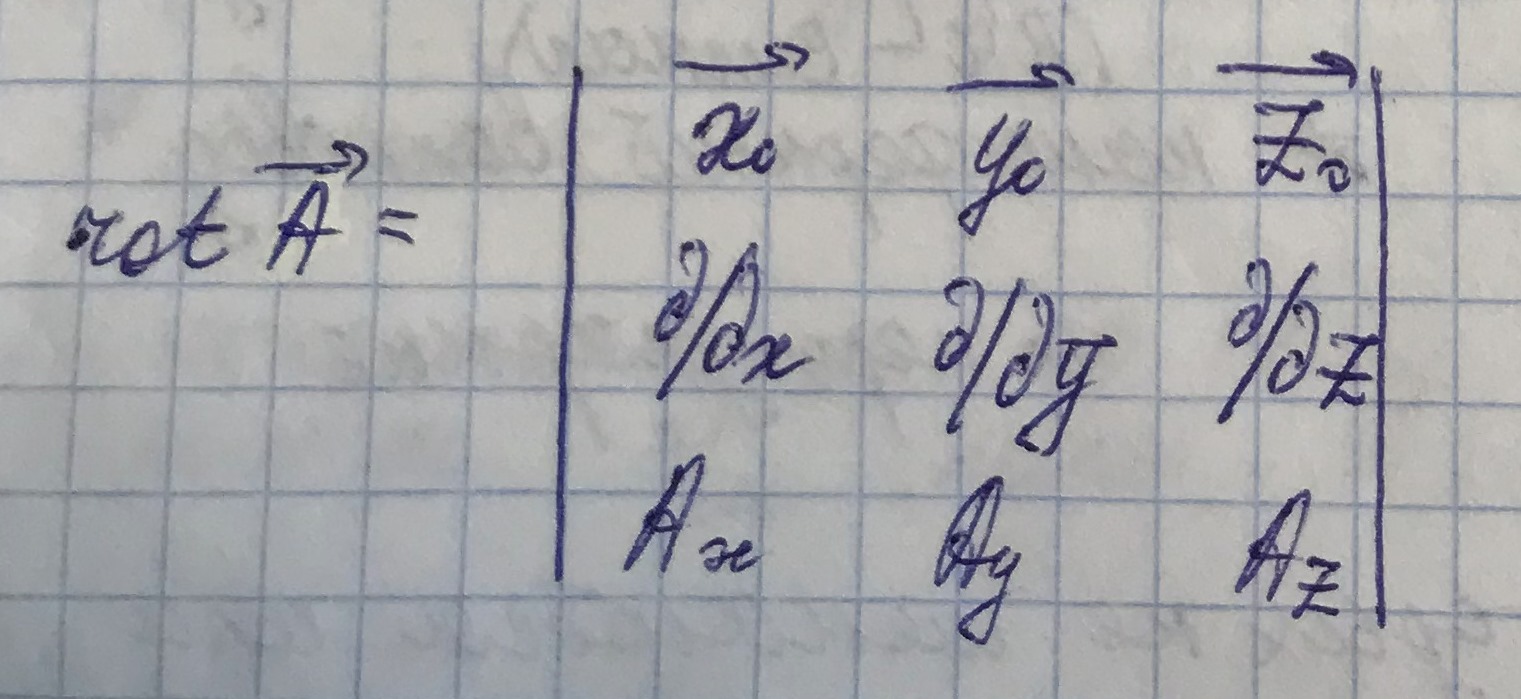

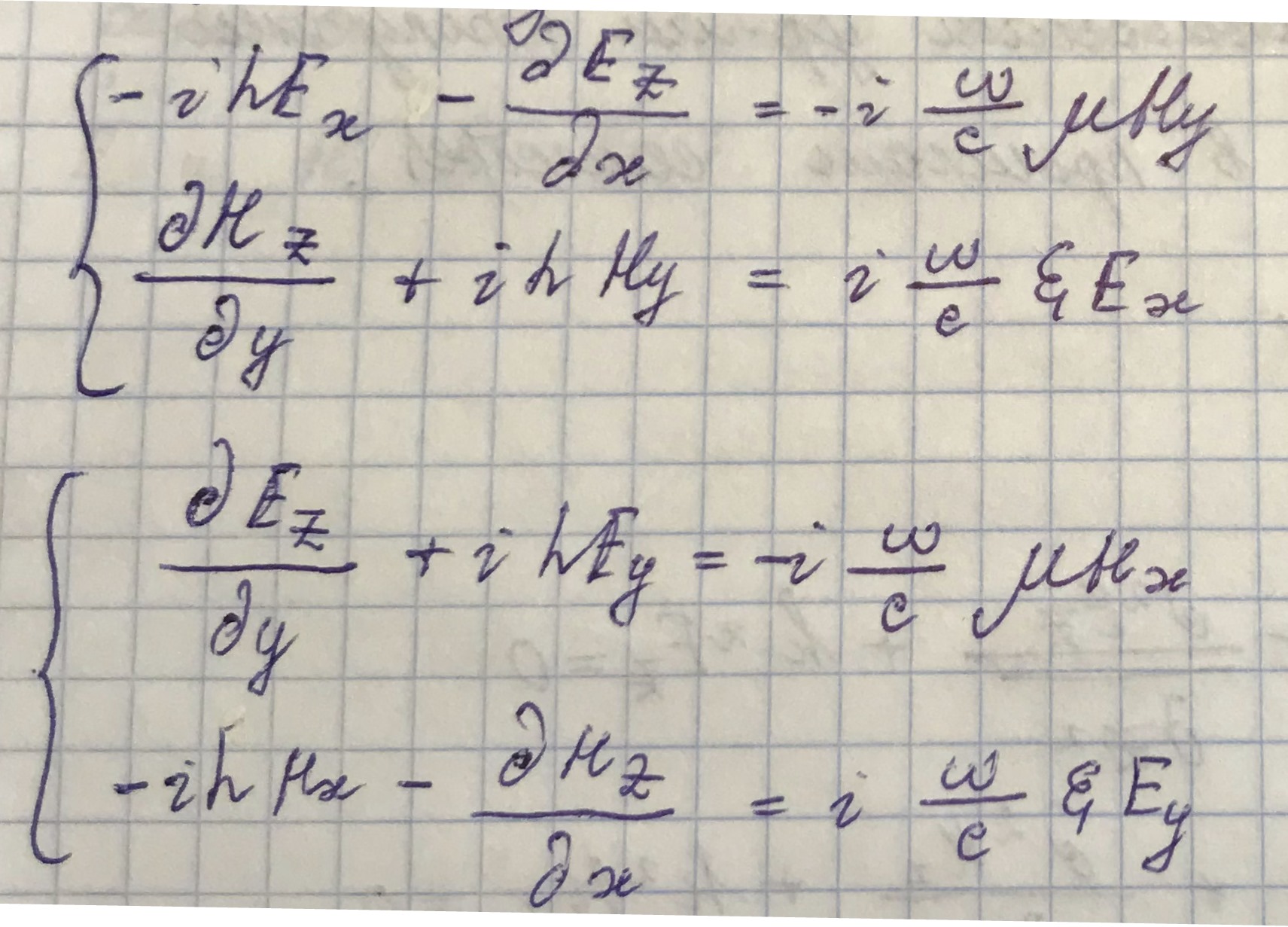
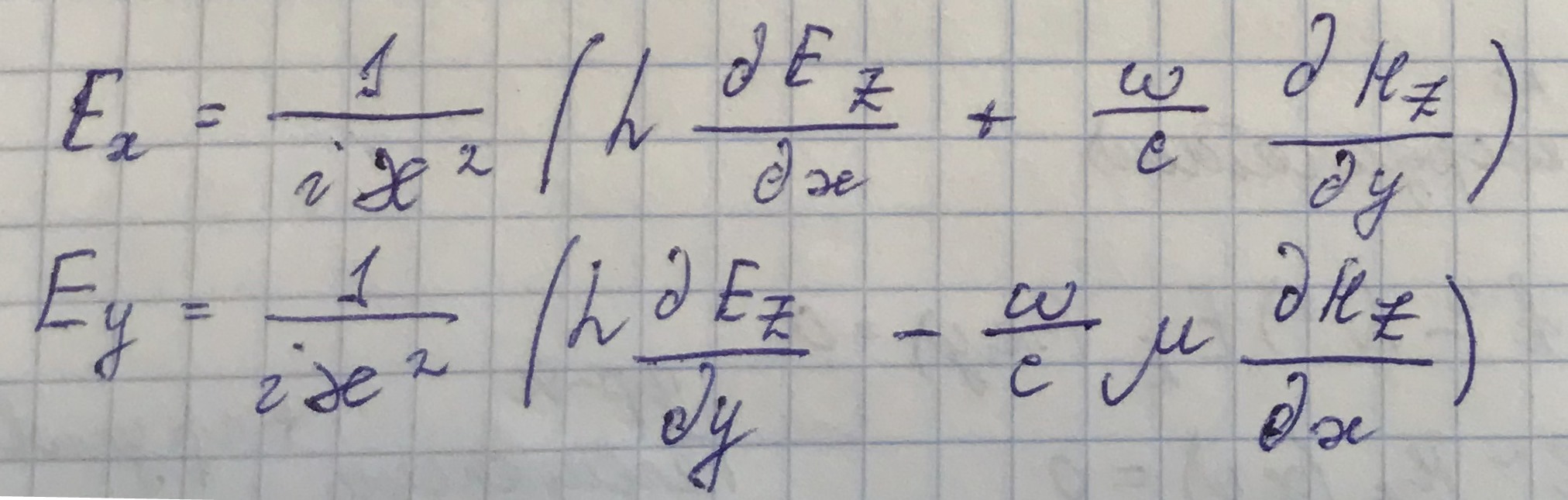
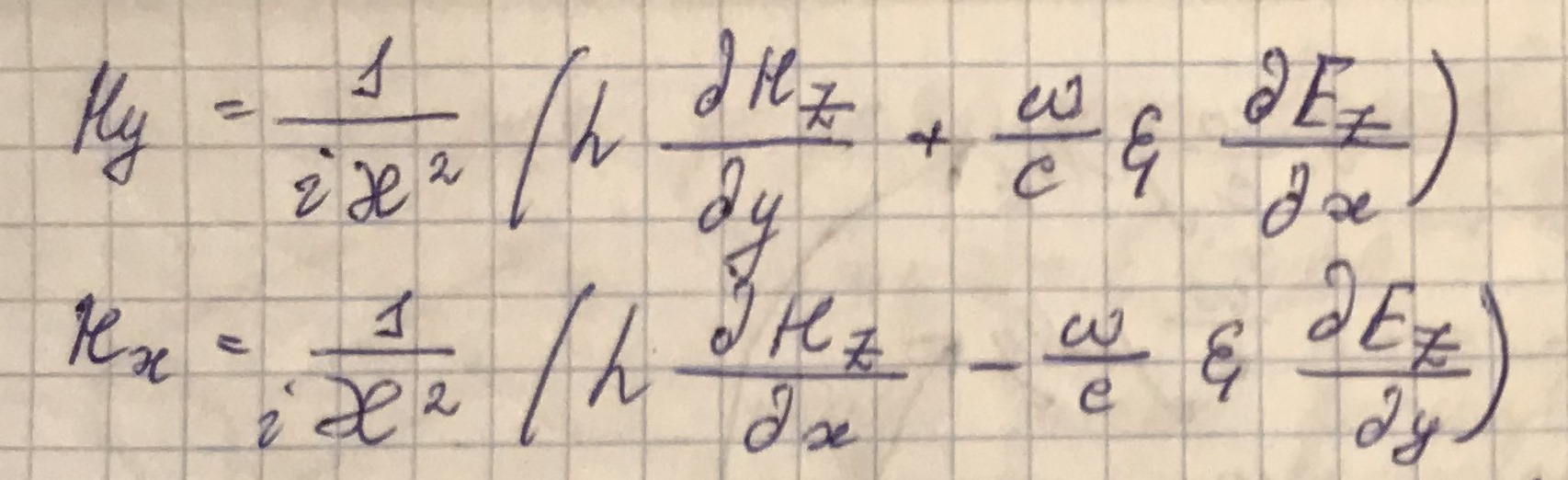
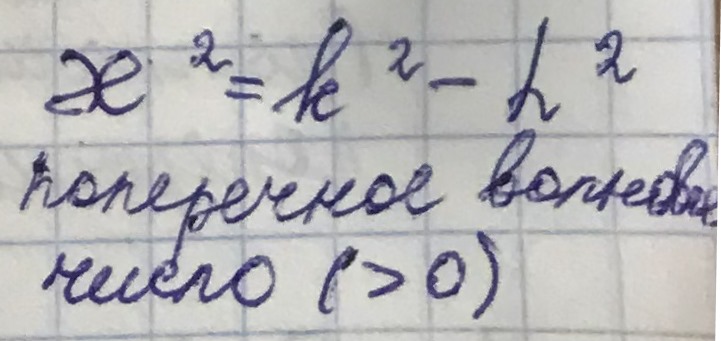
![]() воспользуемся волновыми уравнениями (получены из уравнений Максвелла в прошлом семестре):
воспользуемся волновыми уравнениями (получены из уравнений Максвелла в прошлом семестре):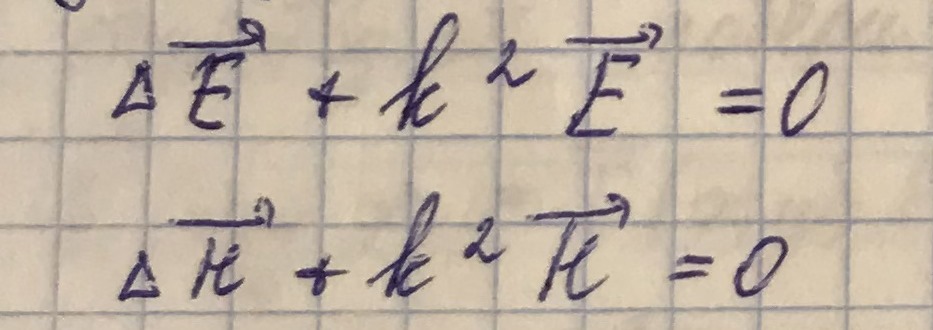

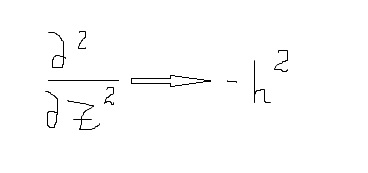 Учитывая это условие, запишем:
Учитывая это условие, запишем: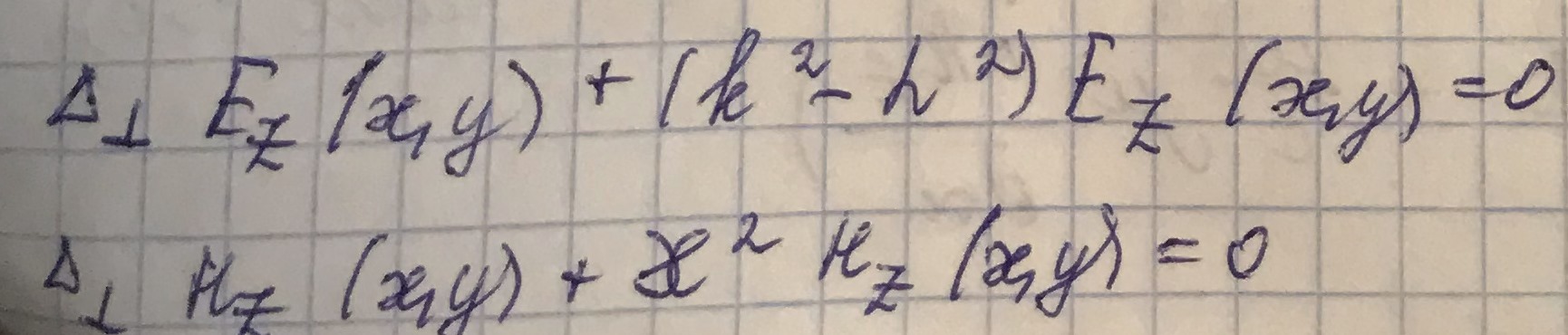
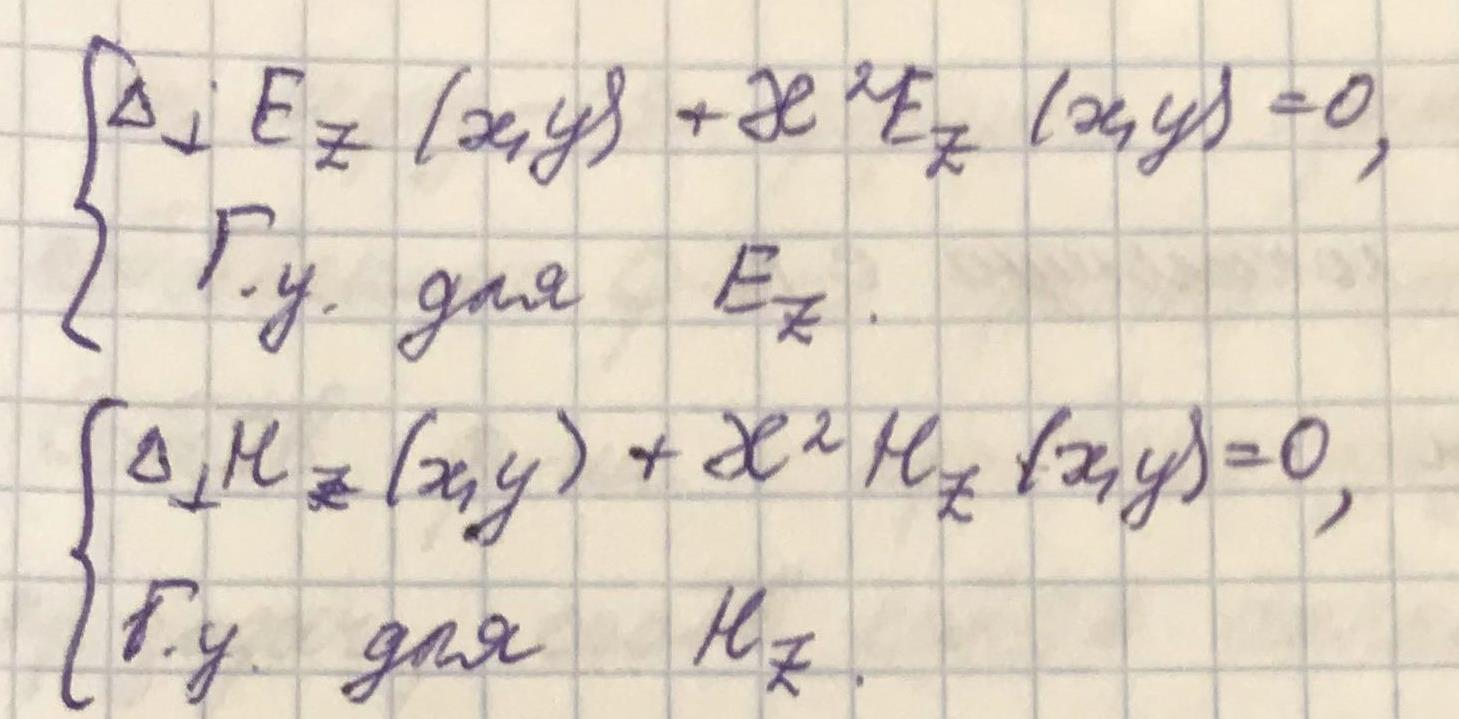
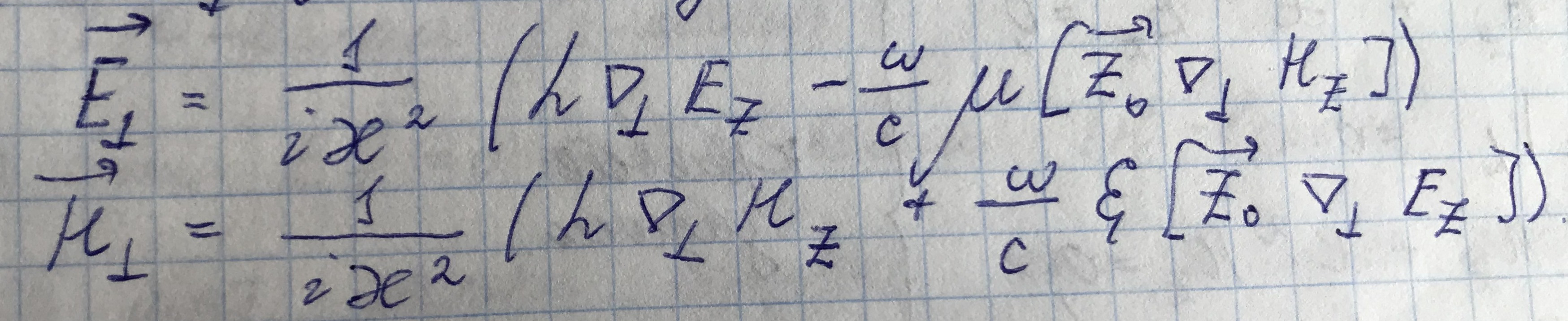
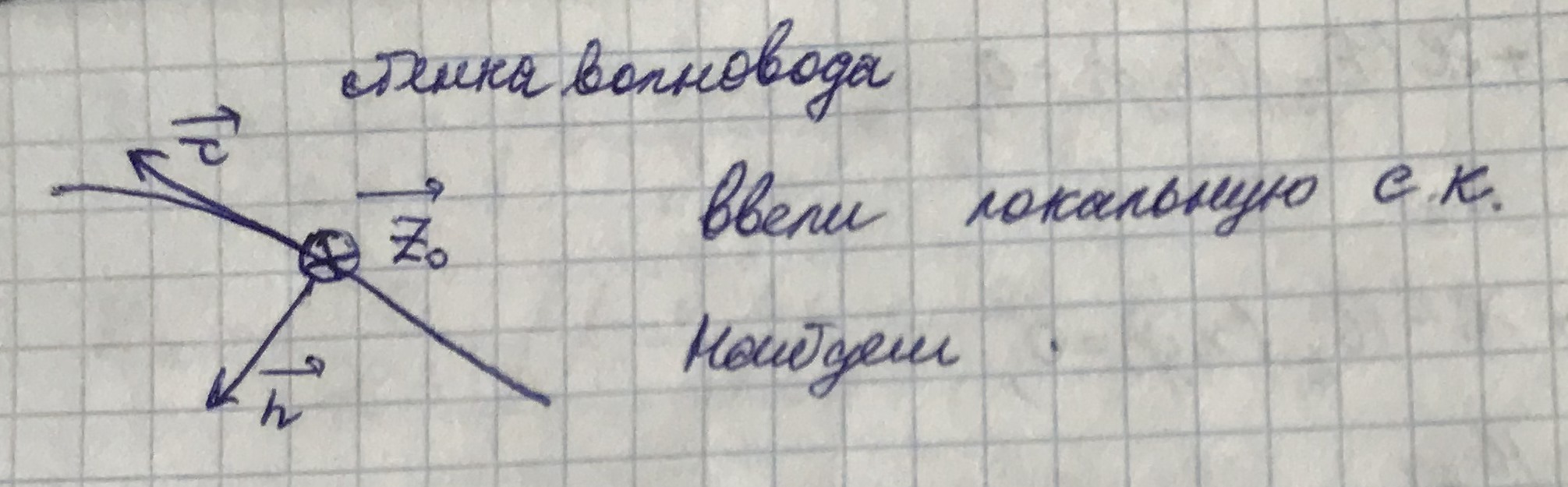
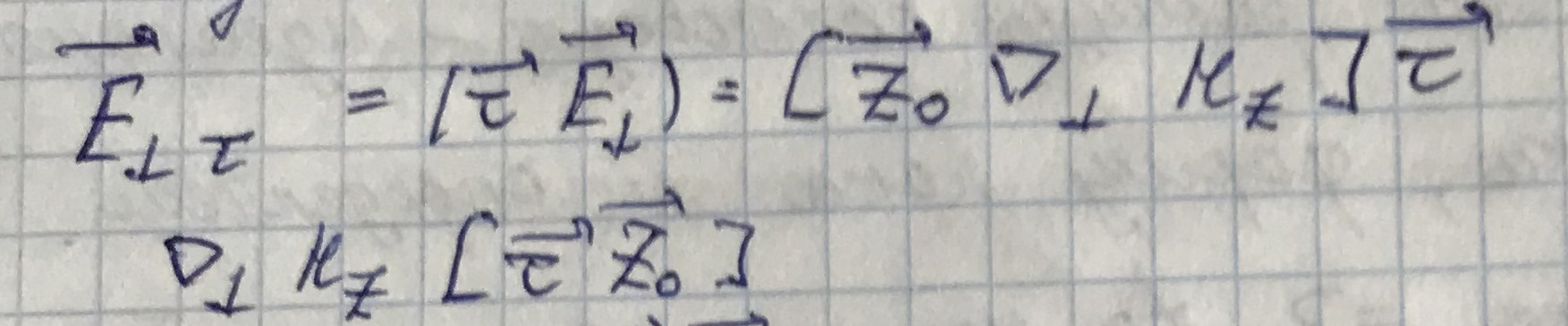
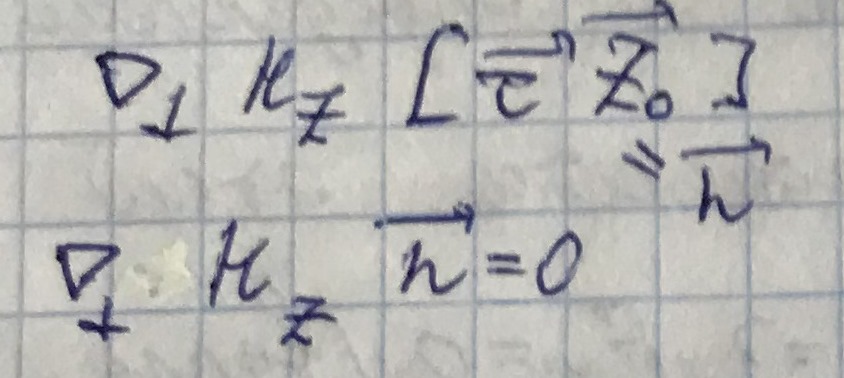 >>
>>