

Решаем задачу на примере коаксиального волновода.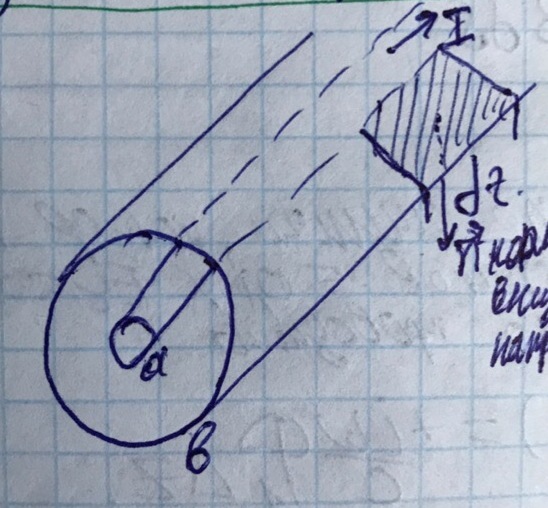
1) Погонная ёмкость
2) Погонная индуктивность

Получили выражения для погонной емкости и погонной индуктивности волновода через его геометрические размеры.
Телеграфные уравнения — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи.
Считаем, что погонные параметры совпадают в статике и для TEM волн.
1. Уравнение для токов.
2. Уравнение для напряжений.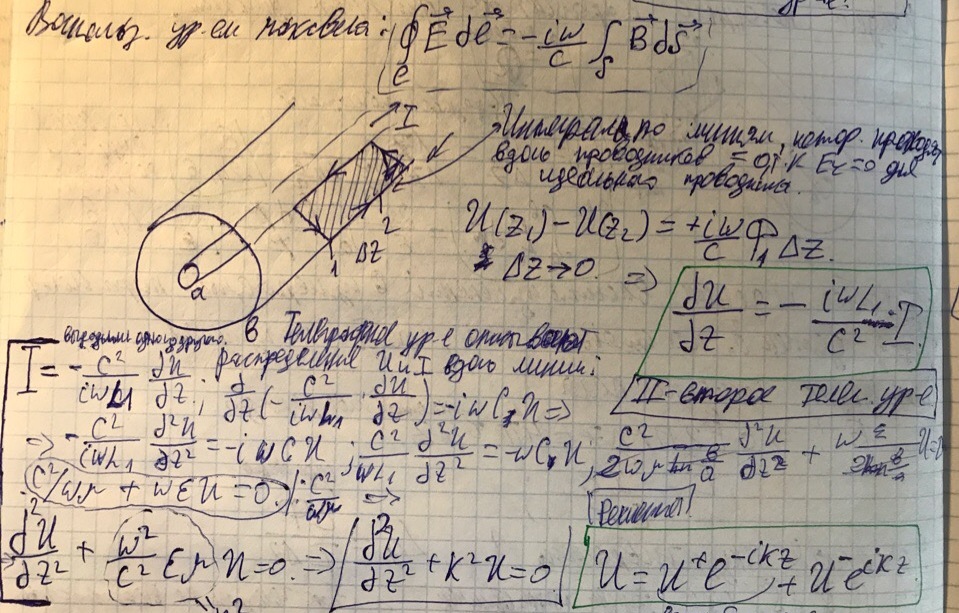
При этом напряжение в данном случае отличается от статического. Введение скалярных величин для токов и напряжений обусловлено удобством в практическом использовании. При этом их значение изменяется только вдоль продольной компоненты z и не зависит от формы траектоии самой линии.
Решение данного уравнения запишем в виде: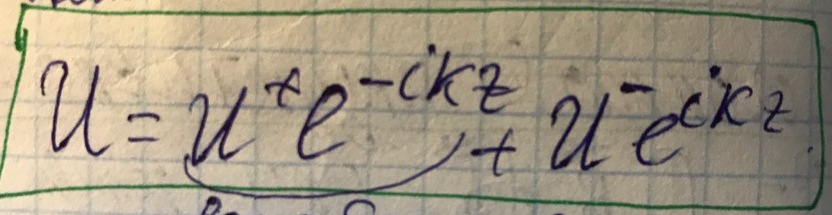
Знак "+" отвечает за компоненту напряжения, направленную вдоль оси z, а знак "-" отвечает за компоненту напряжения, направленную против оси z. Будем работать с волной направленной в положительном направлении z.
Тогда значения напряжения и тока равны:

Рассмотрим коаксиальную линию.
Запишем уравнения для тока и напряжения в ней.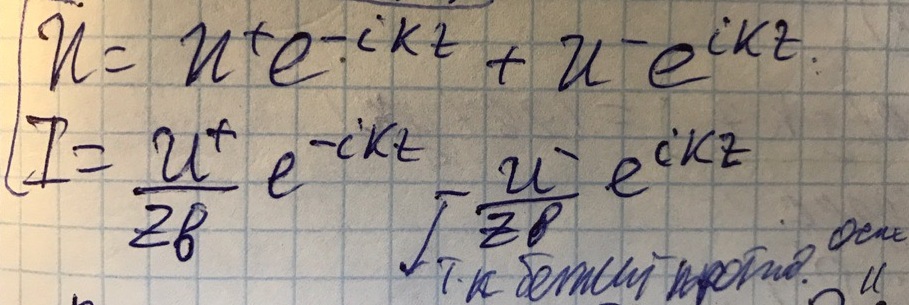
Введем вспомогательную величину, которя называется коэффициентом отражения в сечении z, равное отношению амплитуды отраженной волны, к амплитуде падающей.
Теперь запишем выражение для импеданса в сечении:
Воспользуемся граничным условием, тоесть то, что импеданс в начале координат равен импедансу нагрузки. Из него выразим коэффициент отражения, которе подставим в значение имеданса в сечении:
При этом необходимо преобразовать полученное выражение с помощью формулы Эйлера. После чего получим искомую формулу пересчета импедансов.
|
Термины и понятия (список) |
Главные мысли лекции (5-6 предложений) | Вопросы |
|
Уравнения длинных линий(телеграфные уравнения).
Погонная индуктивность волновода
Погонная емкость волновода Коэффициент отражение. Формула пересчета импедансов. |
1 телеграфное уравнение-уравнение непрерывности: Уравнение для токов. 2 телеграфное уравнение:
уравнение для напряжений Эти уравнение описывают распределение токов и напряжений вдоль линии при заданных C1 L1 Zв определяется конфигурацией проводников. |
Вывод формул: Коэффициент отражения и формулу пересчета импедансов. |
1.Выучите материал лекции.
2. Напишите первое телеграфное уравнение.
3. Что нового вы узнали из этой лекции? Выпишите это.
4. Зачем вводится коэффициент отражения?
5. Самостоятельно выведите формулы.
6. Решите задачу с использованием этих формул.
7. Назовите режимы работы длинной линии.
8. Чему равен коэфициент отражения в режиме холостого хода?
9. Сделайте план-конспект лекции.
10. Систематизируйте полученные знания.
11. Составьте свой тест.