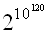Источник: Системные исследования: Ежегодник. – М.: Наука, 1969. С. 30–54.
Интернет-источник

СОДЕРЖАНИЕ

1. Системы повсюду

Каждый, кто захотел бы проанализировать наиболее употребительные современные понятия и ходячие выражения, обнаружил бы в самом начале списка слово «система». Это понятие распространилось во всех сферах науки и проникло в обыденное мышление, в жаргон и в средства массовых коммуникаций. Системное мышление играет ведущую роль в широком диапазоне человеческой деятельности – от индустриального предприятия и средств вооружения до эзотерических тем чистой науки. Системам посвящается несметное множество публикаций, конференций, симпозиумов и учебных курсов. В последние годы появились профессии под такими названиями, как проектирование систем, анализ систем, системотехника и т. д., которые совсем недавно были неизвестны. Они составляют самое ядро новой техники и технократии; специалисты, работающие в этих областях, являются «новыми утопистами» нашего времени (Boguslaw [23]); в отличие от классического поколения утопистов, идеи которых не выходили за пределы книжных полок, они трудятся над созданием Нового Мира, Прекрасного или какого-либо иного.

Этот процесс вызван многими сложными причинами. Одна из них – появление наряду с энергетикой техники автоматического управления. В результате стали развиваться автоматизация, вычислительная техника и т. д. Появились самоуправляющиеся машины – от скромного термостата до самонаводящихся ракет второй мировой войны и значительно усовершенствованных современных моделей ракет. Это привело к изменению «идеологии» исследования. Техника стала рассматриваться в категориях не отдельных изделий, а «систем», включающих в себя не только  разнородные технические процессы – механические, электронные, химические и т. д., но и отношения между человеком и машиной, а также многочисленные финансовые, экономические, социальные и политические проблемы. В результате воздушное или даже автомобильное сообщение не сводится к вопросу о том, сколько машин курсирует по дорогам, а представляет собой систему, которую необходимо планировать и специально создавать. Подобный характер носят многочисленные проблемы, возникающие в современном производстве, коммерции и в процессе создания военной техники.

Все это привело к тому, что «системный подход» стал насущной необходимостью. Если дана некоторая цель, то для того, чтобы найти пути и средства ее реализации, требуется специалист (или группа специалистов) по системам, рассматривающий альтернативные решения и выбирающий те из них, которые обеспечивают оптимизацию, наибольшую эффективность и минимальные затраты в чрезвычайно сложных сетях взаимодействий. Для решения указанных проблем требуются тщательно разработанные технические приемы и совершенные вычислительные машины, значительно превосходящие временные и умственные возможности математика вчерашнего дня. Современные вычислительные машины, автоматизация и кибернетизация и системная наука, вместе взятые, представляют собой развившуюся в последние десятилетия новую техническую революцию, то, что можно назвать «второй промышленной революцией».

Было бы ошибкой относить указанные изменения только к промышленному и военному производству. Ныне даже политические деятели требуют применения «системного подхода», считая его революционно новой концепцией [22; 29], к своим неотложным проблемам, таким, как загрязнение воздуха и воды, перегруженность дорог транспортом, пороки урбанизации, преступность среди молодежи и организованный бандитизм, городское планирование [93] и т. д.

Все эти указанные изменения остались бы только одной из многих граней нынешних изменений в нашем индустриальном обществе, если бы не один существенный момент, который легко упустить, занимаясь детально разработанными и поэтому необходимо ведущими к узкой специализации проблемами вычислительной математики, системотехники и связанных с ними областей знания. Дело заключается не только в технических усовершенствованиях, благодаря которым создаются более крупные и улучшенные изделия (или более прибыльные, обладающие большей разрушающей способностью, или и то и другое вместе). Изменяются основные категории мышления, причем сложность современной техники – только одно и, возможно, не самое важное проявление этого. Так или иначе, но во всех областях современного знания мы вынуждены сталкиваться с необходимостью анализа сложных объектов,  определенных «целостностей» или «систем». Это ведет к фундаментальной переориентации научного мышления.

Мы рассмотрим несколько примеров, выбранных более или менее произвольно, для того чтобы охарактеризовать эту переориентацию.

Начнем с физики. Хорошо известно, что наряду с огромными успехами последних десятилетий в физике возникли также новые проблемы или даже новый тип проблем. Вероятно, неспециалисту прежде всего бросается в глаза факт существования достаточно большого числа – порядка сотни – элементарных частиц, с которыми современная физика не очень-то знает, что делать. По словам одного известного ученого, дальнейшее развитие ядерной физики «требует большой экспериментальной работы, а также создания дополнительных мощных методов оперирования с системами, состоящими из большого, но не бесконечного числа элементов» [31], Эту же мысль выразил в 1964 г. видный физиолог А. Сент-Дьёрди в довольно причудливой форме: «Когда я приступил к работе в Институте перспективных исследований в Принстоне, я надеялся, что в компании великих атомных физиков и математиков я смогу кое-что узнать о живой материи. Но когда я однажды обмолвился о том, что в любой живой системе имеется больше двух электронов, физики не захотели говорить со мной. Со всеми своими вычислительными машинами они не в состоянии были сказать, что мог бы делать третий электрон. Замечательно, что сам этот электрон хорошо знает, что ему делать. Таким образом, маленький электрон знает нечто такое, чего не знают все мудрые мужи Принстона, причем то, что он знает, должно быть чем-то очень простым» [85].

Триумф молекулярной биологии в последние годы, значительные успехи в исследовании генетического кода, новые достижения генетики, эволюционной теории, медицины, физиологии клеток и многих других областей биологии хорошо известны. В ходе этого развития становится все более явной необходимость построения «организмической» биологии, о чем автор настоящей статьи говорил на протяжении почти сорока последних лет. Биология должна интересоваться не только физико-химическим или молекулярным уровнями, но и более высокими уровнями организации живого. Это требование выдвигается с новой силой в условиях современного развития биологических знаний, однако едва ли добавился хотя бы один новый аргумент по сравнению с тем, что мы обсуждали ранее (см. Берталанфи [10; 11; 14]).

Если мы далее обратимся к психологии, то здесь долгое время в качестве основной концепции использовалась «модель робота». Поведение при этом объяснялось при помощи механистической схемы «стимул – реакция» (S – R); по образцу экспериментов над животными обусловливание выступало как основа человеческого поведения, что приводило к отрицанию его специфики и т. д. Гештальт-психология почти 50 лет назад первой выступила против механистической схемы. Позже было предложено много попыток более удовлетворительно объяснить «образ человека», причем большинство из них базировалось на понятии системы [19]. Согласно Э. Хану, Пиаже, например, «определенно связывает свою концепцию с общей теорией систем Берталанфи» [41]. В психиатрии системная точка зрения принята, возможно, даже в большей мере, чем в психологии (см., например, [59; 18; 40; 39]).

Аналогичное положение и в социальных науках. Путаница и противоречия, характерные для широкого спектра современных социологических теорий (Sorokin [82; 83]), заставляют сделать одно твердое заключение: социальные явления должны рассматриваться как «системы».

Течение событий в наше время побуждает к принятию подобной концепции и в истории, учитывая, что в конечном счете история есть социология, взятая применительно к процессу развития рассматриваемых явлений: одни и те же социокультурные сущности в социологии исследуются в их нынешнем состоянии, а в истории – в процессе их становления.

В то время как социология (и, вероятно, история) имеет дело с неформальными организациями, другое современное направление исследований разрабатывает теорию формальных организаций, т. е. таких, которые создаются планомерно, например структура армии, бюрократии, делового предприятия и т. д. Это направление также «базируется на философии, принимающей в качестве предпосылки, что единственным осмысленным путем изучения организации является изучение ее как системы»; системный анализ рассматривает «организацию как систему взаимосвязанных переменных»; поэтому «современная теория организации неразрывно связана с проблематикой общей теории систем» (Scott [77]). Приведем слова Р. Акофа – видного специалиста в области исследования операций: «В последние два десятилетия мы являемся свидетелями быстрого развития понятия «система», ставшего ключевым в научном исследовании. Конечно, системы изучались в течение многих столетий, но теперь в такое исследование добавлено нечто новое... Тенденция исследовать системы как нечто целое, а не как конгломерат частей соответствует тенденции современной науки не изолировать исследуемые явления в узкоограниченном контексте, а изучать прежде всего взаимодействия и исследовать все больше и больше различных аспектов природы. Мы уже наблюдали, как под флагом системного исследования (и многих его синонимов) осуществлялась конвергенция многих весьма специальных современных научных движений... Эта и многие другие подобные формы научного исследования представляют собой коллективную деятельность, включающую постоянно расширяющийся спектр научных и технических дисциплин. Мы участвуем в том, что, вероятно, является наиболее широкой из предпринятых до сих пор попыток достигнуть синтеза научного знания» [1]. 

Таким образом, круг замкнулся, и мы вновь вернулись к тем направлениям развития современного индустриального общества, с которых начали наше рассмотрение. Каким бы отрывочным и поверхностным ни был наш анализ, из него следует, что для современных наук и современной жизни необходимы существенно новые понятия, новые идеи и категории, которые так или иначе концентрируются вокруг понятия «система». В этой связи приведем мнение советского автора: «Разработка специфических методов изучения системных объектов является одной из черт современного научного знания, тогда как для науки XIX века было характерно преимущественное внимание к выделению "элементарных" образований и процессов в природе» (Ю. А. Левада [55] – цит. по [41]).

Мы должны также упомянуть очевидные опасности этого нового направления научного исследования. По словам психотерапевта Рюша, новый кибернетический мир интересуется не людьми, а «системами» [75]. По выражению Богуслава [23], для новых утопистов, исповедующих идеи системотехники, «человеческий элемент» является наиболее ненадежным звеном. Или он должен быть изъят и заменен материальными сооружениями – вычислительной техникой, саморегулирующимися машинами и тому подобным, или же его необходимо сделать надежным, насколько это возможно, т. е. машиноподобным, конформистским, управляемым и стандартизированным. Говоря более резко, человек в Большой системе должен быть – и в значительной степени уже стал – умственно недоразвитым нажимателем кнопок или обученным идиотом, т. е. высококвалифицированным в своей специальности, но во всех других отношениях представляющим собой лишь часть машины. В соответствии с хорошо известным системным принципом – принципом прогрессирующей механизации – индивид во все большей степени становится зубчатым колесом некоторой сложной конструкции, управляемой несколькими привилегированными лидерами, которые за дымовой завесой идеологий преследуют свои частные интересы [83, стр. 588 и след.].

Вне зависимости от того, какие специальные цели мы преследуем – то ли анализ позитивного влияния теории систем на развитие научного знания и увеличение возможности управления окружающей средой и обществом, то ли мы видим в системном движении появление некоего «Прекрасного Нового Мира», – в обоих случаях необходимо интенсивное изучение этого движения.

2. История теории систем

Насколько мы можем судить, концепция «общей теории систем» впервые была предложена автором настоящей работы еще до появления кибернетики, системотехники и связанных с ними дисциплин. Конечно, как и любое другое научное понятие, понятие системы имеет свою долгую историю. Хотя сам термин «система» далеко  не всегда явно выделялся, эта история богата именами многих философов и ученых. В этой связи необходимо упомянуть «натуральную философию» Лейбница, Николая Кузанского с его совпадением противоположностей, мистическую медицину Парацельса, предложенную Вико и Ибн-Халдуном версию истории последовательности культурных сущностей, или «систем», диалектику Маркса и Гегеля, – этот перечень, конечно, далеко не полон. Литературный гурман может также вспомнить «De ludo globi» («Об игре, то есть вращении земного шара») Николая Кузанского (см., в частности [9]) и «Glasperlenspiel» («Игра стеклянных бус») Германа Гессе – в обоих случаях преобразование мира понимается как искусно задуманная абстрактная игра.

Нескольких ученых можно считать непосредственными предшественниками общей теории систем. В. Кёлер [51], выдвинувший проблему «физических гешталътов», шел в этом направлении, но поставил проблему систем во всем объеме, ограничивая ее рассмотрением гештальтов в физике (и возможностью интерпретировать на этой основе биологические и психологические явления). В своей более поздней публикации 1927 г. [52] Кёлер выдвинул тезис о теории систем, предполагающий изучение общих свойств неорганических систем в сравнении с органическими; до некоторой степени это требование было выполнено в теории открытых систем. А. Лотка в своей классической работе 1925 г. [57] ближе всего подошел к этой цели, и основными формулировками на этот счет мы обязаны ему. Он действительно рассматривал общее понятие системы (не ограничивая его, как Кёлер, физическими системами). Лотка, однако, был статистиком, и его более интересовали проблемы популяции, чем биологические проблемы отдельного организма. Этим можно объяснить некоторые непоследовательности в концепции Лотки: он, например, рассматривал сообщества как системы и в то же время считал отдельный организм суммой клеток.

Несмотря на блестящую плеяду предшественников общей теории систем, осознание необходимости и возможности системного подхода произошло только в самое последнее время. Его необходимость является следствием того, что была доказана недостаточность механистической схемы изолированных причинных цепей и меристских концепций, особенно для биологических наук и практических проблем, поставленных современной техникой. Его возможность является следствием многообразных новых исследований – теоретических, эпистемологических, математических и т. д., которые, хотя ныне они только начаты, делают системный подход все более осуществимым.

В начале 20-х годов автора настоящей статьи стали приводить в недоумение очевидные пробелы в биологических – эмпирических и теоретических исследованиях. Уже упоминавшийся механистический подход, господствовавший в то время, казалось, не замечал или активно отрицал как раз то, что существенно в явлениях жизни.  Автор защищал организмическую концепцию в биологии, подчеркивающую необходимость рассмотрения организма как целого или системы и видящую главную цель биологических наук в открытии принципов организации живого на его различных уровнях. Первые наши работы на этот счет восходят к 1925–1926 гг. Отметим, что именно в это время была опубликована философия «органического механизма»Уайтхеда (1925 г.) [91]. Несколько позже появились работы Кэннона по гомеостазису (в 1929 и 1932 гг.) [27; 28]. Великим предшественником организмической концепции был Клод Бернар, но за пределами Франции его труды были малоизвестны; даже теперь они еще не вполне оценены [8; стр. 960]. Одновременное появление сходных идей независимо друг от друга и на разных континентах было симптомом возникновения новой обобщенной научной концепции; потребовалось, однако, некоторое время для того, чтобы она приобрела популярность,

Здесь мы должны сделать маленькое замечание личного порядка. В последние годы ведущие американские биологи (Dubos [33; 34]; Dobzhansky [32]; Commoner [30]) вновь подчеркивают значение «организмической биологии», не упоминая, однако, ранних работ автора на этот счет, хотя в литературе Европы и, в частности, у ряда ученых социалистических стран (например, Ungerer [88]; Blandino [21]; Tribino [87]; Канаев [50]; Kamaryt [48; 49]; Bendmann [6; 7]; Афанасьев [2]) они получили должное признание.

Философское образование автор получил в духе традиций неопозитивизма группы Морица Шлика, которая позже стала известна как Венский кружок. Несомненно, однако, что интерес к немецкому мистицизму, историческому релятивизму О. Шпенглера, истории современного искусства и другим подобным неортодоксальным направлениям помешал мне стать добропорядочным позитивистом. Более сильными были мои связи с Берлинской группой 20-х годов – «Обществом эмпирической философии», в котором видную роль играли философ-физик Ганс Рейхенбах, психолог А. Герцберг, инженер Парсеваль и др.

В связи с экспериментальной работой по метаболизму и росту, с одной стороны, и попытками конкретизировать организмическую программу – с другой, мною была предложена в 30-е годы программа теории открытых систем, основанная скорее на том тривиальном факте, что организм представляет собой открытую систему, нежели на какой-либо развернутой биологической теории, существовавшей в то время. На этой базе возникла необходимость распространить традиционную физическую теорию на биофизику путем обобщения кинетических принципов и термодинамической теории; в рамках последней была разработана термодинамика необратимых процессов.

Впоследствии оказалось возможным дальнейшее обобщение. Выяснилось, что ко многим явлениям биологии, а также явлениям бихевиоральных и социальных наук применимы определенные математические понятия и модели, которые неприложимы к объектам, исследуемым в физике и химии, и в этом смысле превосходят физику как образец «точной науки». Стало также очевидным структурное подобие, изоморфизм таких моделей, построенных для различных областей; при этом в центре внимания оказались проблемы порядка, организации, целостности, телеологии и т. д., которые демонстративно исключались из рассмотрения в механистической науке. Такова в общих чертах исходная идея «общей теории систем».

Надо сказать, что существовавшая в этот период ситуация не благоприятствовала развитию такой концепции. В то время было принято отождествлять биологию с лабораторным, чисто экспериментальным исследованием, и автор уже перешел все границы дозволенного, когда он в 1932 г. опубликовал книгу «Theoretische Biologie» («Теоретическая биология») [11], посвященную несколько иной области биологии, только недавно обретшей академическую респектабельность. В наши дни, когда существует ряд журналов, публикующих многочисленные статьи по общей теории систем, и когда построение моделей превратилось в модное и весьма почетное занятие, даже трудно себе вообразить возможность сопро-тивления этим идеям. Однако это было так. Одобрение общей теории систем со стороны покойного профессора Отто Пётцля, хорошо известного венского психиатра, помогло преодолеть некоторые трудности и подготовить публикацию, вводящую в ее проблематику. И опять вмешалась судьба. Написанная с этой целью статья для «Deutsche Zeitschrift fur Philosophic» достигла стадии корректуры, но номер журнала был уничтожен в годы войны. После войны принципы общей теории систем неоднократно излагались нами в лекциях, широко обсуждались с физиками [12] и дискутировались на специальных симпозиумах [20].

С момента своего возникновения теория систем сразу же натолкнулась на критику, которая видела в ней фантастическую и весьма самонадеянную концепцию. Некоторые утверждали, что общая теория систем тривиальна, поскольку так называемые изоморфизмы суть лишь трюизмы, говорящие, что математику можно применять к любым вещам, и поэтому теория систем имеет значение, не большее, чем «открытие», что 2 + 2 = 4 одинаково справедливо и для яблок, и для долларов, и для галактик. Другие считали ее ошибочной из-за поверхностных аналогий вроде известного сравнения общества с «организмом», которое скрывает действительные различия и в силу этого приводит к неверным и даже морально нежелательным выводам. Или же, наконец, ее признавали философски и методологически необоснованной из-за пресловутой «несводимости» более высоких уровней к более низким, то есть на основе тенденции отрицания роли аналитического исследования, успехи которого в таких областях, как сведение  химии к физическим принципам или жизненных явлений к молекулярной биологии, в настоящее время совершенно очевидны.

Постепенно, однако, начали осознавать, что такие возражения упускают из виду то, для чего, собственно, была выдвинута теория систем, а именно задачу построения научного объяснения и теоретического знания в тех областях науки, где прежде их не было, и достижения более высокой степени обобщения, чем это позволяют сделать специальные науки. Эта ситуация удачно подытоживается в письме экономиста К. Боулдинга, которое он направил автору данной статьи в 1953 г.: «Я, кажется, получил выводы, которые во многом сходны с Вашими, хотя пришел к ним от экономики и социальных наук, а не от биологии: существует некоторая основа – я назвал ее «общей эмпирической теорией», Вы очень удачно – «общей теорией систем» – которая широко применима во многих различных дисциплинах. Я уверен, что многие люди во всем мире подошли по существу к той же позиции, что и мы, но все мы рассеяны и не знаем друг друга, так как очень трудно пересечь границы отдельных научных дисциплин».

В первый год работы Центра по развитию исследований в бихевиоральных науках (Пало Альто) произошла встреча К. Боулдинга, биоматематика А. Рапопорта, физиолога Ральфа Жерара и автора этих строк; на ежегодном конгрессе 1954 г. Американской ассоциации развития науки (American Association for the Advancement of Science – AAAS) нам удалось реализовать проект создания «Общества общей теории систем» («Society for General System Theory»). Это название позже было изменено на менее обязывающее – «Общество исследований в области общей теории систем» («Society for General Systems Research»); это Общество входит в качестве филиала в AAAS, а его собрания, привлекающие большое число участников, стали неотъемлемой частью съездов AAAS. Местные группы Общества организованы в различных центрах США, и по их примеру созданы рабочие группы в Европе. Первоначальная программа Общества не нуждается в пересмотре: «Общество исследований в области общей теории систем» организовано в 1954 г. в целях содействия развитию теоретического анализа систем, результаты которого могут применяться более чем к одному из традиционных разделов научного знания. Его главные функции таковы: 1) исследование изоморфизмов понятий, законов и моделей в различных областях науки для их переноса из одной дисциплины в другую; 2) способствование построению адекватных теоретических моделей для тех областей науки, в которых они отсутствуют; 3) минимизация дублирования теоретических исследований в различных научных областях; 4) содействие выявлению единства науки путем установления связей между специалистами различных наук».

Общество начиная с 1956 г. издает ежегодник «General Systems» под редакцией А. Рапопорта и Л. фон Берталанфи. Редакция  «General Systems» намеренно не проводит строгой политики отбора статей, а предоставляет место для статей различных направлений, как, вероятно, и надлежит делать в области, испытывающей острую потребность в новых обобщающих идеях и исследованиях. Как правило, ведущиеся разработки и публикации посвящаются применению принципов общей теории систем к специальным научным дисциплинам; эта тенденция нашла свое выражение, в частности, в создании в самое недавнее время журнала «Mathematical Systems Theory» («Математическая теория систем»).

Тем временем развивалось и другое современное направление научного исследования. В 1948 г. вышла в свет «Кибернетика» Норберта Винера, которая обобщила и подвела итоги научных достижений того времени в вычислительной технике, теории информации и теории саморегулирующихся устройств. Тот факт, что три фундаментальных исследования – «Кибернетика» Н. Винера (1948) [92], теория информации К. Шеннона и У. Уивера (1949) [78] и теория игр Дж. фон Неймана и О. Моргенштерна (1944) [63] – появились почти одновременно, представлял собой, конечно, одно из совпадений, которые случаются, однако, лишь тогда, когда идеи витают в воздухе. Винеровские кибернетические понятия, в частности понятия обратной связи и информации, далеко выходят за пределы техники; они приложимы к явлениям биологии и социологии. Нельзя сказать, что кибернетика возникла на пустом месте. Одним из ее краеугольных камней было кэнноновское понятие гомеостазиса. Менее широко известно, что детальные модели обратной связи для физиологических явлений были разработаны немецким физиологом Рихардом Вагнером в 20-х годах [89], швейцарцем, нобелевским лауреатом В. Р. Гессом [44; 45] и Эрнстом фон Хольстом в работе «Reafferenzprinzip» («Принцип обратной афферентации»). Однако своей огромной популярностью в науке, технике и общественном мнении кибернетика обязана, конечно, Винеру и провозглашенной им идее о второй промышленной революции.

Тесная связь кибернетики и системных исследований хорошо показана в программном заявлении Л. Франка на открытии конференции по кибернетике в 1948 г.: «На протяжении долгого времени понятия целенаправленного поведения и телеологии ассоциировались с таинственной способностью к с самосовершенствованию, или достижению цели, или с конечной причиной, обычно сверхчеловеческого или сверхъестественного происхождения. Для того чтобы продвинуться в изучении явлений, научное мышление должно было отвергнуть такую веру в цель и все телеологические понятия ради строго механистического и детерминистского взгляда на природу. Эта механистическая концепция прочно укрепилась после того, как было доказано, что в основе Вселенной лежит действие безликих частиц, движущихся наугад, беспорядочным образом. Ввиду множественности этих частиц возникают порядок и регулярность статистического характера… Неоспоримый успех этих понятий и методов в физике и астрономии, а позже и в химии, задал линию развития для биологии и физиологии. Этот подход к проблемам живых организмов был усилен аналитической предрасположенностью западноевропейской культуры и спецификой используемых нами языков. Наши исследовательские традиции и наши научные языки со строгими значениями их терминов побуждают нас подходить ко всему, что мы изучаем, как к составленному из отдельных дискретных частей или факторов, которые мы должны попытаться изолировать и рассматривать как потенциальные причины. Иначе говоря, в этом случае мы имеем дело с проблемами анализа отношения двух переменных. Сегодня мы являемся свидетелями поисков новых научных подходов, новых и более многогранных понятий и методов, позволяющих рассматривать организм и личность как целое. Понятие телеологического механизма, в каких бы различных терминах оно ни выражалось, представляет собой попытку избавиться от этих устаревших формулировок, которые теперь нам кажутся неадекватными, и создать новые и более плодотворные концепции и более эффективную методологию для изучения саморегулирующихся процессов, самоориентирующихся систем и организмов и самонаправляющихся личностей. Таким образом, термины "обратная связь", "сервомеханизм", "круговая система", "круговой процесс" следует рассматривать как различные, но эквивалентные выражения одной и той же основной концепции» [37].

В заключение настоящего раздела статьи мы хотим обратить внимание на ряд получивших хождение ошибочных формулировок и неверных интерпретаций. Так, Бакли (Buckley [26; стр. 36]) утверждает, что «современную теорию систем, хотя она и выглядит как появившаяся de novo из достижений последней войны, можно считать кульминационным пунктом широкого сдвига в научной перспективе, происходящего в последние столетия». Вторая часть этой фразы справедлива, первая – нет; теория систем не «появилась из достижений последней войны», а уходит своими корнями, как мы уже писали об этом, глубоко в историю, и причины, приведшие к ее созданию, определяются не производством средств вооружения и связанным с ним развитием техники. Ошибочно также считать, что «теория систем появилась из последних достижений в исследовании технических систем» (Shaw [79]), исключая некоторый частный смысл этого утверждения.

Теория систем часто отождествляется с кибернетикой и теорией управления. Это опять-таки неверно. Кибернетика как теория механизмов управления в технике и природе, основанная на понятиях информации и обратной связи, есть только часть общей теории систем; кибернетические системы – частный, хотя и важный случай систем. 

3. Различные направления в разработке теории систем

В наше время, когда любое новшество, каким бы тривиальным оно ни было, провозглашается как новая «революция», нужно с большой осторожностью использовать этот термин для характеристики тех или иных научных направлений. Понятие «научная революция» можно осознанно применять лишь в том случае, если дать ему строгое операциональное определение.

Т. Кун в своей книге «Структура научных революций» [54] специфику научных революций видит в появлении новых концептуальных схем, или парадигм. Такие парадигмы выдвигают на передний план те аспекты науки, которые ранее не замечались, или не осознавались, или даже подавлялись «нормальной» наукой, т. е. наукой, общепринятой и практикуемой в данное время. Следовательно, в периоды научных революций происходят сдвиги в исследуемых проблемах и изменение правил научной деятельности, которые можно сравнить со сдвигами в воспринимаемых гештальтах в известных психологических экспериментах, когда, например, вместо чашки видят два профиля или вместо кролика – утку. Понятно, что в такие критические периоды особое значение приобретает философский анализ, необходимость которого не осознается в периоды роста «нормальной» науки. Ранние версии новой парадигмы в большинстве случаев являются незрелыми, позволяют решать очень немногие проблемы, причем решения, даваемые в этот период отдельным проблемам, далеки от совершенства. Новая парадигма реализуется, как правило, в существовании большого числа различных теорий и конкуренции между ними, при этом каждая теория ограничена как в отношении охватываемых ею проблем, так и создаваемых ею изящных решений. Но во всех случаях новая парадигма действительно охватывает новые проблемы, особенно те, которые раньше отвергались как «метафизические».

Эти критерии получены Куном на основе изучения «классических» революций в физике и химии, но они представляют превосходное описание изменений, вызванных происходящим в последнее время введением в науку организмических и системных понятий, и проливают свет на их достоинства и ограниченности. Учитывая это, совершенно не удивительно, что теория систем ныне включает в себя целый ряд подходов, различающихся по своему стилю и задачам.

Системная проблематика по существу сводится к ограничению применения традиционных аналитических процедур в науке. Обычно системные проблемы выражаются в полуметафизических понятиях и высказываниях, подобных, например, понятию «эмерджентная эволюция» или утверждению «целое больше суммы его частей», однако они имеют вполне определенное операциональное значение.  При применении «аналитической процедуры» некоторая исследуемая сущность разлагается на части, и, следовательно, впоследствии она может быть составлена или воссоздана из собранных вместе частей, причем эти процессы возможны как концептуально, так и материально. Это – основной принцип «классической» науки, который может осуществляться различными путями: разложением исследуемого явления на отдельные причинные цепи, поисками «атомарных» единиц в различных областях науки и т. д. Научный прогресс показывает, что эти принципы классической науки, впервые сформулированные Галилеем и Декартом, приводят к большим успехам при изучении широкой сферы явлений.

Применение аналитических процедур требует выполнения двух условий. Во-первых, необходимо, чтобы взаимодействие между частями данного явления отсутствовало или было бы пренебрежимо мало для некоторой исследовательской цели. Только при этом условии части можно реально, логически или математически «извлекать» из целого, а затем «собирать». Второе условие: отношения, описывающие поведение частей, должны быть линейными. Только в этом случае имеет место отношение суммативности, т. е. форма уравнения, описывающего поведение целого, такова же, как и форма уравнений, описывающих поведение частей; наложение друг на друга частных процессов позволяет получить процесс в целом и т. д.

Для образований, называемых системами, т. е. состоящих из взаимодействующих частей, эти условия не выполняются. Прототипом описания систем являются системы дифференциальных уравнений, в общем случае нелинейных. Систему, или «организованную сложность», можно описать через существование «сильных взаимодействий» (Rapoport [69]) или взаимодействий, которые «нетривиальны» (Simon [80]), т. е. нелинейны. Методологическая задача теории систем, таким образом, состоит в решении проблем, которые носят более общий характер, чем аналитически-суммативные проблемы классической науки.

Как уже отмечалось, существуют различные подходы к таким проблемам. Мы намеренно используем довольно расплывчатое выражение – «подходы», поскольку они логически неоднородны, характеризуются различными концептуальными моделями, математическими средствами, исходными позициями и т. д. Они, однако, согласуются в том, что все они являются теориями систем. Если оставить в стороне подходы в прикладных системных исследованиях, таких, как системотехника, исследование операций, линейное и нелинейное программирование и т. д., то наиболее важными являются следующие подходы.

«Классическая» теория систем применяет классическую математику. Ее цель – установить принципы, применимые к системам вообще или к их определенным подклассам (например, к закрытым и открытым системам); разработать средства для их исследования  и описания и применить эти средства к конкретным случаям. Учитывая достаточную общность получаемых результатов, можно утверждать, что некоторые формальные системные свойства относятся к любой сущности, которая является системой (к открытым системам, к иерархическим системам и т. д.), даже если ее особая природа, части, отношения и т. д. не известны или не исследованы. Примером могут служить обобщенные принципы кинетики, применимые, в частности, к популяциям молекул или биологических существ, т. е. к химическим и экологическим системам; уравнения диффузии, используемые в физической химии и для анализа процесса распространения слухов; применение понятия устойчивого равновесия и моделей статистической механики к транспортным потокам; аллометрический анализ биологических и социальных систем и т. д.

Использование вычислительных машин и моделирование. Системы дифференциальных уравнений, применяемые для «моделирования» или спецификации систем, обычно требуют много времени для своего решения, даже если они линейны и содержат немного переменных; нелинейные системы уравнений разрешимы только в некоторых частных случаях. По этой причине с использованием вычислительных машин открылся новый подход к системным исследованиям. Дело заключается не только в значительном облегчении необходимых вычислений, которые иначе потребовали бы недопустимых затрат времени и энергии, и замене математической изобретательности заранее установленными последовательностями операций. Важно еще и то, что при этом открывается доступ в такие области, где в настоящее время отсутствует соответствующая математическая теория и нет удовлетворительных способов решения. Так, с помощью вычислительных машин могут анализироваться системы, по свой сложности далеко превосходящие возможности традиционной математики; с другой стороны, вместо лабораторного эксперимента можно воспользоваться моделированием на вычислительной машине и построенная таким образом модель затем может быть проверена в реальном эксперименте. Таким способом Б. Гесс (Hess, 1968), например, рассчитал 14-звенную цепь реакций гликолиза в клетке на модели, содержащей более 100 нелинейных дифференциальных уравнений. Подобный анализ стал обычным делом в экономических разработках, при исследовании рынка и т. д.

Теория ячеек (compartment theory). Одним из аспектов системных исследований, который следует выделить, поскольку эта область разработана чрезвычайно подробно, является теория ячеек (Rescigno and Segre [73]), изучающая системы, составленные из подъединиц с определенными граничными условиями, причем между этими подъединицами имеют место процессы переноса. Такие ячеечные системы могут иметь, например, «цепную» или «сосковую» структуру (цепь ячеек или центральную ячейку,  сообщающуюся с рядом периферийных ячеек). Вполне понятно, что при наличии в системе трех и более ячеек математические трудности становятся чрезвычайно большими. В этом случае анализ возможен лишь благодаря использованию преобразований Лапласа и аппарата теорий сетей и графов.

Теория множеств. Общие формальные свойства систем и формальные свойства закрытых и открытых систем и т. д. могут быть аксиоматизированы в языке теории множеств (Masaroviс [60]; Maccia [58]). По математическому изяществу этот подход выгодно отличается от более грубых и специализированных формулировок «классической» теории систем. Связи аксиоматизированной теории систем с реальной проблематикой системных исследований пока выявлены весьма слабо.

Теория графов. Многие системные проблемы относятся к структурным и топологическим свойствам систем, а не к их количественным отношениям. В этом случае используется несколько различных подходов. В теории графов, особенно в теории ориентированных графов (диграфов), изучаются реляционные структуры, представляемые в топологическом пространстве. Эта теория применяется для исследования реляционных аспектов биологии (Rashevsky [70; 71]; Rosen [74]). В математическом смысле она связана с матричной алгеброй, по своим моделям – с тем разделом теории ячеек, в котором рассматриваются системы, содержащие частично «проницаемые» подсистемы, а вследствие этого – с теорией открытых систем.

Теория сетей в свою очередь связана с теориями множеств, графов, ячеек и т. д. Она применяется к анализу таких систем, как нервные сети (например, Rapoport [66]).

Кибернетика является теорией систем управления, в основе которых лежит связь (передача информации) между системой и средой и внутри системы, а также управление (обратная связь) функциями системы относительно среды. Как уже говорилось, кибернетические модели допускают широкое применение, но их нельзя отождествлять с теорией систем вообще. В биологии и других фундаментальных науках кибернетические модели позволяют описывать формальную структуру механизмов регуляции, например, при помощи блок-схем и графов потоков. Использование кибернетических моделей позволяет установить структуру регуляции системы даже в том случае, когда реальные механизмы остаются неизвестными и система представляет собой «черный ящик», определяемый только его входом и выходом. Таким образом, одна и та же кибернетическая схема может применяться к гидравлическим, электрическим, физиологическим и т. д. системам. Тщательно разработанная техническая теория сервомеханизмов применяется к естественным системам в ограниченном объеме [4; 47; 61]. 

Теория информации в смысле К. Шеннона и У. Уивера [78] опирается на понятие информации, математическое выражение для которой изоморфно выражению для негэнтропии в термодинамике. Считается, что понятие информации можно использовать в качестве меры организации [65]. Хотя теория информации имеет большое значение для техники связи, ее применения в науке до сих пор весьма незначительны. Главной проблемой остается выяснение отношения между информацией и организацией, между теорией информации и термодинамикой.

Теория автоматов представляет собой теорию абстрактных автоматов, имеющих вход, выход, иногда способных действовать методом проб и ошибок и обучаться. Общей моделью теории автоматов является машина Тьюринга, которая представляет собой абстрактную машину, способную печатать (или стирать) на ленте конечной длины цифры 1 и 0. Можно показать, что любой сколь угодно сложный процесс может моделироваться машиной Тьюринга, если этот процесс можно выразить конечным числом операций. В свою очередь то, что возможно логически (т. е. в алгоритмическом символизме), может также быть сконструировано – в принципе, но не всегда практически – автоматом (т. е. алгоритмической машиной).

Теорию игр [63], хотя она и несколько отличается от других рассмотренных системных подходов, все же можно поставить в ряд наук о системах. В ней рассматривается поведение «рациональных» игроков, пытающихся достичь максимальных выигрышей и минимальных потерь за счет применения соответствующих стратегий в игре с соперником (или природой). Следовательно, теория игр по существу рассматривает «системы», включающие антагонистические «силы».

Теория решений является математической теорией, изучающей условия выбора между альтернативными возможностями.

Теория очередей рассматривает оптимизацию обслуживания при массовых запросах.

Несмотря на неоднородность и явную неполноту проведенного рассмотрения, отсутствие достаточной четкости в различении моделей (например, моделей открытой системы, цепи обратной связи и т. д.) и математических формализмов (например, формализмов теорий множеств, графов, игр), такое перечисление позволяет показать, что существует целый ряд подходов к исследованию систем, а некоторые из них обладают мощными математическими методами. Системные исследования означают прогресс в анализе проблем, которые ранее не изучались, считались выходящими за пределы науки или чисто философскими.

Хорошо известно, что проблема соответствия между моделью и реальностью чрезвычайно сложна. Нередко мы располагаем тщательно разработанными математическими моделями, но остается неясным, как можно применять их в конкретном случае. Для  многих фундаментальных проблем вообще отсутствуют подходящие математические средства. Чрезмерные ожидания привели в последнее время к разочарованию. Так, например, кибернетика продемонстрировала свое влияние не только в технике, но и в фундаментальных науках; построила модели ряда конкретных явлений, показала научную правомерность телеологического объяснения и т. д. Тем не менее кибернетика не создала нового широкого «мировоззрения», оставаясь скорее расширением, чем заменой механистической концепции (см. [25]). Теория информации, математические основы которой детально разработаны, не смогла построить интересных приложений в психологии и социологии. Большие надежды возлагались на применение теории игр к вопросам войны и политики, но едва ли можно считать, что она улучшила политические решения и положение дел в мире. Эту неудачу можно было ожидать, учитывая, как мало существующие державы походят на «рациональных» игроков теории игр. Понятия и модели равновесия, гомеостазиса, регулирования и т. д. приложимы для описания процессов функционирования систем, но они неадекватны для анализа явлений изменения, дифференциации, эволюции, уменьшения энтропии, творчества и т. д. Это осознавал Кэннон, когда он допускал кроме гомеостазиса еще и «гетеростазис», характеризующий такие явления. Теория открытых систем широко применяется для описания явлений биологии (и техники), но необходимо предостеречь против неосмотрительного распространения ее на те области, для которых она не предназначена. Вполне очевидно, что отмеченные ограниченности системных научных подходов, существующих едва ли больше двадцати-тридцати лет, совершенно естественны. В конечном счете разочарование, о котором мы только что говорили, объясняется применением моделей, полезных в определенных аспектах, к проблемам метафизического и философского порядка.

Несмотря на то, что математические модели обладают важными достоинствами – четкостью, возможностью строгой дедукции, проверяемостью и т. д., не следует отказываться от использования моделей, сформулированных в обычном языке.

Вербальная модель лучше, чем отсутствие модели вообще или использование математической модели, которая при насильственном насаждении фальсифицирует реальность. Многие теории, получившие огромное влияние в науке, являются нематематическими по своему характеру (например, психоаналитическая теория), а в других случаях лежащие в их основе математические конструкции осознаются позднее и охватывают лишь отдельные аспекты соответствующих эмпирических данных (как в теории отбора).

Математика, по сути дела, сводится к установлению алгоритмов, которые более точны, чем алгоритмы обычного языка. История науки свидетельствует о том, что описание проблем на обычном языке часто предшествует их математической формулировке, т. е.  отысканию алгоритма. Приведем несколько хорошо известных примеров: знаки, используемые для обозначения чисел и процесса счета, эволюционировали от слов естественного языка к римским цифрам (полувербальным, несовершенным, полуалгебраическим) и далее – к арабской численной символике, в которой важное значение имеет положение знака; уравнения первоначально формулировались в словесной форме, затем – с использованием примитивного символизма, который мастерски применяли Диофант и другие основатели алгебры, и, наконец, в современном символизме; для многих теорий, например для теории Дарвина, определение математических основ происходит значительно позднее их создания. Вероятно, лучше иметь сначала какую-то нематематическую модель со всеми ее недостатками, но охватывающую некоторый незамеченный ранее аспект исследуемой реальности и позволяющую надеяться на последующую разработку соответствующего алгоритма, чем начинать со скороспелых математических моделей.

Таким образом, модели, выраженные в обычном языке, оставляют себе место в теории систем. Идея системы сохраняет значение даже там, где ее нельзя сформулировать математически или где она остается скорее «направляющей идеей», чем математической конструкцией. Например, у нас может не быть удовлетворительных системных понятий для социологии; однако само понимание того, что социальные сущности являются системами, а не суммами социальных атомов, или того, что история имеет дело с системами (хотя бы и плохо определенными), называемыми цивилизациями, которые подчиняются общим для систем принципам, подразумевает важную переориентацию в рассматриваемых научных областях.

Как мы видели ранее, в рамках «системного подхода» существуют и механистические, и организмические тенденции и модели, пытающиеся познать системы либо с помощью таких понятий, как «анализ», «линейная (включая круговую) причинность», «автомат» и т. д., либо при помощи понятий «целостность», «взаимодействие», «динамика» и им подобных. Эти два типа моделей не исключают друг друга и даже могут использоваться для описания одних и тех же явлений (см. [56]). Вместе с тем возникает вопрос, какая же точка зрения является более общей и фундаментальной, что по сути дела сводится к решению вопроса о машине Тьюринга как об абстрактном автомате.

Одна из возникающих в этой связи проблем – это проблема «громадных» («астрономических») чисел. Фундаментальное положение теории автоматов заключается в том, что события, которые можно описать конечным числом «слов», могут быть реализованы автоматом [64]. Здесь существенное значение имеет термин «конечный». По определению, автомат может реализовать конечные серии событий (сколь угодно большие), но не бесконечные. Что  произойдет, однако, если требуемое число шагов «астрономически» велико, т. е. не бесконечно, но превосходит, например, число частиц во Вселенной (оцениваемое величиной порядка 1080) или число событий, возможных за время существования Вселенной или некоторых ее частей? Такие «астрономические» числа встречаются во многих системных проблемах, связанных, с экспоненциальными, факториальными и другими взрывоподобно возрастающими функциями. Они встречаются даже при изучении систем с умеренным числом компонентов, взаимодействием между которыми нельзя пренебречь (ср. [3]). Для того чтобы «отобразить» их в машине Тьюринга, потребовалась бы столь большая лента, которая превышает наши не только практические, но и физические возможности.

Рассмотрим, например, ориентированный граф, состоящий из N вершин (Rapoport [67]). Между каждой парой вершин может существовать или не существовать связь (две возможности). Следовательно, имеется 2N(N–1) различных способов связать N вершин. Если N равно только 5, то число способов связи вершин превосходит один миллион. При N = 20 число способов связи превышает предполагаемое число атомов во Вселенной. Подобные же проблемы возникают, например, относительно возможного числа связей между нейронами (число нейронов в мозге человека оценивается величиной порядка 10 биллионов) и при анализе генетического кода (Repge [72]). В этом коде существует минимум 20 «слов» (нуклеотидных триплетов), образованных различными аминокислотами; код может содержать около миллиона единиц. Это дает 201 000 000 возможностей. Предположим, что лапласовскпй демон должен найти функциональное значение каждой комбинации, для чего ему пришлось бы провести именно такое число исследований. Однако во Вселенной существует только 1080 атомов и организмов. Предположим (Repge, 1962), что в некоторый момент на Земле имеется 1030 клеток. Если мы допустим далее, что каждую минуту возникает новое поколение клеток, то при возрасте Земли, равном 15 биллионам лет (1016 минут), полное число клеток равно 1046. Для того чтобы гарантировать получение максимального числа, допустим, что на 1020 планетах есть жизнь. Тогда с уверенностью можно считать, что во всей Вселенной было не более чем 1066 живых существ – очень большое число, но далеко не «астрономическое». Или другой пример [3]. Рассмотрим телевизионный экран (бесконечно упрощенный по сравнению с реальным) состоящий из 400 ламп, т. е. квадратную матрицу 20 x 20 лампочек. Число образов, которые могут появиться на таком экране, равно 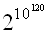, т. е. число порядка единицы с последующими 10120 нулями. Однако поскольку число атомов во Вселенной равно только 1080, то упомянутое число невозможно записать, даже если бы каждая цифра в нем выражалась одним атомом.

С другой стороны, согласно Харту (Hart [42]), человеческое творчество можно рассматривать как новую комбинацию из ранее  существовавших элементов. Если это так, то возможность новых изобретений возрастает, грубо говоря, как функция числа возможных размещений и сочетаний от числа имеющихся элементов, т. е. это возрастание является факториалом от числа элементов. В общем случае пределы автоматов становятся очевидными, если регуляция в системе направлена против «произвольного» числа нарушений, а не против одного нарушения или ограниченного их числа, т. е. против неопределенного числа ситуаций, которые невозможно «предвидеть». Этот случай широко представлен в эмбрионной (например, эксперименты Дриша) и нейронной (например, эксперименты Лешли) регуляциях. Регуляция здесь является результатом взаимодействия многих компонентов (см. [46]). Фон Нейман считает, что это, по-видимому, связано с тенденцией к «самовосстановлению» организмических систем в отличие от технических, или, выражаясь более современно, с тем, что они являются открытыми системами.

Совершенно очевидно из предшествующего рассмотрения, что именно эти свойства систем невыразимы в абстрактных моделях автомата, таких, как машина Тьюринга. Таким образом, механистическая концепция, на что давно указывали виталисты (например, Дриш), даже в ее современной и обобщенной форме (автомат Тьюринга) терпит крах при «столкновении» с регуляциями, направленными против «произвольных» нарушений, а также с событиями, в которых требуется «астрономическое» число шагов.

Проведенное рассуждение имеет определенное отношение к понятию, являющемуся, несомненно, фундаментальным для общей теории систем, а именно – к понятию иерархического порядка. Сейчас мы «видим» Вселенную как огромную иерархию, включающую элементарные частицы, атомные ядра, атомы, молекулы, высокомолекулярные соединения, изобилие структур между молекулами и клетками [90], клетки организма и надиндивидуальные организации. Такая иерархия проявляется как в «структурах», так и в «функциях». В конечном счете структура (т. е. порядок частей) и функция (т. е. порядок процессов) могут быть одним и тем же: в физическом мире вещество превращается в движение энергии, а в биологическом мире структуры являются выражением определенных процессов. В настоящее время система физических законов относится главным образом к области атомов и молекул (и их совокупностям в макрофизике). Очевидно, что эта область является лишь частью более широкого спектра. Законы организации и организующие силы в субатомной и супермолекулярной областях изучены недостаточно. Происходит вторжение как в субатомный мир (физика высоких энергий), так и в супермолекулярный (физика высокомолекулярных соединений), но этот процесс, по-видимому, находится в своей начальной стадии. Это проявляется, с одной стороны, в нынешней неразберихе с элементарными частицами и, с другой стороны – в отсутствии в настоящее время  физического понимания структур, видимых под электронным микроскопом, и в отсутствии «грамматики» генетического кода.

Общая теория иерархического порядка, очевидно, будет важнейшей составной частью общей теории систем. Принципы иерархического порядка могут быть сформулированы в вербальном языке [53]; уже существуют некоторые полуматематические идеи на этот счет, связанные с матричной теорией [80], и соответствующие формулировки в терминах математической логики [94]. Большое значение, видимо, будет иметь исчисление иерархии. Проблема иерархического порядка тесно связана с вопросами эволюции, араморфоза и меры организации; последнюю, видимо, невозможно адекватно выразить ни в энергетических терминах (энтропия), ни в терминах теории информации (биты). В конечном счете динамика и иерархический порядок могут представлять собой одно и то же.

Таким образом, существует целый ряд моделей систем, более или менее развитых и разработанных. Некоторые понятия, модели и принципы общей теории систем, такие, как иерархический порядок, прогрессирующая дифференциация, обратная связь, системные характеристики, определяемые теориями множеств и графов, и т. д., широко применимы к материальным, психологическим и социокультурным системам; другие, как, например, понятие открытой системы, определяемой обменом веществ, ограничены определенными подклассами систем. Как показывает практика прикладного анализа систем, применение различных моделей систем зависит от специфики рассматриваемых в том или ином случае проблем и соответствующих операциональных критериев.

Литература

1. Асkоff R.L. Games, decision, and organizations // General Systems. Vol. IV. 1959. P. 145–150.

2. Afanasjev W.G. Űber Bertalanffys «organismische Konzeption» // Deutsche Zeitschrift fűr Philosophie. Bd. 10. 1962. S. 1033–1040.

3. Ashby W.R. Constraint Analysis of Many-Dimensional Relation // University of Illinois. Electrical Engineering Research Laboratory. Technical Report. № 2. May 1964. Urbana.

4. Вауliss L.E. Living Control Systems. San Francisco: Freeman, 1966.

5. Beckner M. The Biological Way of Thought. New York: Columbia University Press, 1959.

6. Вendmann A. Die «organismische Auffassung» Bertalanffys. // Deutsche Zeitschrift fűr Philosophie. Bd. 11. 1963. S. 210–222.

7. Вendmann A. L. von Bertalanffys organismische Auffassung des Lebens in ihren philosophischen Konsequenzen. Jena: Gustav Fischer Verlag, 1967.

8. Bernal J.D. Science in History. 2rd ed. London: Watts, 1957.

9. Bertalanffy L. von. Nikolaus von Kues. Műnchen: G. Műller, 1928. 

10. Bertalanffy L. von. Modern Theories of Development. 1st ed. – 1928. Transl. by J. H. Woodger. New York: Harper Torchbooks, 1962.

11. Bertalanffy L. von. Theoretische Biologie. Bd. I–II. Berlin: Borntraeger, 1932, 1942; 2nd ed. Bern: Francke, 1951.

12. Bertalanffy L. von. Das Weltbild der Biologie. – Arbeitskreis Biologie. // Weltbild und Menschenbild / S. Moser (Ed.). Salzburg: Tyrolia Verlag, 1948.

13. Bertalanffy L. von. Zu einer allgemeinen Systemlehre // Blatter fűr deutsthe Philosophie. Bd. 18. ą 3/4, 1945. Extract in: Biologia Generalis. Vol. 19. 1949. P. 114–129.

14. Bertalanffy L. von. Das biologische Weltbild. Bern: Francke, 1949. English: Problems of Life. New York: Harper Torchbooks, 1960.

15. Bertalanffy L. von. An Outline of General System Theory // British Journal for Philosophy of Science. Vol. I. № 2. 1950. P. 139–164.

16. Bertalanffy L. von. General System Theory. // General Systems. 1956. Vol. I.

17. Bertalanffy L. von. General System Theory – A Critical Review // General Systems. Vol. VII. 1962. P. 1–20.

18. Bertalanffy L. von. General System Theory and Psychiatry // American Handbook of Psychiatry. Vol. 3 / S. Arieti (Ed.). New York: Basic Books, 1966. P. 705–721.

19. Bertalanffy L. von. Robots, Men and Minds. New York: Braziller, 1967.

20. Bertalanffy L. von, Hempel C.G., Jоnas R.E.H. General System Theory: A New Approach to Unity of Science. // Human Biology. Vol. 23. 1951. P. 302–361.

21. Вlandinо G.S.J. Problemi e dottrine di biologia theorica. Bologna: Minerva Medica, 1960.

22. Воffeу Р.М. Systems Analysis: No Panaces for Nation's Domestic Problems // Science. Vol. 158. 1967. P. 1028–1030.

23. Воguslaw W. The New Utopians. New York: Prentice-Hall, Englewood Cliffs, 1965.

24. Воulding K.D. The Organizational Revolution. New York: Harper, 1953.

25. Bronowski J. Review of «Brains, Machines and Mathematics» by M. A. Arbib // Scientific American.. V. 130–134. 1964.

26. Buckley W. (Ed.). Modern Systems Research for the Behavioural Scientist. Chicago: Aldine Publ. Co., 1967.

27. Сannоn W.B. Organization for Physiological Homeostasis // Physiological Review. 1929. Vol. 9. P. 397.

28. Сannon W.B. The Wisdom of the Body. New York: Norton, 1932.

29. Carter L.J. Systems Approach: Political Interest Rises // Science. Vol. 153. 1966. P. 1222–1224.

30. Commoner R. In Defense of Biology // Science. Vol. 133. 1961. P. 1745–1748.

31. De-Shalit A. Remarks on Nuclear Structure. // Science. Vol. 153. 1966. P. 1063–1067.

32. Dоbzhanskу Т. Are Naturalists Old-Fashioned? // American Naturalist. Vol. 100. 1966. P. 541–550.

33. Dubоs R. Environmental Biology. // Bioscience. Vol. 14. 1964. P. 11–14.

34. Dubоs R. We are Slaves to Fashion in Research // Scientific Research. 36–37. January, 1967. P. 54. [c. 51]

35. Elsasser W. Atom and Organism. Princeton: Princeton University Press, 1966.

36. Flannerу К.V. Culture History v. Cultural Process: A debate in American archaeology. // Scientific American. Vol. 217. 1907. P. 119–122.

37. Frank L.K., Hutсhinsоn G.E., Livingstоne W.K., Mс Сullосh W.S., Wiener N. Teleological mechanisms. // Transations. New York: Academy of Sciences. V. 50. 1948.

38. Gilbert E.N. Information Theory after 18 years // Science. Vol. 152. 1966. P. 320–326.

39. Grау W., Rizzо N.D., Duhl F.D. (Eds). General Systems Theory and Psychiatry. New York: Little Brown. In press.

40. Grinker R.R. (Ed.). Toward a Unified Theory of Human Behaviour. 2nd ed. New York: Basic Books, 1967.

41. Hahn E. Aktuelle Entwicklungstendenzen der soziologischen Theorie // Deutsche Zeitschrift fűr Philosophie. Bd. 15. ą 2. 1967. S. 178–191.

42. Hart H. Social Theory and Social Change. // Symposium on Sociological Theory / L. Gross (Ed.). Evanston: Row, Peterson, 1959. P. 196–238.

43. Hempel C.G. Aspects of Scientific Explanation and other Essays in the Philosophy of Science. New York: Free Press, 1965.

44. Hess W.R. Die Motorik als Organisationsproblem. // Biologisches Zentralblatt. Bd. 61. 1941.

45. Hess W.R. Biomotorik als Organisationsproblem. I–II. // Naturwissenschaften. Bd. 30. 1942. S. 441–448, 537–541.

46. Jeffries L.A. Cerebral Mechanisms in Behaviour. The Hixon Symposium. New York: Wiley, 1951.

47. Кalmus H. (Ed.). Regulation and Control in Living Systems. Now York: Wiley, 1966.

48. Кamarуt J. Die Bedeutung der Theorie des offenen Systems in der gegenwartigen Biologie. // Deutsche Zeitschrift fűr Philosophies. Bd. 9. 1961. S. 2040–2059.

49. Кamarуt J. Ludwig von Bertalanffy a synteticke smery v zapadni biologii. // Filosoficke problemy moderni biologie / J. Kamaryt (Ed.). Prag: Ceskoslovenska Akademie Ved, 1963. Str. 60 – 105.

50. Канаев П.П. Очерки из истории проблемы морфологического типа от Дарвина до наших дней. М.– Л., 1966.

51. Кőhler W. Die physischen Gestalten in Ruhe und im stationaren Zustand. Erlangen, 1924.

52. Кőhler W. Zum Problem der Regulation. // Roux Archiv. Bd. 112. 1927.

53. Коestler A. The Ghost in the Machine. London: Hutchinson, 1967.

54. Кuhn T.S. The Structure of Scientific Revolutions. Chicago, University of Chicago Press, 1962.

55. Левада Ю.А. Кибернетические методы в социологии // Коммунист. 1965. № 14.

56. Locker A. Reaktionen metabolisierender Sysleme auf expcrimentelle Beeinflussung. Reiz und Schadigung. // Helgolander wissenschaftliche Meeresuntersuchungen. Bd. 9. 1964. S. 38–107.

57. Lоtka A.J. Elements of Physical Biology. 1st ed. 1925; 2nd ed. – New York: Dover, 1956.

58. Mассia E.S., Mассia G.S. Development of Educational Theory Derived from Three Educational Theory Models. Project 5-0638. Columbus, Ohio: Ohio State Research Foundation, 1966. 

59. Menninger К., Maуman M., Pruуser Р. The Vital Balance. New York: Viking Press, 1963.

60. Mesarоviс M.D. Foundations for General Systems Theory. // Views on General Systems Theory / M. D. Mesarovic (Ed.). New York: Wiley, 1964. P. 1–24 (русский перевод: Общая теория систем. М.: Мир, 1966).

61. Milsum J.H. Biological Control Systems Analysis. New York: McGraw Hill, 1966.

62. Nagel E. The Structure of Science. London: Routledge and Kegan Paul, 1961.

63. Neumann J. von, Mоrgenstern O. Theory of Games and Economic Behaviour. Princeton; New York: Princeton University Press, 1947.

64. Neumann J. von. The general and logical theory of automata // Celebral Mechanisms in Behaviour.The Hixon Symposium / A. Jeffried (Ed.). New York: Wiley, 1951.

65. Quastler H. (Ed.). Information Theory in Biology. Urbana: University of Illinois Press, 1955.

66. Rapоpоrt A. Outline of a probabilistic approach to animal sociology. I–III. // Bulletin of Mathematical Biophysics. Vol. 11. P. 183–196, 273–281; Vol. 12. P. 7–17; 1949–1950.

67. Rapоpоrt A. Uses and Limitations of Mathematical Models in Social Sciences // Symposium on Sociological Theory / L. Gross (Ed.). Evanston: Row, Paterson, 1959. P. 348–372.

68. Rapоpоrt A. Critiques of Game Theory // Behavioral Science. Vol. 4. 1959. P. 49–66.

69. Rapoport A. Mathematical Aspects of General Systems Theory // General Systems. Vol. XI. 1960. P. 3–11.

70. Rashevskу N. Mathematical Biophysics. 2nd ed. Chicago: University of Chicago Press, 1948.

71. Rashevsky N. Topology and life. In search of general mathematical principles in biology and sociology. // General Systems. Vol. I. 1956. P. 123–138.

72. Repge R. Grenzen einer informationstheoretischen Interpretation des Organismus. // Giessener Hochschulblalter. Bd. 6. № 3/4. 1962.

73. Resсignо A., Segre G. Drug and Tracer Kinetics. Waltham; Blaisdell, 1966.

74. Rosen R. A Relational Theory of biological systems. I–II. // General Systems. Vol. V. 1960. P. 29–35, 35–43.

75. Ruesсh J. Epilogue // Toward A Unified Theory of Human Behaviour / R. R. Grinker (Ed.). 2nd ed. New York: Basic Books, 1967. P. 376–390.

76. Sсhaffner K.F. Antireductionism and Molecular Biology // Science. Vol. 157. 1967. P. 644 – 647.

77. Scott W.G. Organization Theory: An overview and an appraisal // Organizations: Structure and Behaviour  / J. A. Litterer (Ed ). New York: Wiley, 1963. P. 13–26.

78. Shannоn C., Weaver W. The Mathematical Theory of Communication. Urbana: University of Illinois Press, 1949 (русский перевод: Шеннон К.Э. Работы по теории информации и кибернетике. М., 1963).

79. Shaw L. System Theory. // Science. Vol. 149. 1965. P. 1005.

80. Simоn H.A. The architecture of complexity // General Systems. Vol. X. 1965. P. 63–76. 

81. Swith V.E. (Ed.). Philosophical Problems in Biology. New York: St. John's University Press, 1966.

82. Sоrоkin P.А. Contemporary Sociological Theories. 1st ed. – 1928; 2nd ed. – New York: Harper Torchbooks, 1964.

83. Sоrоkin P.А. Sociological Theories of Today. New York; London: Harper and How. 1966.

84. Spengler O. Der Untergang des Adendlandes. Műnchen: Beck, 1919, 1921 (русский перевод: Шпенглер О. Закат Европы. М., 1926).

85. Szent-Győrgyi A. Teaching and Expanding Knowledge // Science. Vol. 146. 1964. P. 1278–1279.

86. Toynbee A.A. Study of History. Vol. XII. Reconsiderations (1961). New York: Galaxy, 1964.

87. Тribinо S.E.M.G. de. Una Nueva Orientacion de la Filosoiia Biologica: El Organicismo de Luis Bertalanffy. Primer premio «Miguel Cane». Buenos Aires: Cursos у Conferencias, 1946.

88. Ungerer E. Die Wissenschaft vom Lehen. Eine Geschichte der Biologie. Bd. III. Freiburg: Műnchen: Alber, 1966.

89. Wagner R. Das Regelproblem in der Biologie. Stuttgart: Thieme, 1954.

90. Wiess P. From Cell to Molecule. // The molecular Control of Cellular Activity / J. M. Allen (Ed.). New York; Toronto; London, 1962.

91. Whitehead A. Science and Modern World. 1st ed. – 1925; 2nd ed. – New York: Macmillan, 1953.

92. Wiener N. Cybernetics. New York: Wiley, 1948 (русское издание: Винер Н. Кибернетика. М., 1958).

93. Wolfe H.B. Systems Analysis and Urban Planning – the San Francisco Housing Simulation Model // Transactions of the New York Academy of Sciences. Ser. II. Vol. 29. № 8. 1967. P. 1043–1049.

94. Wооdger J.H. The «Concept of Organism» and the Relation between Embryology and Genetics. I–III. // Quarterly Review of Biology. Vol. 5/6. 1930/1931.