Арифметико-логическое устройство (АЛУ) является одним из основных узлов вычислительной системы (в том числе микропроцессорной). Назначением этого устройства является формирование результата арифметических и логических операций над операндами, подающимися на его вход. В микропроцессорах АЛУ используется для вычисления результата выполнения арифметической или логической команды. При этом операндами могут являться как значения регистров процессора, так и содержимое внешней памяти, внешнего устройства, или даже непосредственное значение. Поскольку  АЛУ, как правило, способно выполнять несколько операций, выбор между ними выполняется на основе анализа кода выполняемой команды.

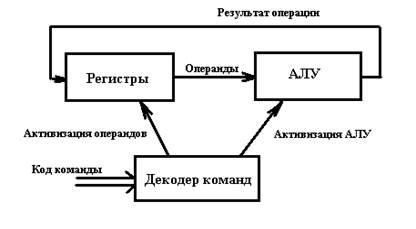
Схема взаимодействия АЛУ с другими узлами микропроцессора показана на рис. 5.12.

Рис. 5.12 Схема взаимодействия АЛУ с другими узлами микропроцессора

Поскольку большинство арифметических и логических операций требуют двух операндов, целесообразно разделить непосредственно АЛУ и устройство выбора операндов среди всех значений, доступных внутри процессора на момент исполнения команды. Такое устройство выбора существенно зависит от количества регистров процессора, наличия дополнительных устройств и системы команд процессора. Поэтому целесообразно выполнить разработку АЛУ таким образом, чтобы оно использовало только два операнда, а выбор нужных операндов выполнять с помощью другого модуля. Основными командами с двумя операндами, реализуемыми с помощью АЛУ, являются:

Далее перечислены команды, выполняемые над одним аргументом. Они вводятся в систему команд для повышения производительности процессора при исполнении типовых вычислительных алгоритмов.

Различие между арифметическим и логическим сдвигом связано с одним из вариантов представления чисел – так называемым дополнительным двоичным кодом. Это представление позволяет представлять числа со знаком в регистрах процессора и выполнять операции с ними единообразно, не рассматривая отдельно положительные и отрицательные значения.

В качестве примера рассмотрим вычисление выражения 0 – 1, где числа представлены в 8-разрядном двоичном виде.

_00000000

 00000001

 ________

 11111111

При выполнении вычитания требуется произвести заем из старшего (девятого) разряда, который в уменьшаемом отсутствует. При этом получаемое число может рассматриваться и как 25510, и как –1 в дополнительном двоичном коде. В качестве проверки можно выполнить операцию 1 + (–1)

00000001

11111111

________

00000000

При этом сумма в действительности должна быть представлена как 25610=1000000002, однако старший разряд не может быть записан в 8-разрядный регистр. Это свойство дополнительного двоичного кода и дает возможность применять его для представления отрицательных чисел. Нетрудно понять, что граница между положительными и отрицательными числами может быть выбрана различным образом (например, 111111102 может рассматриваться и как 25410, и как –210). На практике обычно считается, что число с установленным старшим разрядом является отрицательным. Таким образом, 8-разрядный регистр может представлять числа в диапазоне –128..+12710.

Рассмотрев формат представления чисел в дополнительном двоичном коде, можно прокомментировать некоторые команды из табл.2. Например, смена знака, описанная в таблице как NEGATE, для подобных чисел выполняется следующим образом: все разряды двоичного числа инвертируются, затем к полученному результату прибавляется 1. Справедливость этого правила рекомендуется проверить на примерах чисел 1/–1, 2/-2 и т.д.

С использованием старшего разряда в качестве знака числа связаны различия между арифметическим и логическим сдвигом. Сдвиг двоичного представления числа обычно используется для быстрого умножения (сдвиг влево) или деления (сдвиг вправо) на целую степень двойки. В этом также легко убедиться, рассмотрев в качестве примера сдвиг числа 810 = 000010002 на два разряда вправо. Такой сдвиг соответствует делению на 4 (каждый из сдвигов означает деление на 2), и результатом сдвига будет 000000102=210, что соответствует ожидаемому результату.

Однако для числа 111111102=–210 простой сдвиг на один разряд вправо дает в результате 011111112=12710, что не соответствует ожидаемому результату в –1. Поэтому с целью сохранения знака числа при его сдвиге вправо самый старший разряд не изменяется (но копируется в следующий за ним). Такой вариант сдвига, называемый арифметическим, позволяет корректно делить на целые степени 2 как положительные, так и отрицательные числа.

При сдвиге влево (умножении на целые степени 2) подобные проблемы не возникают, поэтому арифметический и логический сдвиги влево не различаются по реализации (хотя и могут присутствовать в ассемблерных мнемониках процессоров в качестве формально различных команд).

Команды ротации (вращения) имеют схожее со сдвигом действие, за исключением того, что в освобождающийся разряд вдвигается не нулевой бит, а тот, который в процессе выполнения команды выходит за пределы разрядной сетки.

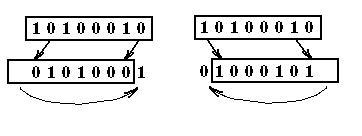
Рис. 5.13 Реализация команд вращения

Ряд арифметических команд требуют для реализации дополнительные аппаратные ресурсы или используются для поддержки операций с числами, имеющими бОльшую разрядность, чем у регистров процессора и АЛУ. Ряд этих команд представлен ниже.

Умножение и деление относятся к привычным действиям арифметики, однако их реализация требует существенно большего количества аппаратных ресурсов, чем для сложения и вычитания. Поэтому операции умножения и деления присутствуют не во всех типах микропроцессоров. Часто встречаются процессоры, в которых аппаратно реализовано только умножение, являющееся основой для программной реализации цифровых фильтров.

Сложение и вычитание с учетом переноса связано с механизмом обработки чисел, разрядность которых больше, чем допустимая разрядность операндов АЛУ.

  =  Перейти к содержанию  =