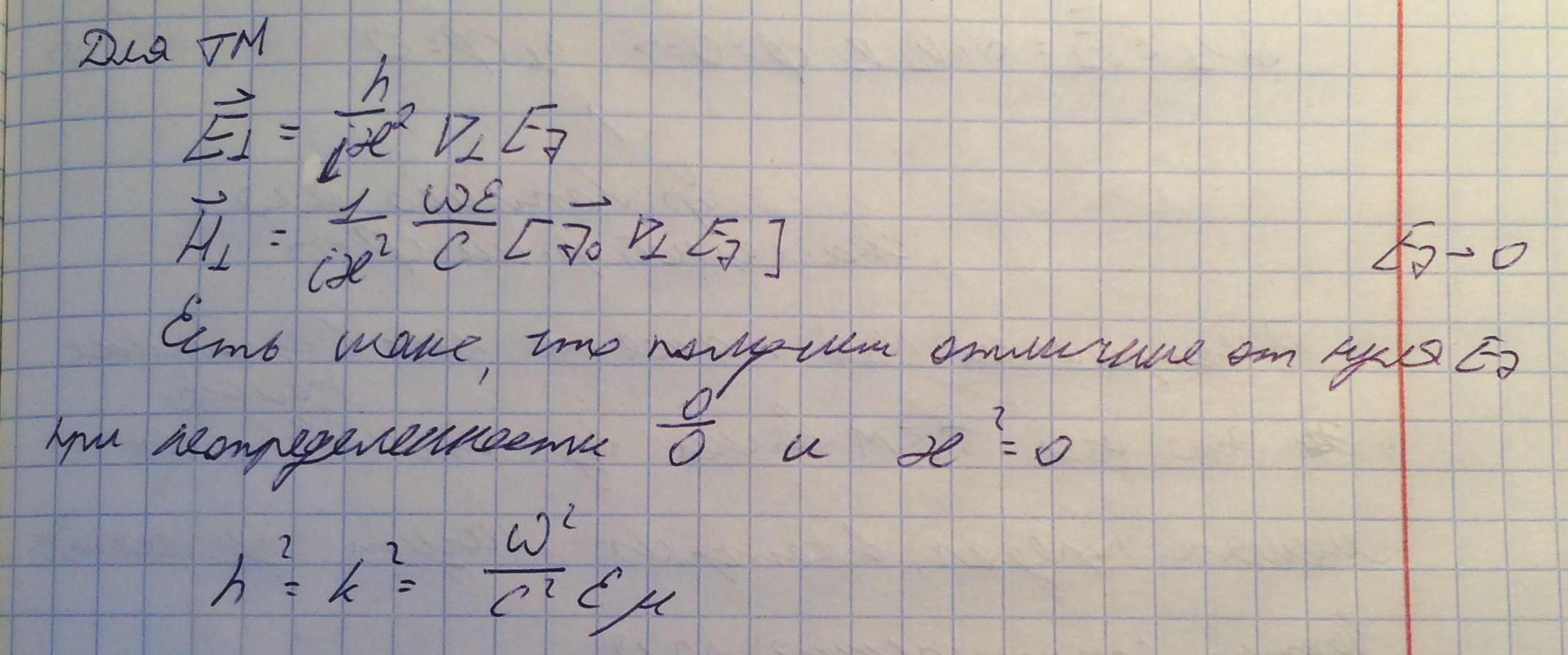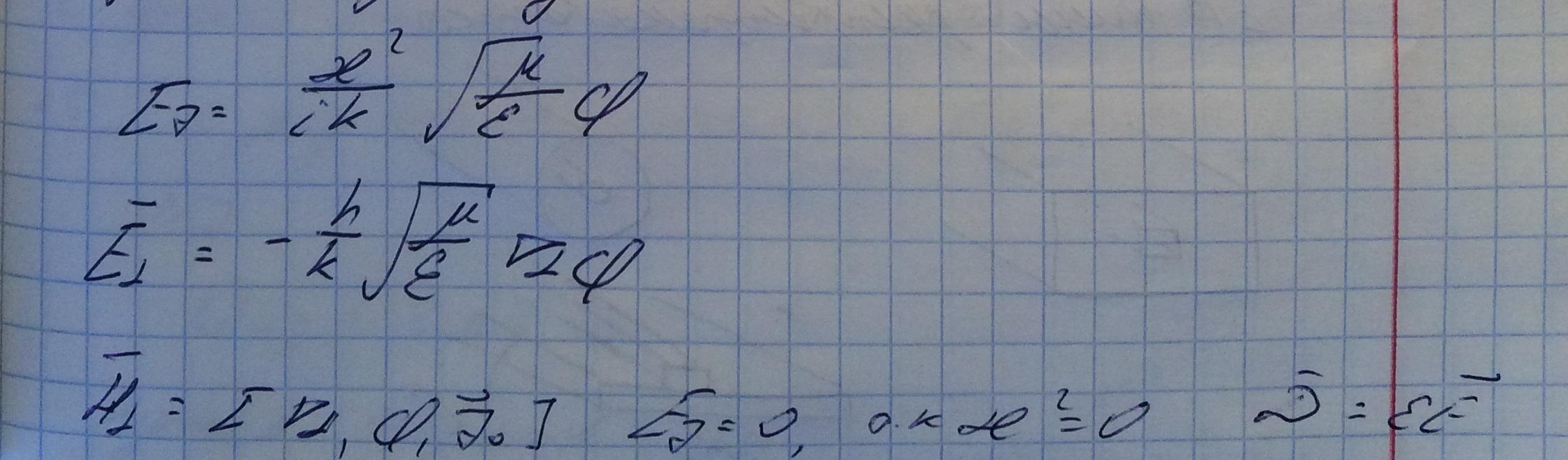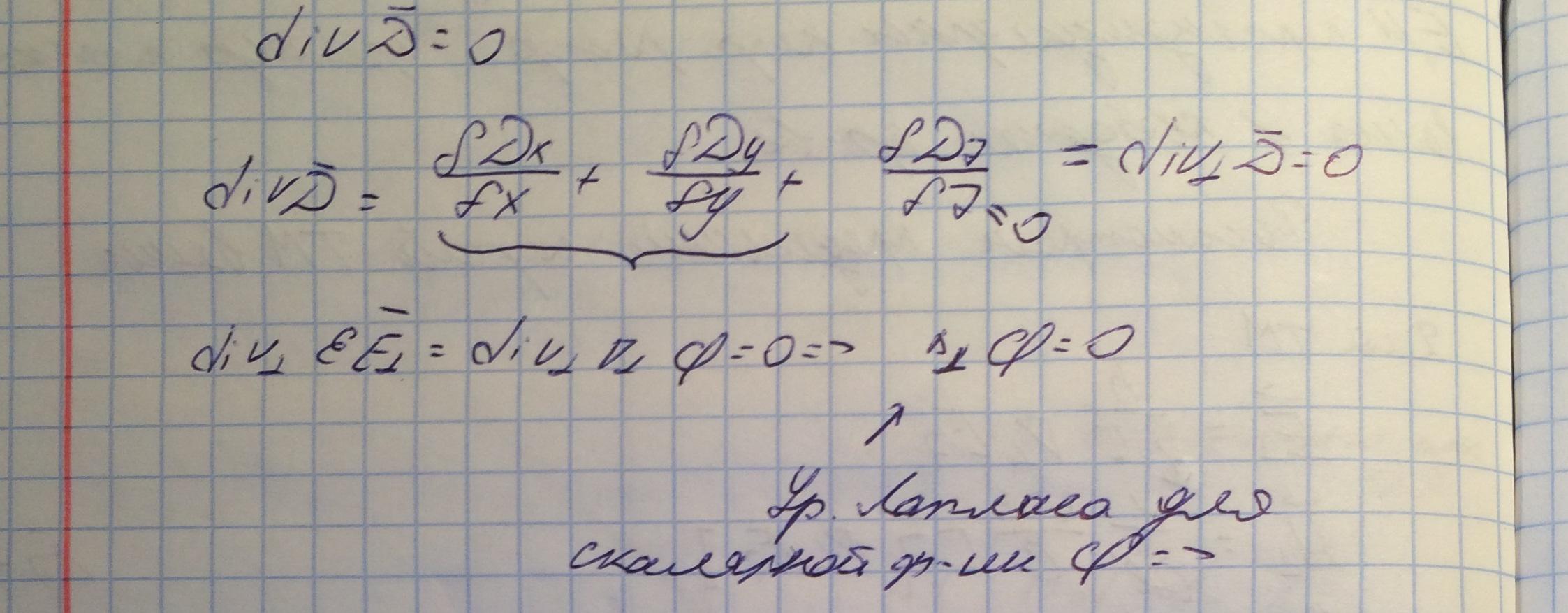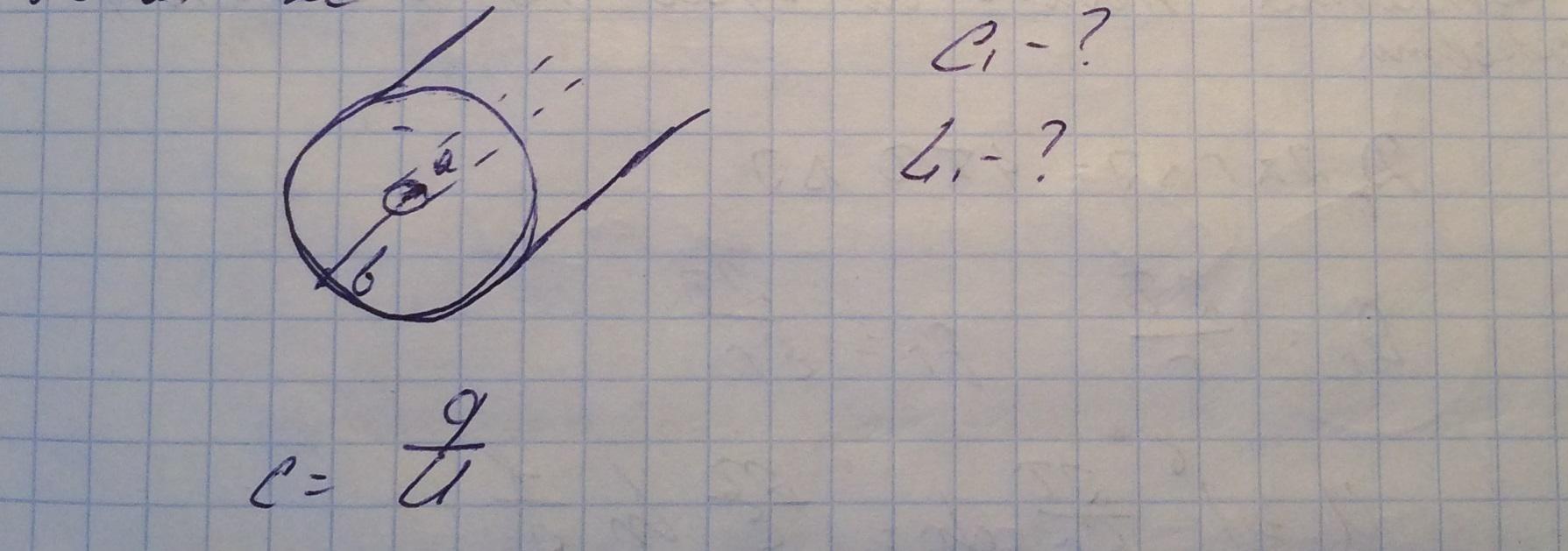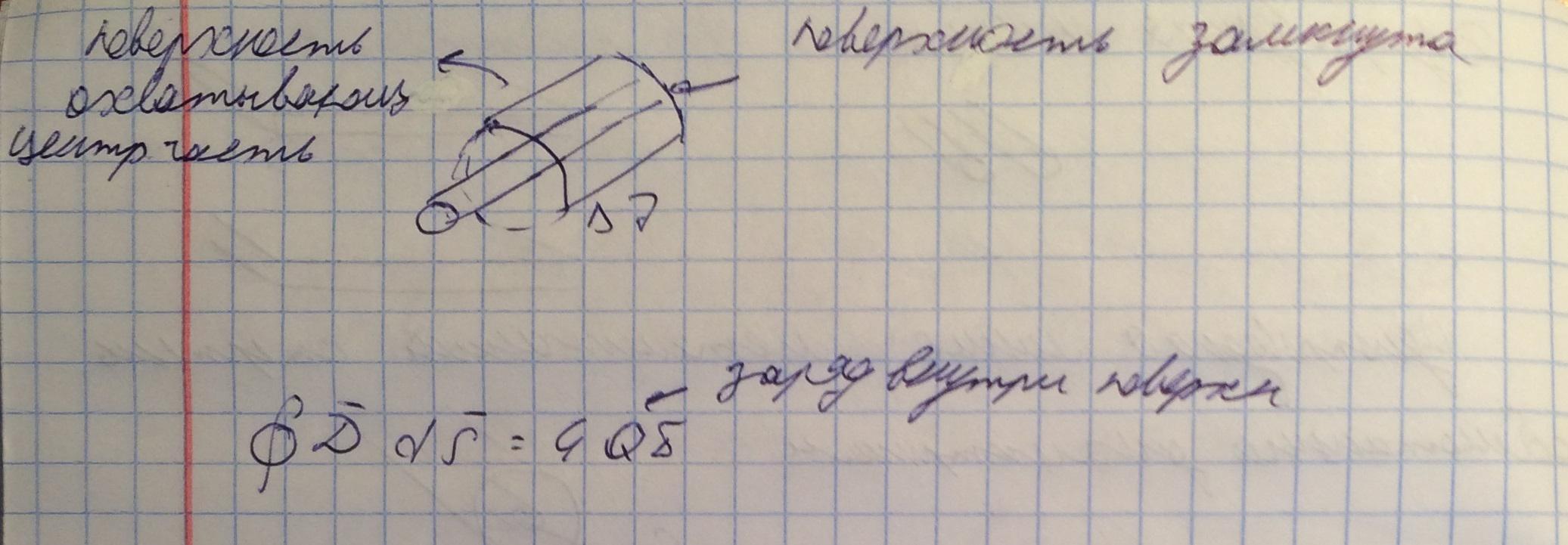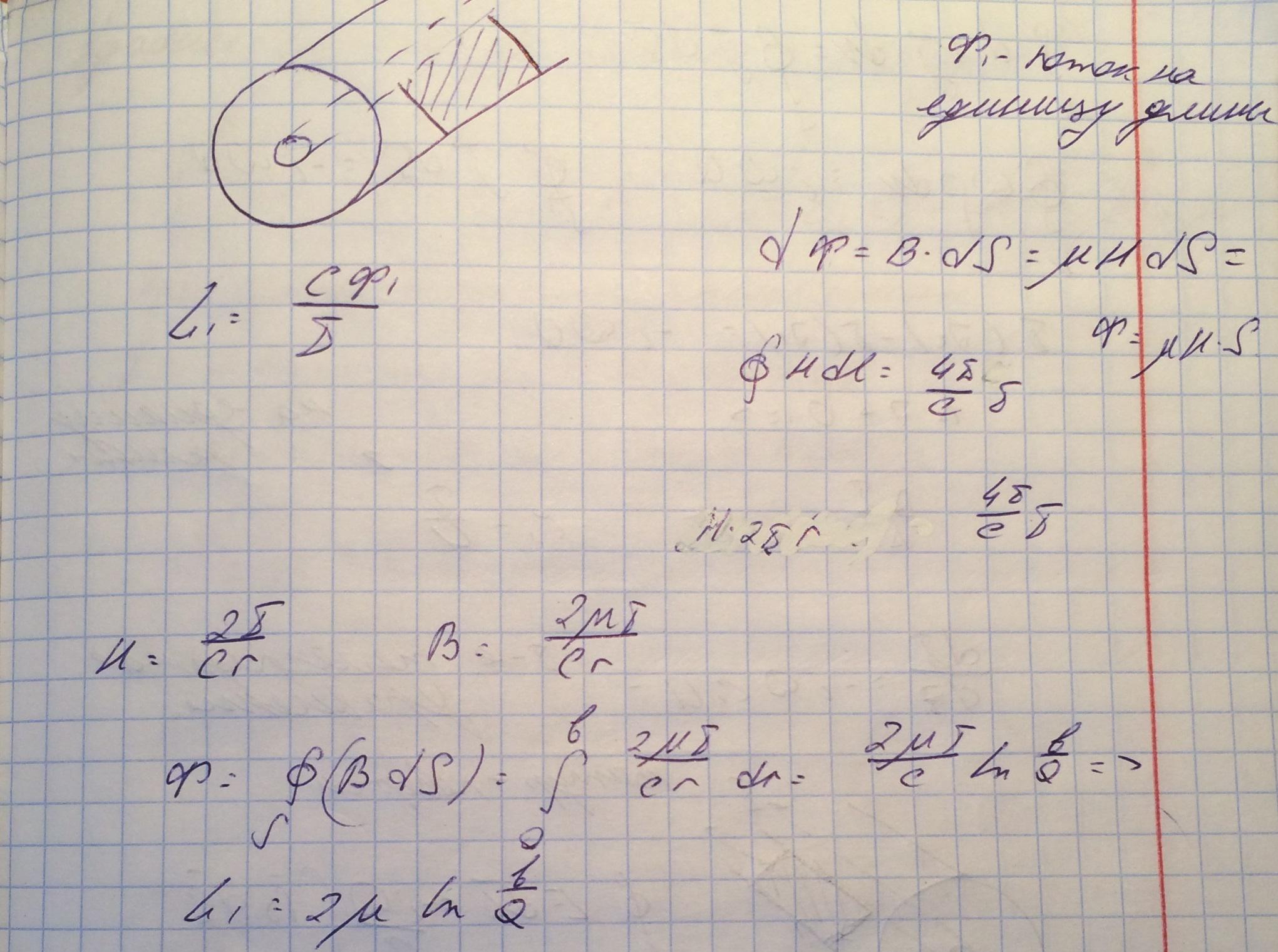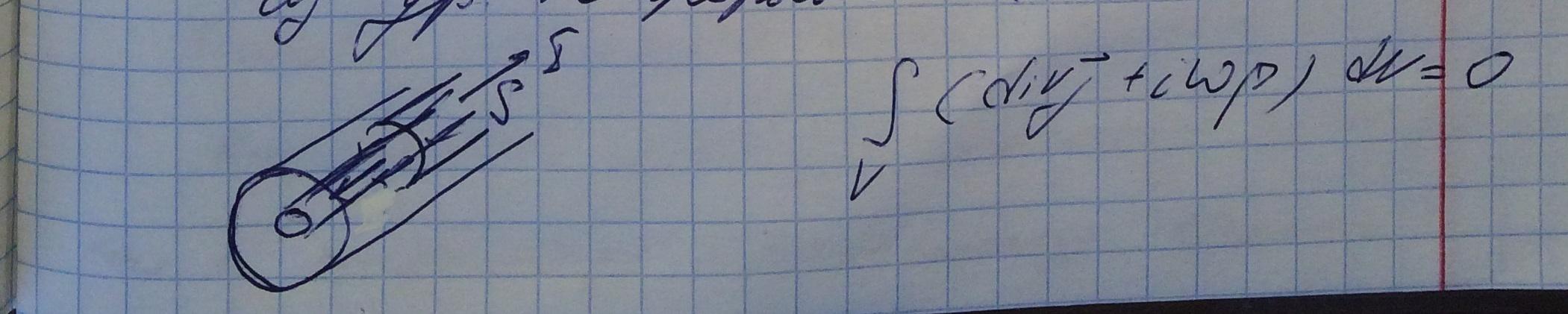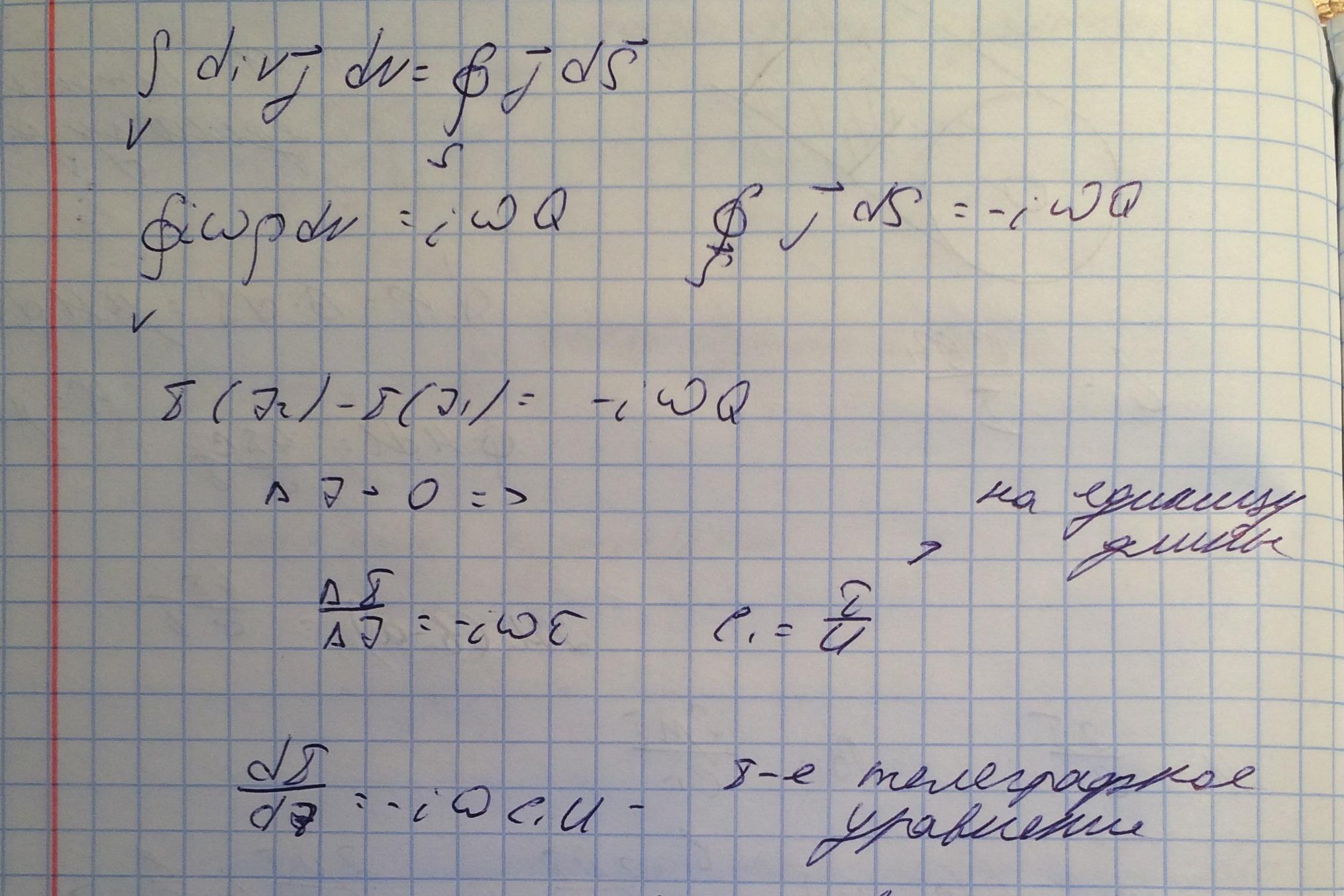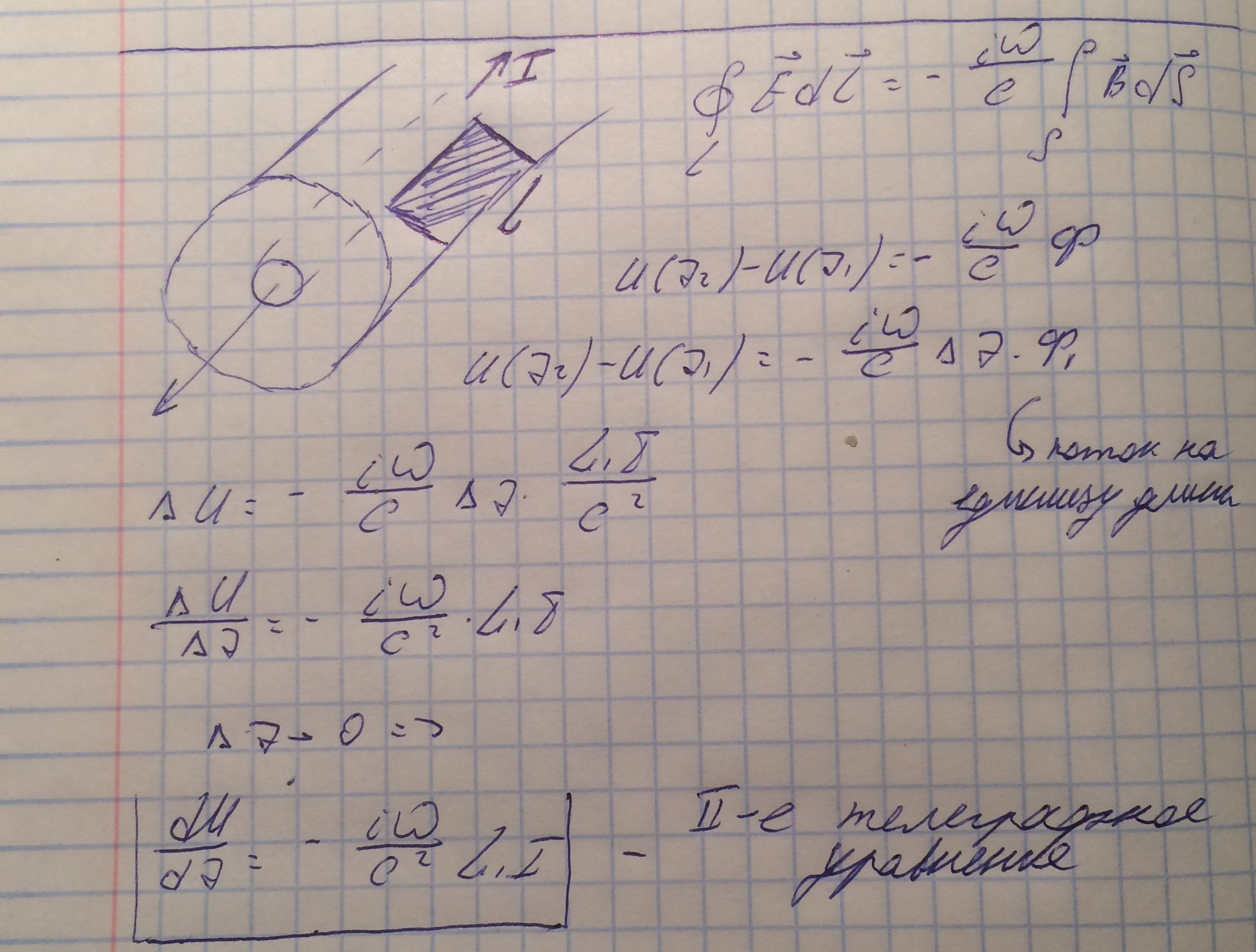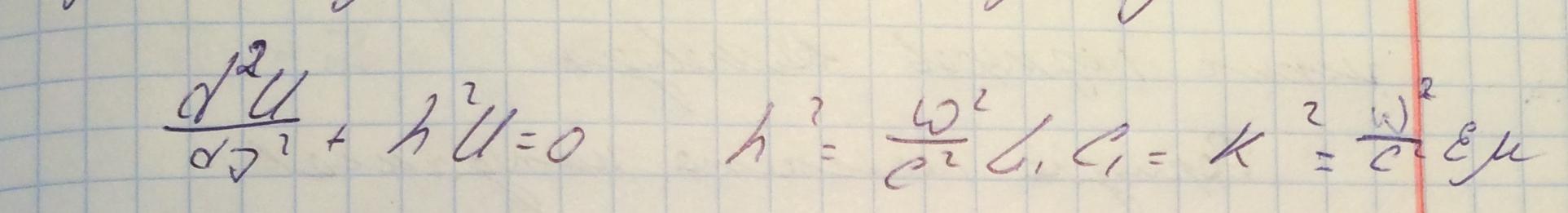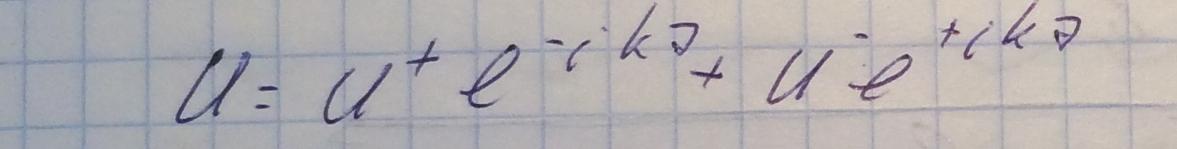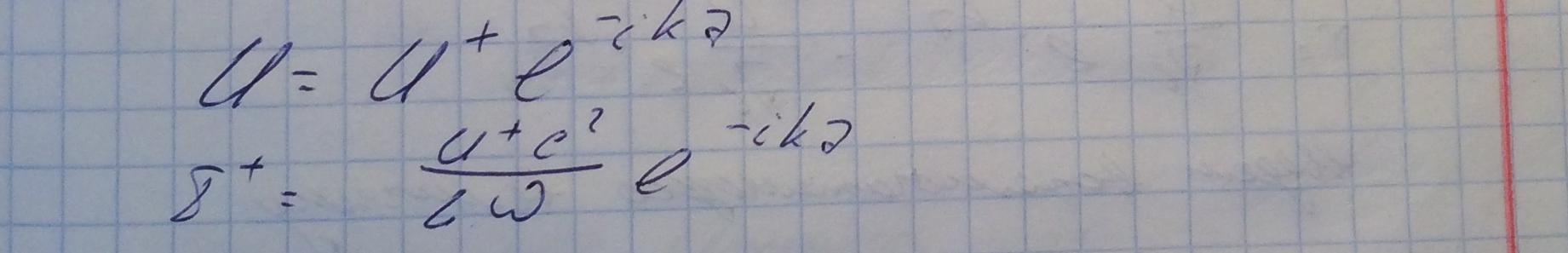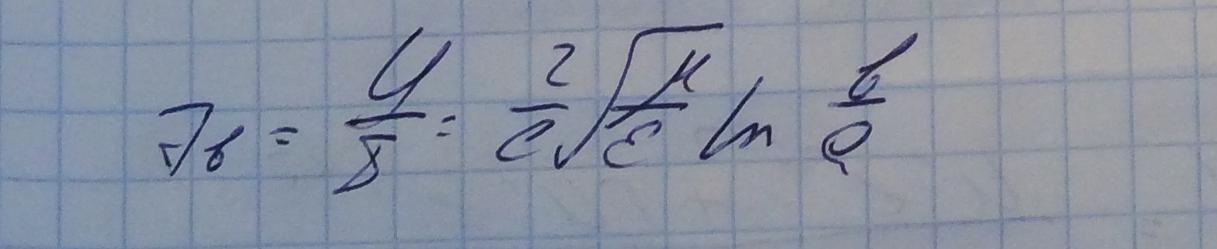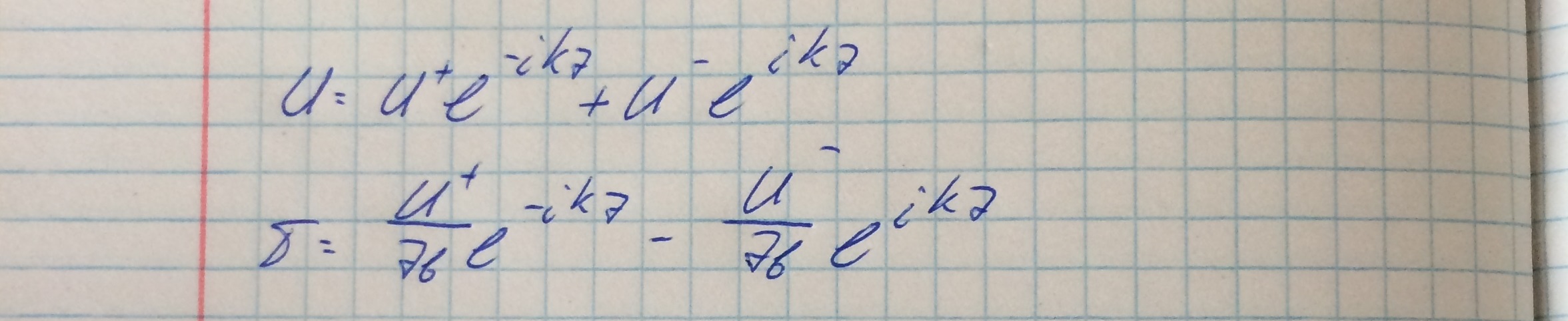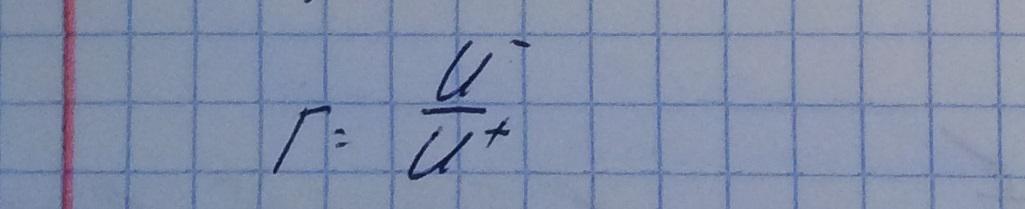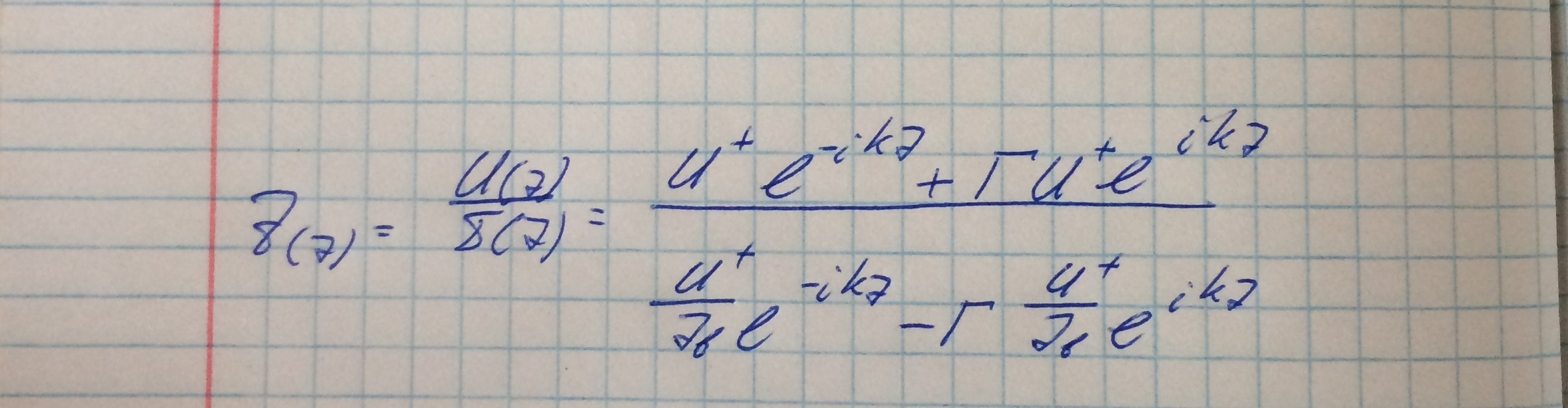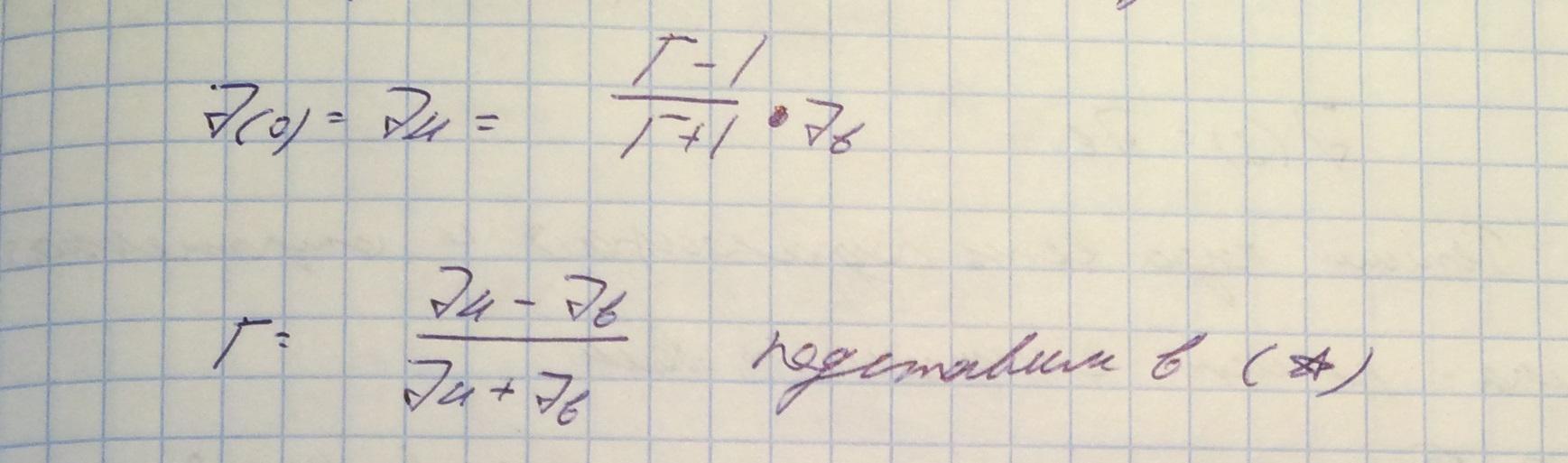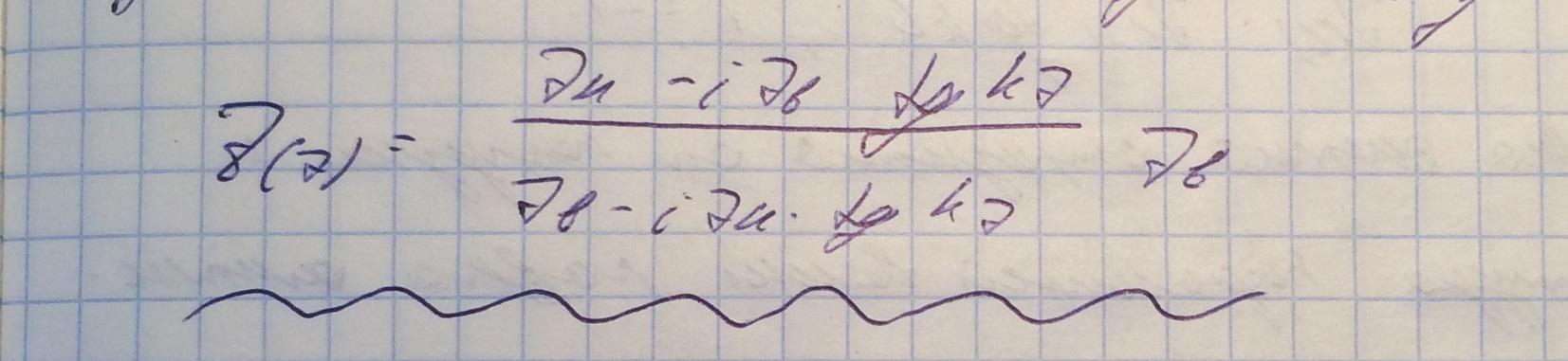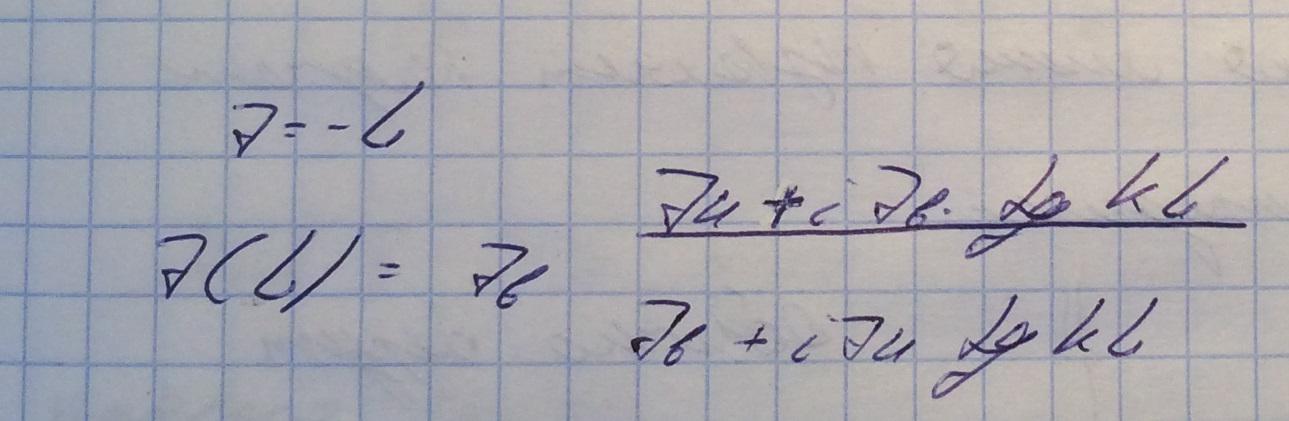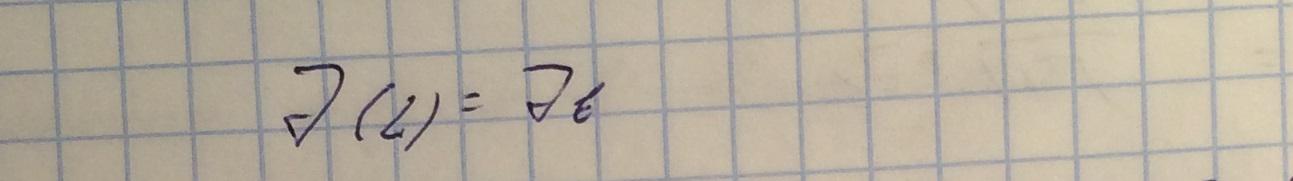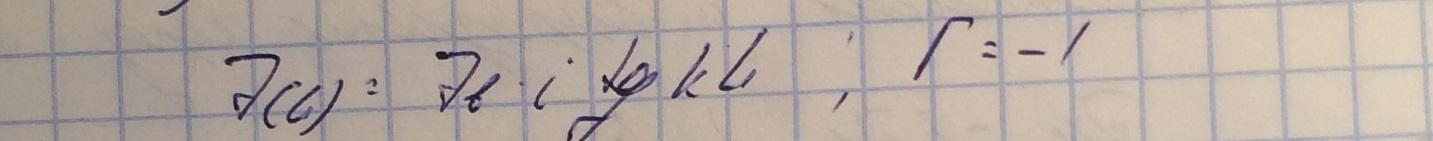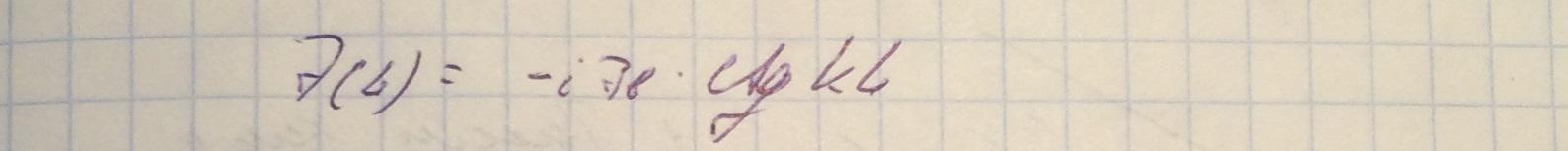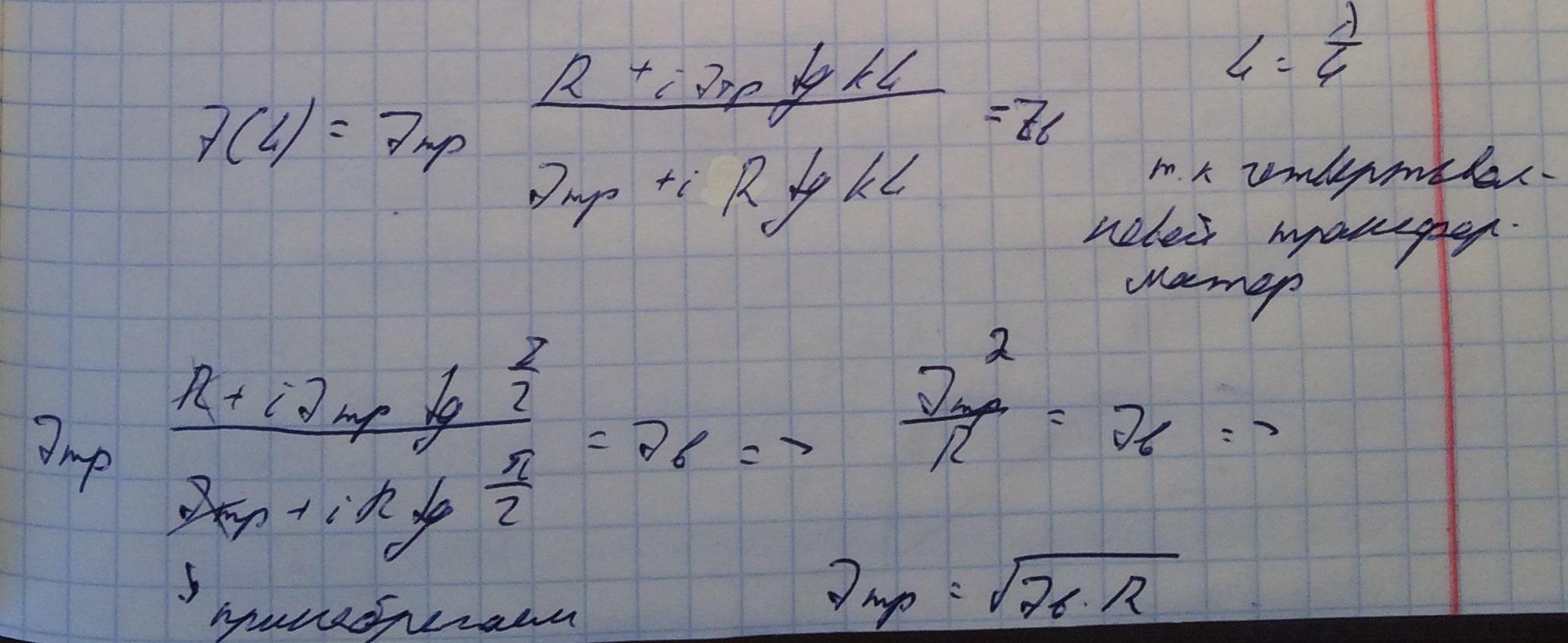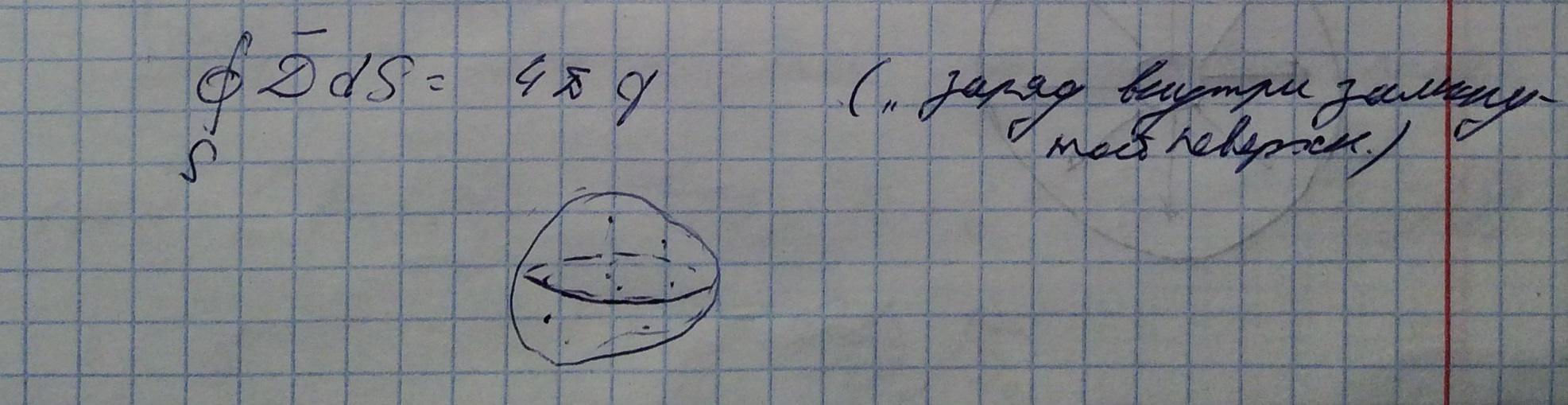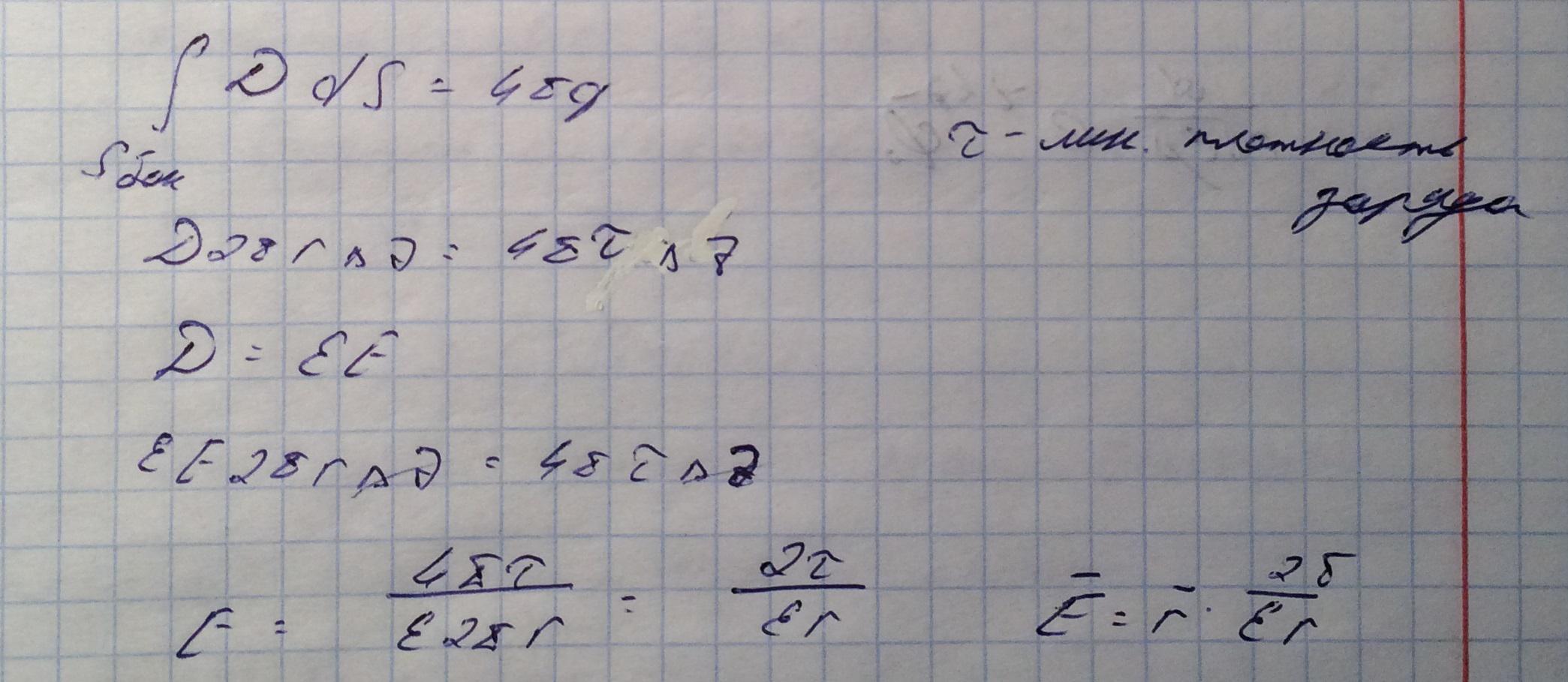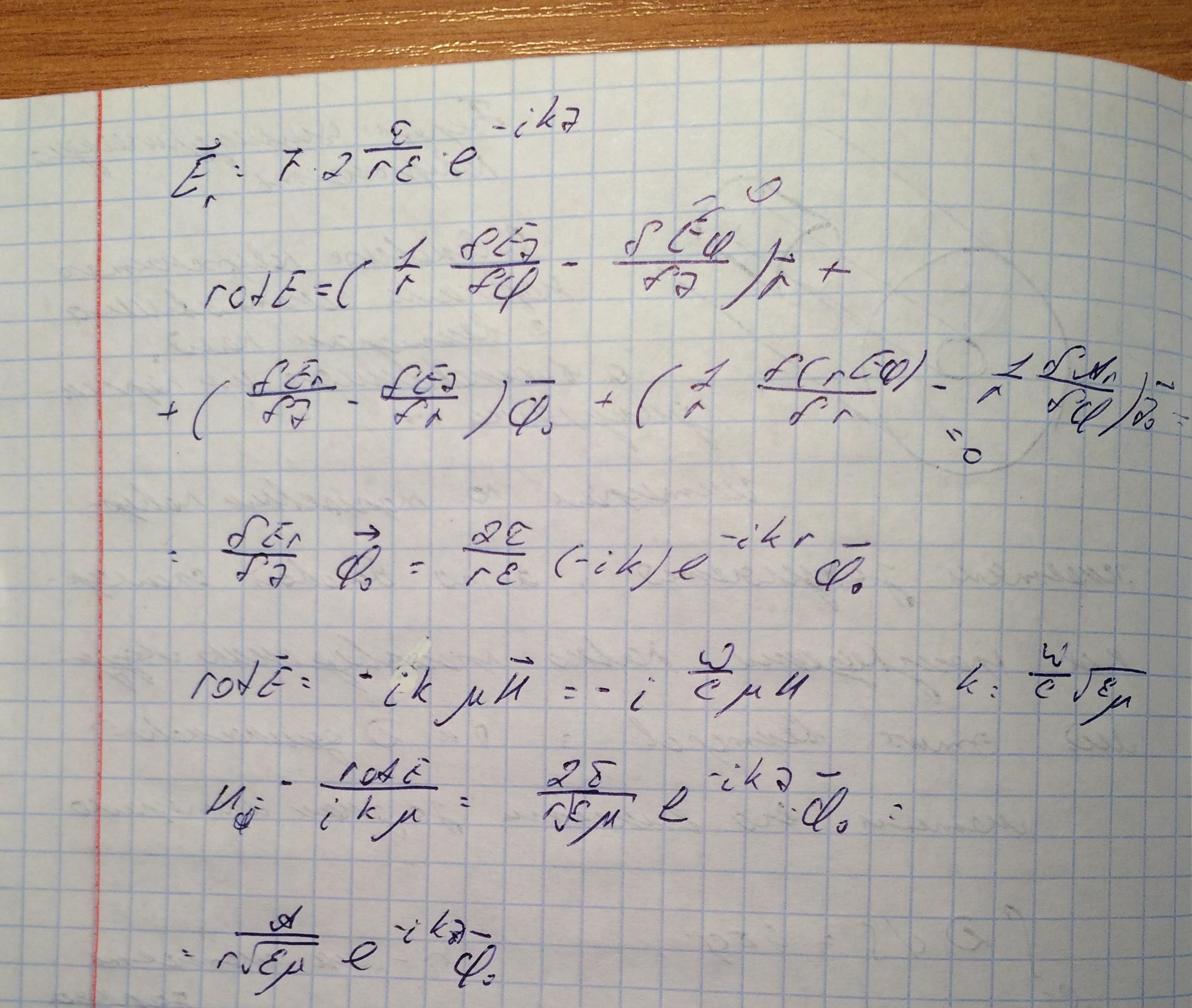Ссылка на оглавление.

ТЕМ  волны

Рассмотрим предельный случай ТМ волны (см. Уравнения полей в волноводе).

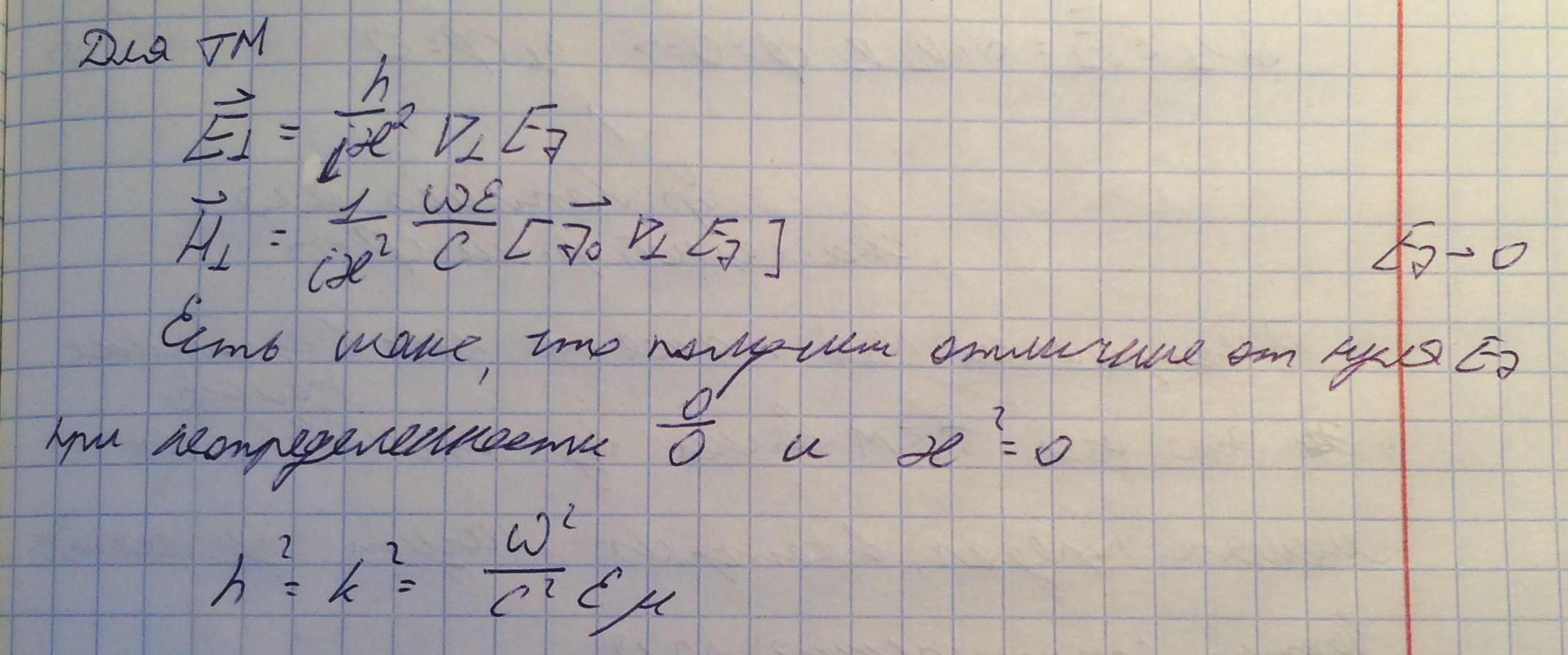
Если такие волны существуют, то это волны без дисперсии, то есть есть возможность передавать сигналы без искажений. Фазовые и групповые скорости будут такие же как и в свободном пространстве. Тоесть спектр на входе волновода равен спектру на выходе волновода.
Сделаем замену переменных:

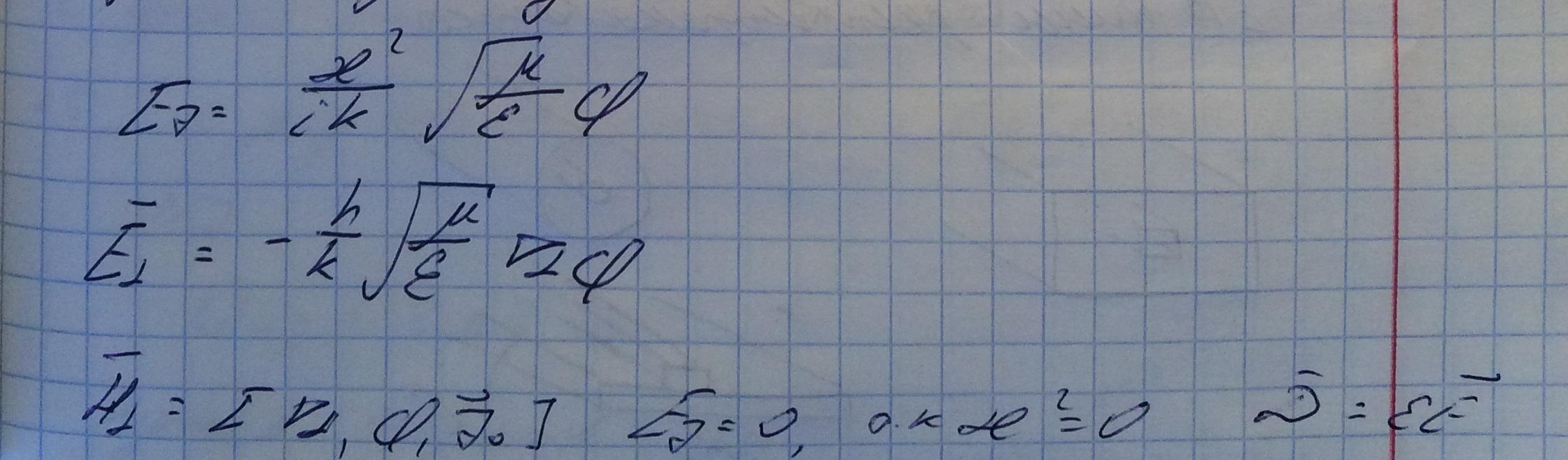
Из уравнения Максвелла без источника:

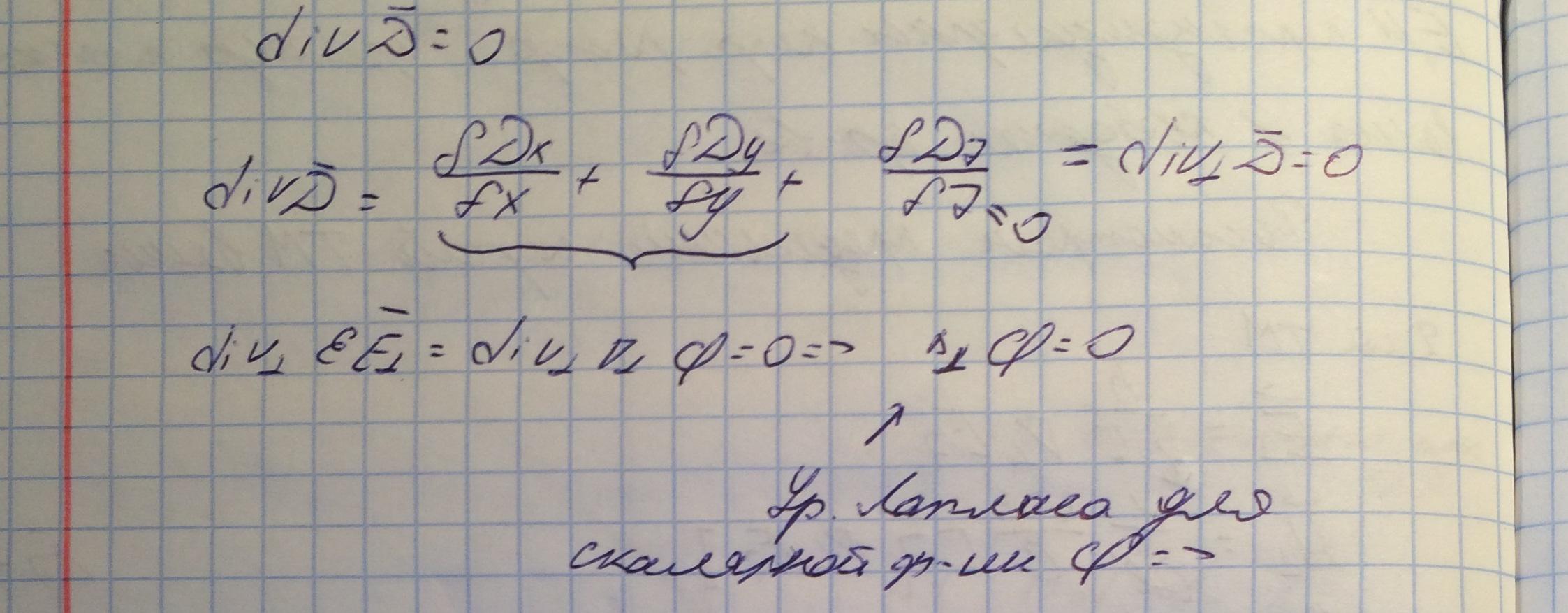
Получили, что электрическое поле данной волны такое же как и в статике.
Это означает, что TEM волны возможны только в тех линиях передач, в которых могут существовать статические поля. При этом структура поля совпадает со структурой поля в статике, так как статическое поле не зависит от продольной компоненты.
ТЕМ волны распространяются в следующих структурах:

Погонная емкость и индуктивность коаксиального волновода.

Рассмотрим  вспомогательные задачи:
Исследуем коаксиальный волновод и найдем его погонную емкость и погонную индуктивность. При этом берем статические поля.

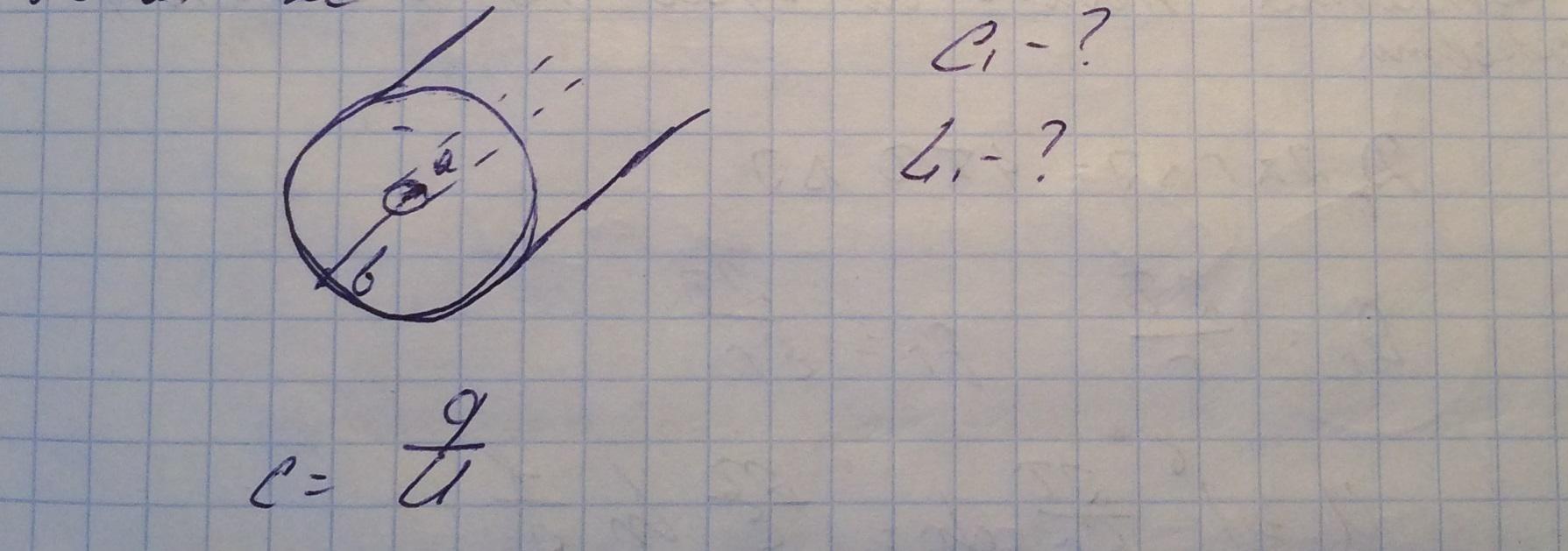
Разместим на центральном проводнике заряд с линейной плотностью и исследуем участок волновода элементарной длины.
Значение для заряда запишем в следующем виде:

Свяжем величины заряда и напряжения для этого выберем цилендрическую поверхность, охватывающую центральную часть, и воспользуемся теоремой Гаусса.

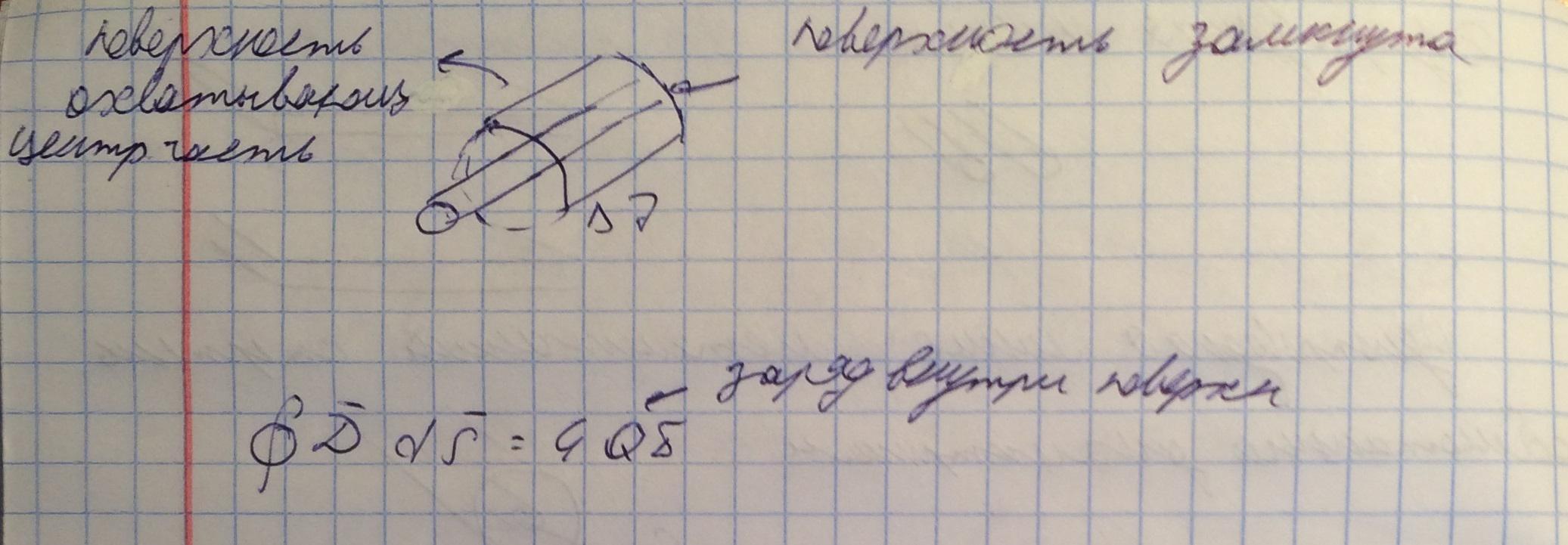
В данном волновде электрическое поле радиально:

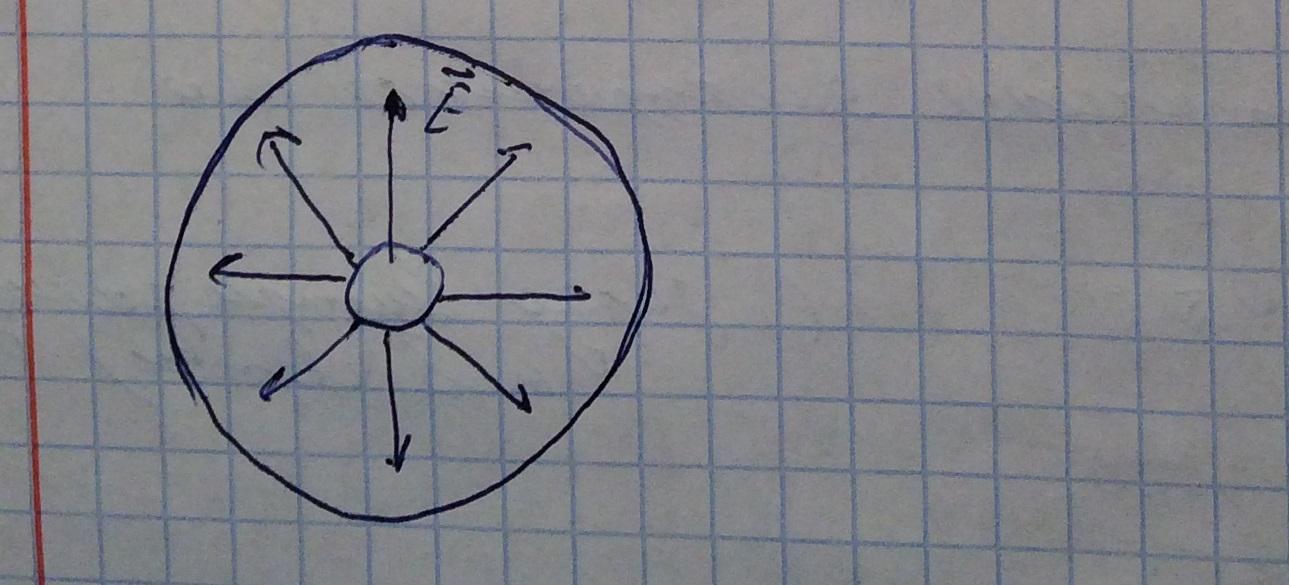
Поэтому исследуем интергал только по боковой поверхности, так как данное электрическое поле касательно к торцевым поверхностям.

Получили значение погонной индуктивности волновода через его геометрические размеры и электрическую проницаемость.
Теперь рассчитаем значение погонной индуктивности, используя теорему о циркуляции магнитного поля.

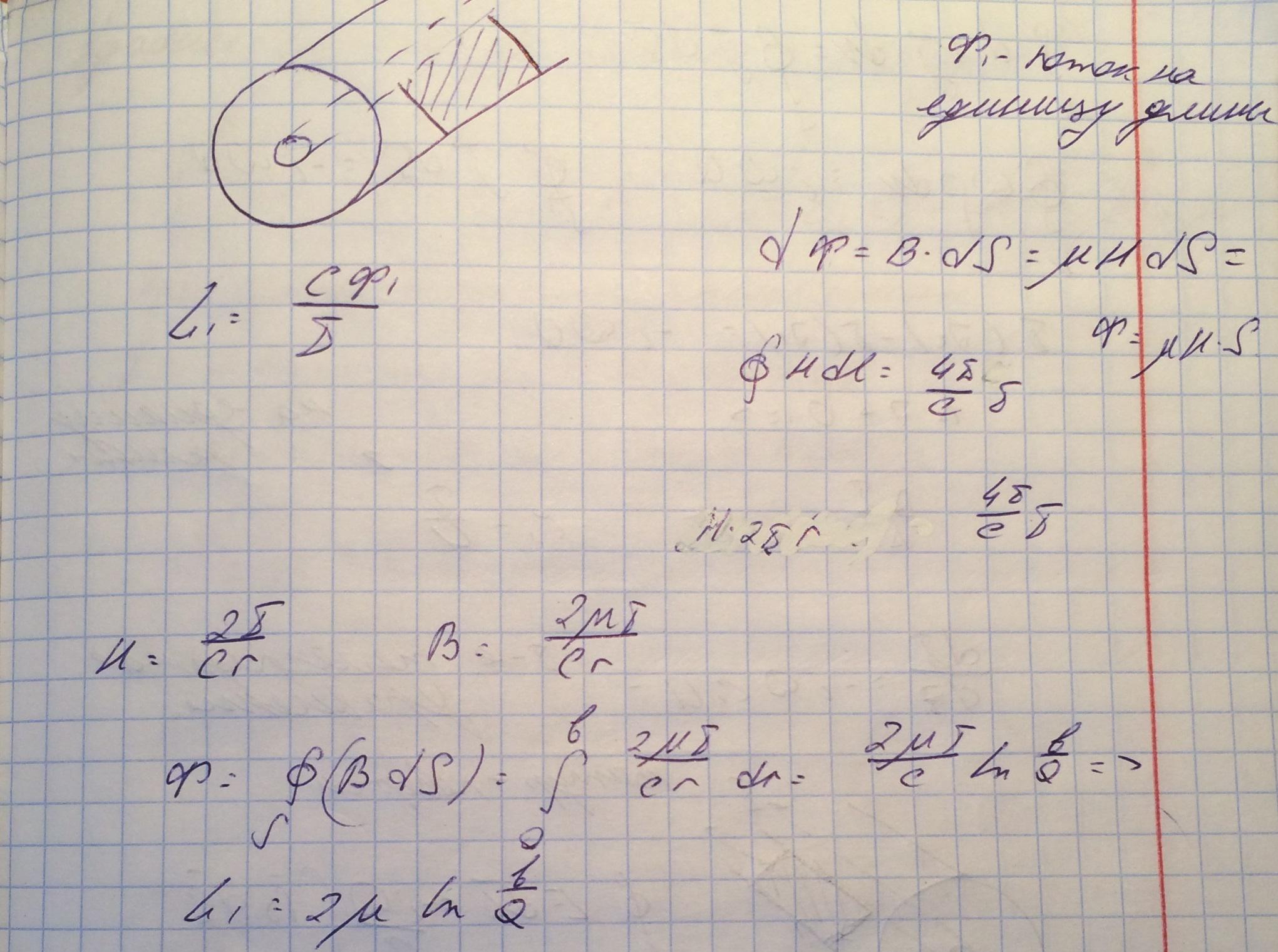
Получили выражение для погонной индуктивности, которая по аналогии с погонной емкостью выражена через геометрические размеры волновода. 

Телеграфные уравнения

Считаем, что погонные параметры совпадают в статике и для TEM волн.
1. Уравнение для токов.
Воспользуемся уравнением непрерывности.


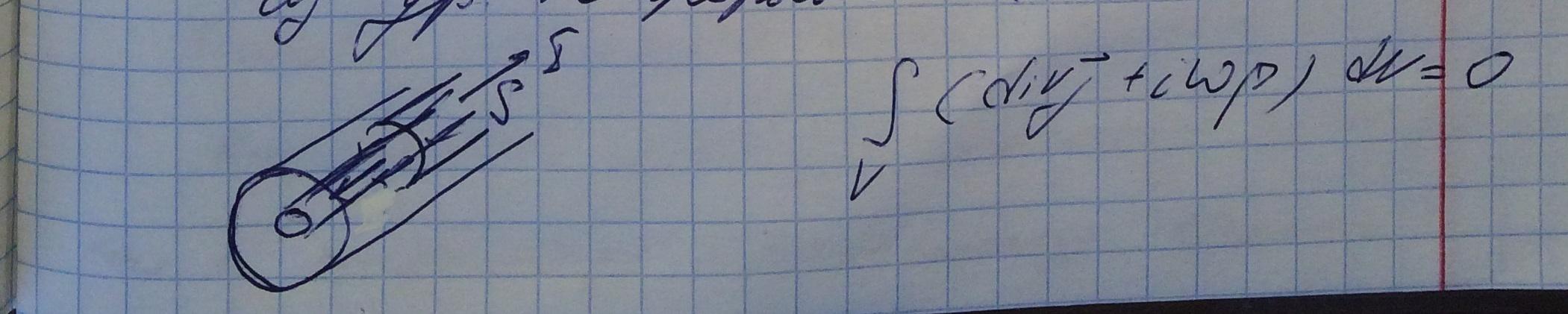
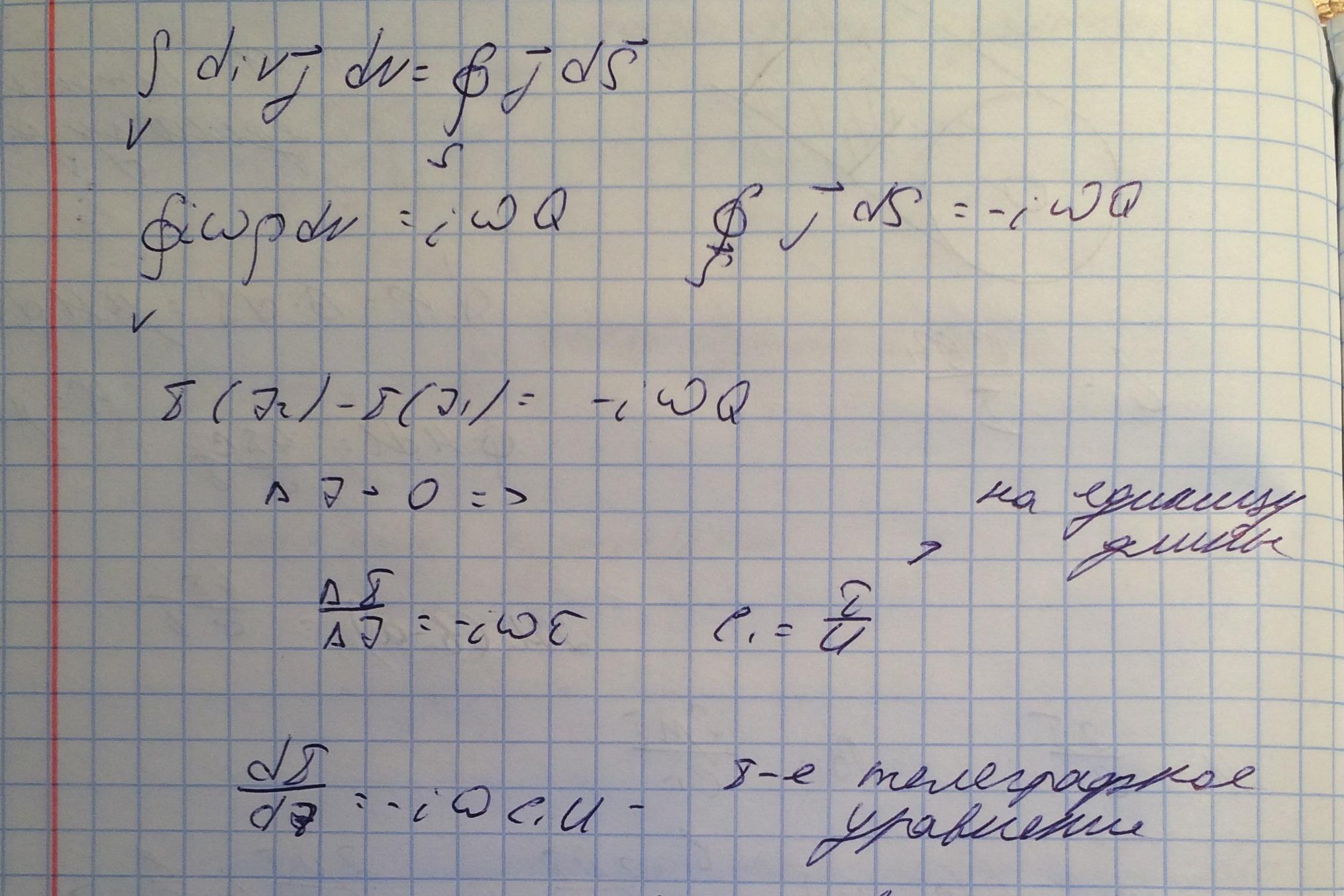
2. Уравнение для напряжений:

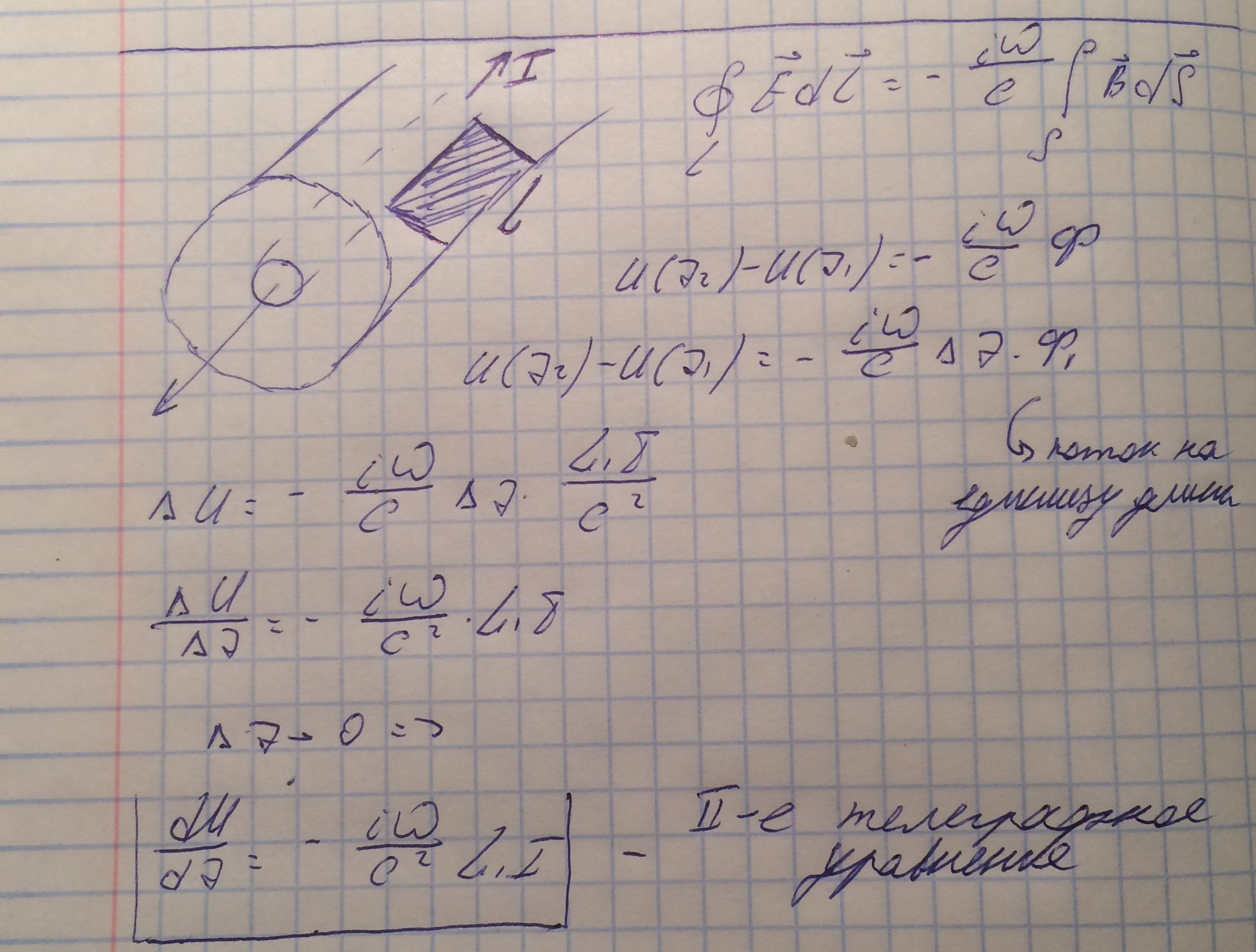
Удобнее из двух уравнений прийти к одному.


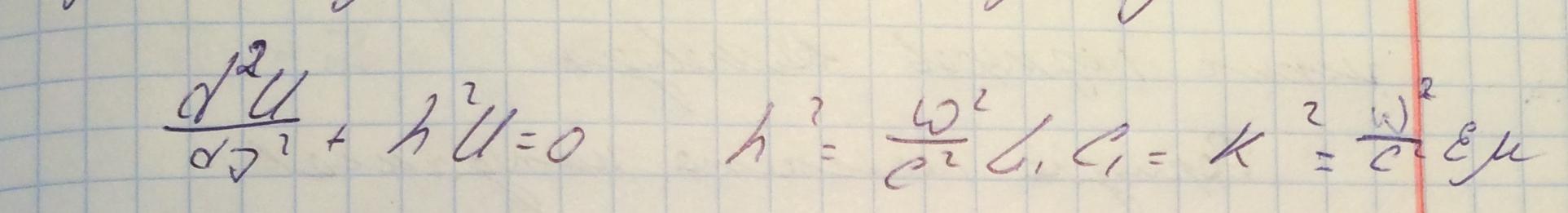
При этом напряжение в данном случае отличается от статического. Введение скалярных величин для токов и напряжений обусловлено удобством в практическом использовании. При этом их значение изменяется только вдоль продольной компоненты z и не зависит от формы траектоии самой линии.
Решение данного уравнения запишем в виде:

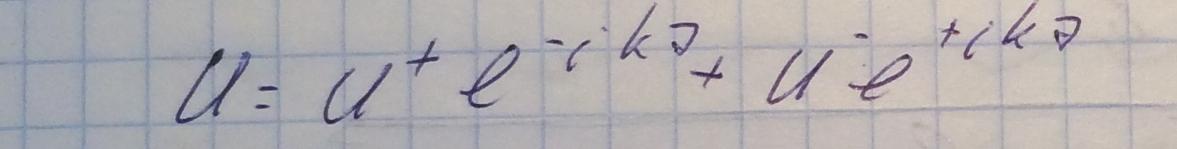
Знак "+" отвечает за компоненту напряжения, направленную вдоль оси z, а знак "-" отвечает за компоненту напряжения, направленную против оси z. Будем работать с волной направленной в положительном направлении z. 
Тогда значения напряжения и тока равны:

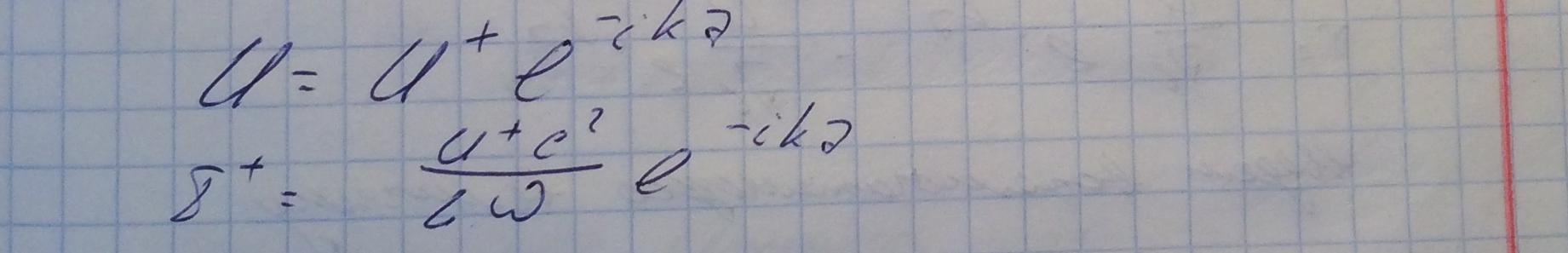
Введем понятие волнового импеданса в бегущей волне:

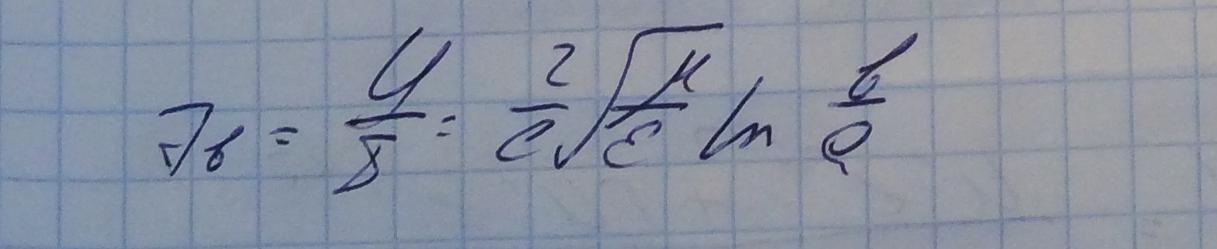
Заметим, что данное выражение зависит от геометрических размеров линии.

Подробная информация о телеграфных уравнениях доступна в интернет ресурсе Wikipedia.

Формула пересчета импедансов 

Рассмотрим коаксиальную линию.

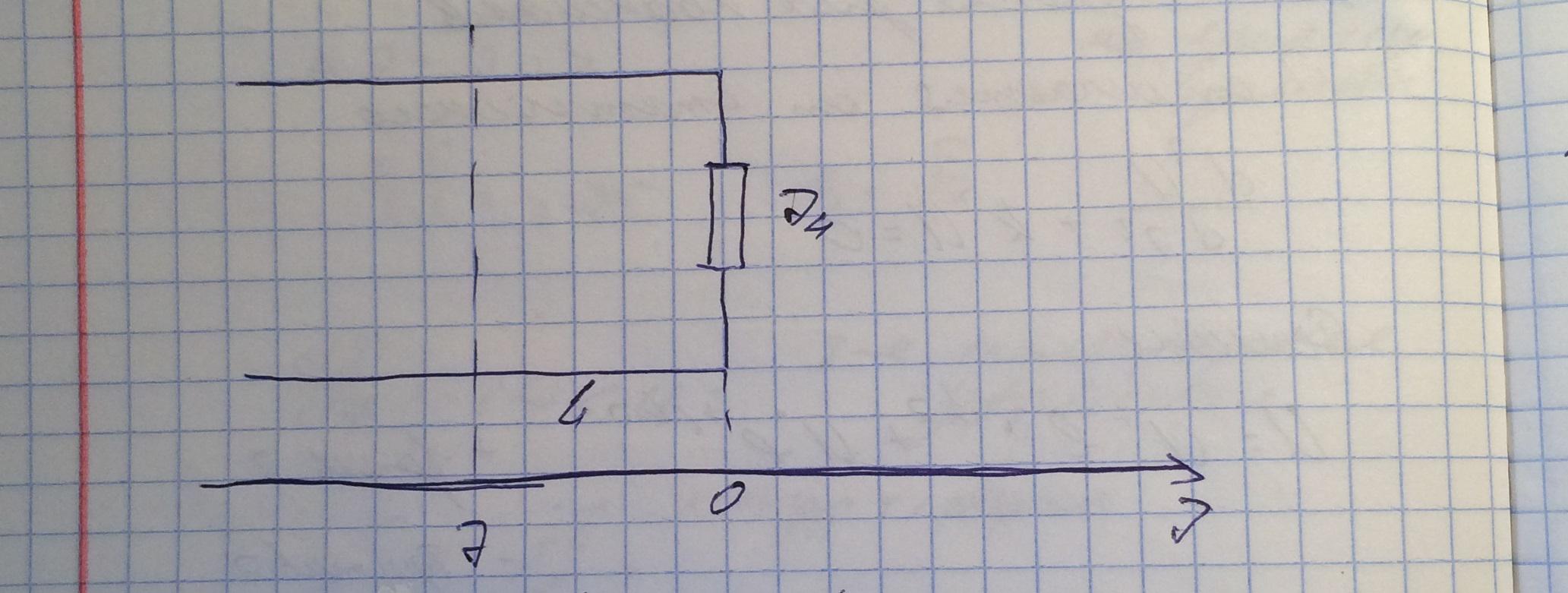
Запишем уравнения для тока и напряжения в ней.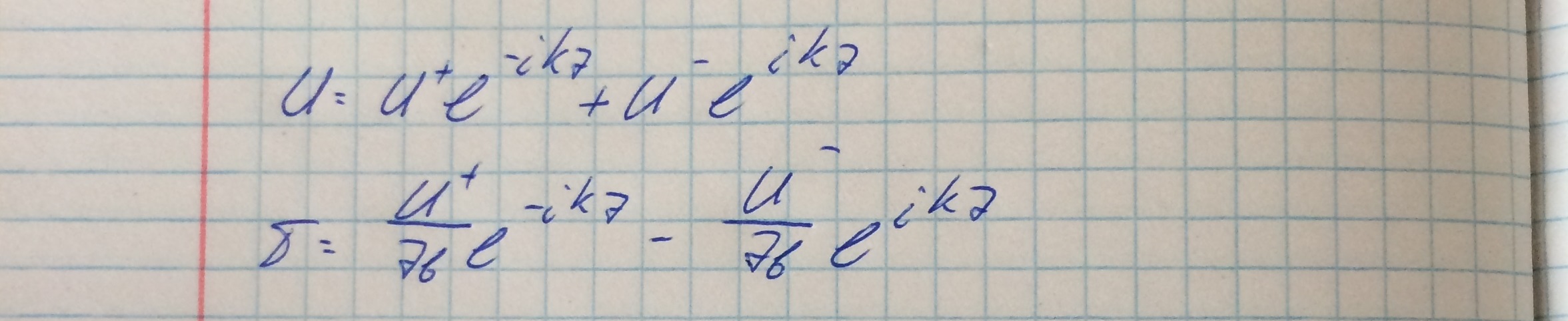

Введем вспомогательную величину, которя называется коэффициентом отражения в сечении z, равное отношению амплитуды отраженной волны, к амплитуде падающей.

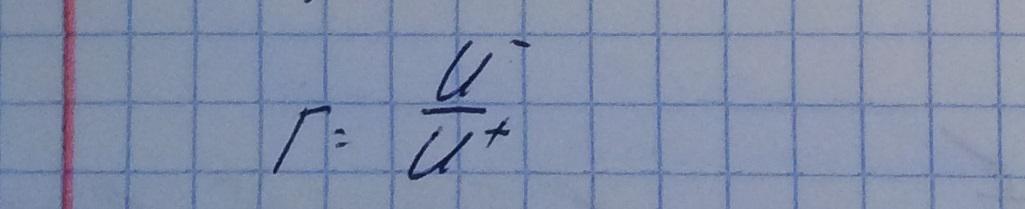
Теперь запишем выражение для импеданса в сечении:

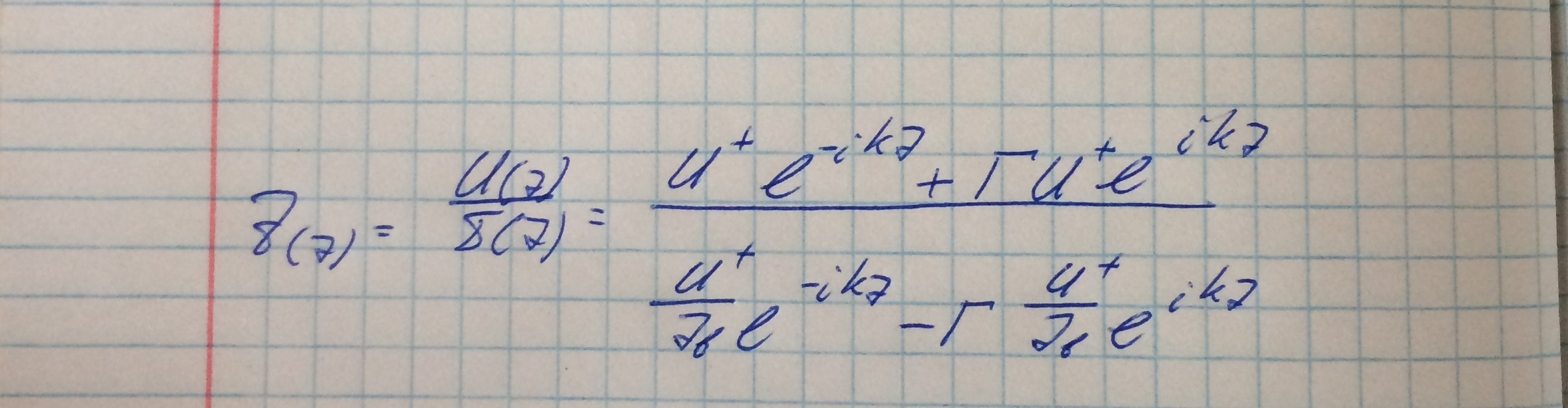
Воспользуемся граничным условием, тоесть то, что импеданс в начале координат равен импедансу нагрузки. Из него выразим коэффициент отражения, которе подставим в значение имеданса в сечении:

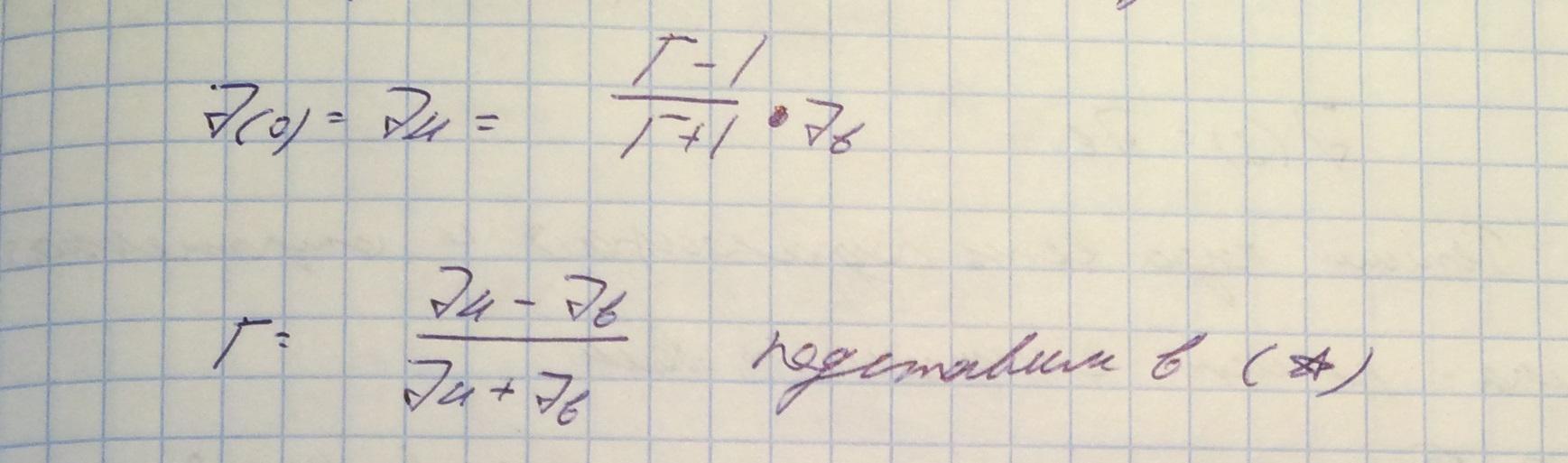
При этом необходимо преобразовать полученное выражение с помощью формулы Эйлера. После чего получим искомую формулу пересчета импедансов.

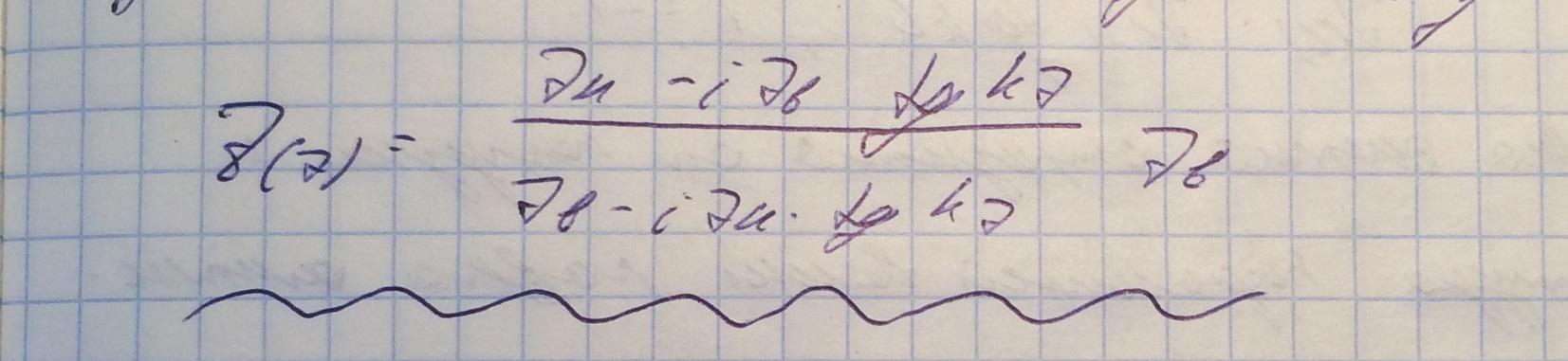
Классическая запись формулы пересчета импедансов имеет вид:

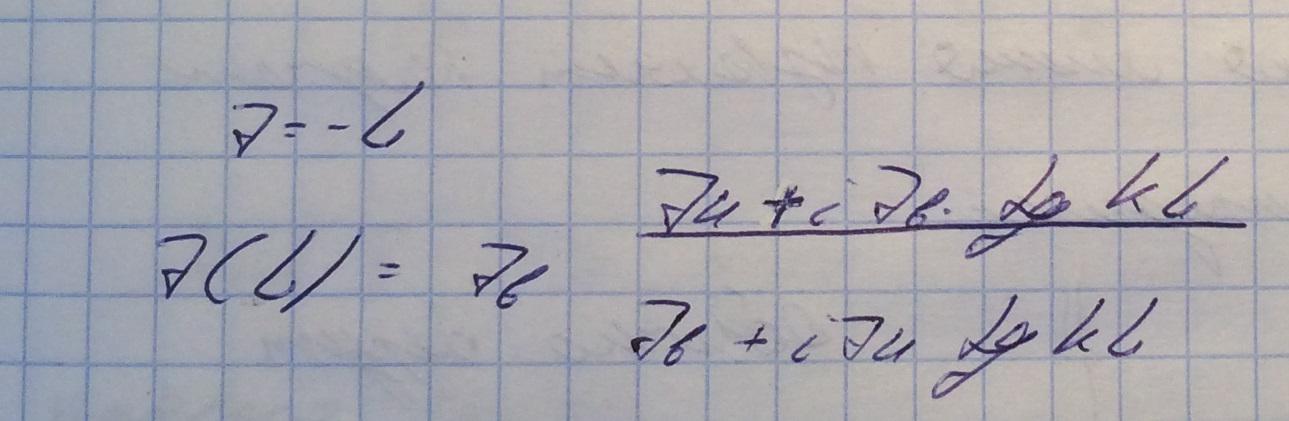
Характерные режимы работы длинной линии.

1. Режим согласования. При данном режиме работы импеданс нагрузки равен волновому сопротивлению, из чего следует что коэффициент отражения равен 0. Значит в данном случае нет встречной волны, которая повышает уровень шума и уменьшает скорость переноса информации. В данном случае  вся энергия поглащается нагрузкой.  Из формулы пересчета импеданса следует:

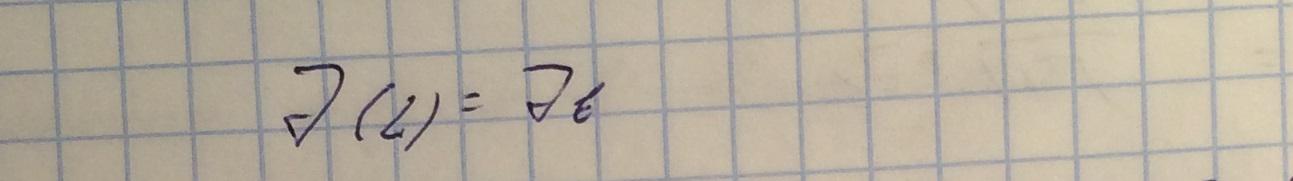
2. Режим короткого замыкания (Случай когда линия закорочена). При данном режиме работы импеданс нагрузки равен нулю, соответственно коэффициент отражения равен минус единице, а из формулы пересчета импедансов следует:

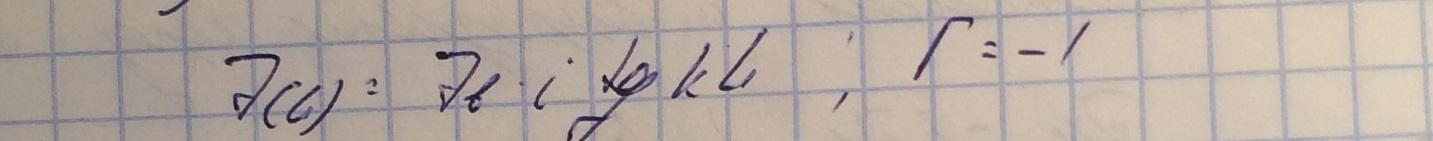
Это означает, что вся энергия отразится от нагрузки и амплитуда падающей волны равна амплитуде отраженной. Закороченная линия позволяет получать реактивный импеданс, что можно проследить по следующему графику:

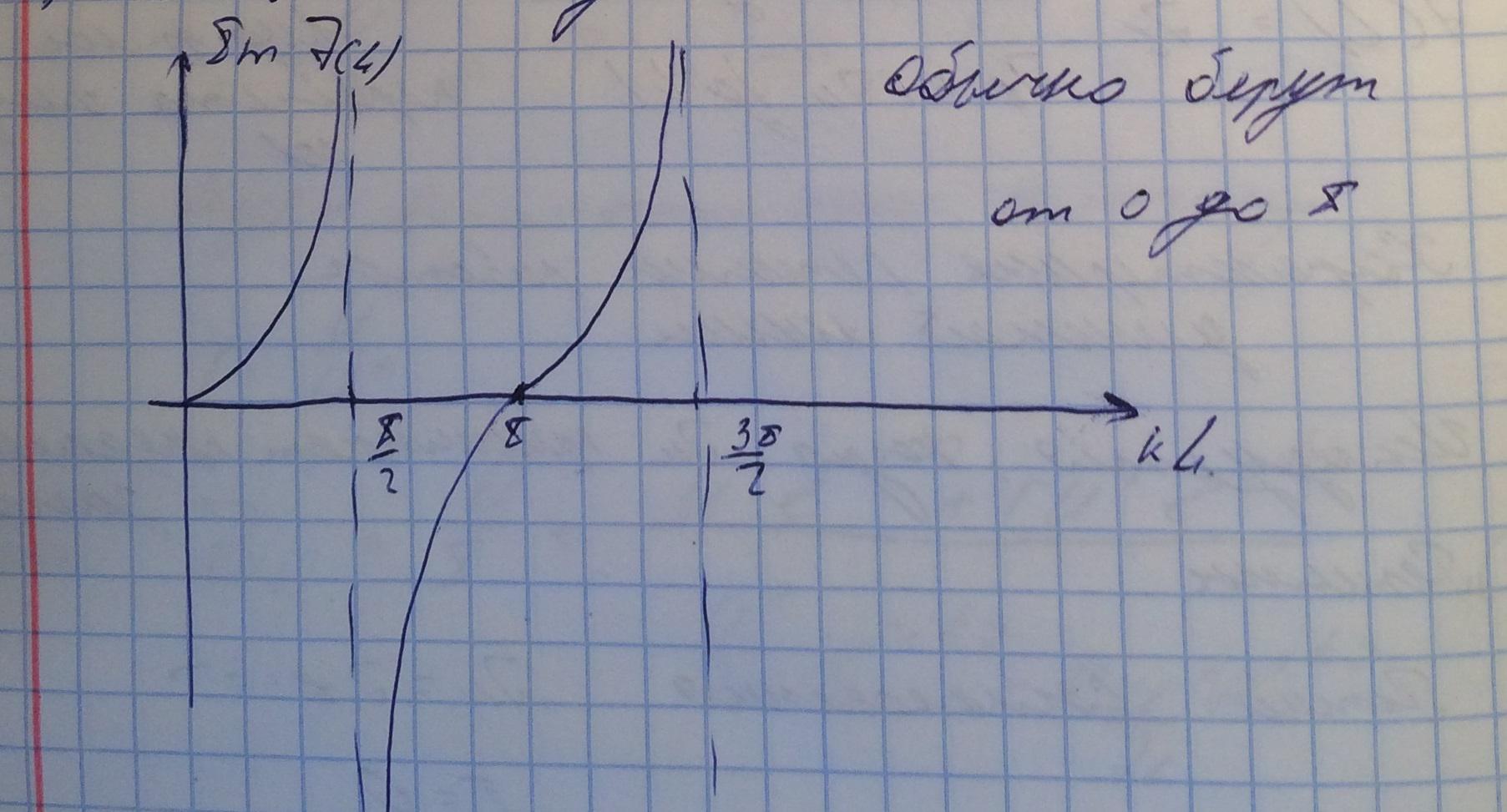
Часть графика, находящаяся выше нуля отвечает за индуктивную нагрузку, а та часть что ниже нуля за емкостную.
3. Режим холостого хода. При данном режиме импеданс нагрузки равен бесконечности, соотвественно коэффициент отражения равен единице, а импеданс в сечении по формуле пересчета импедансов равен:

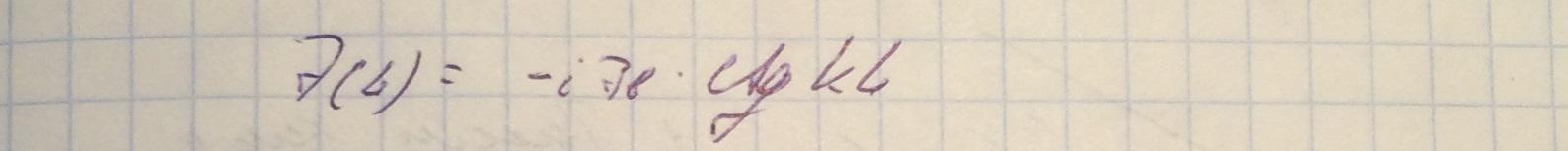
Четвертьволновой трансформатор

Четверть волновой трансформатор представляет собой коаксиальную линию, с одной стороны закороченную нагрузкой, при этом часть линии длины L выполнена из материала, отличного от материала самой линии. 

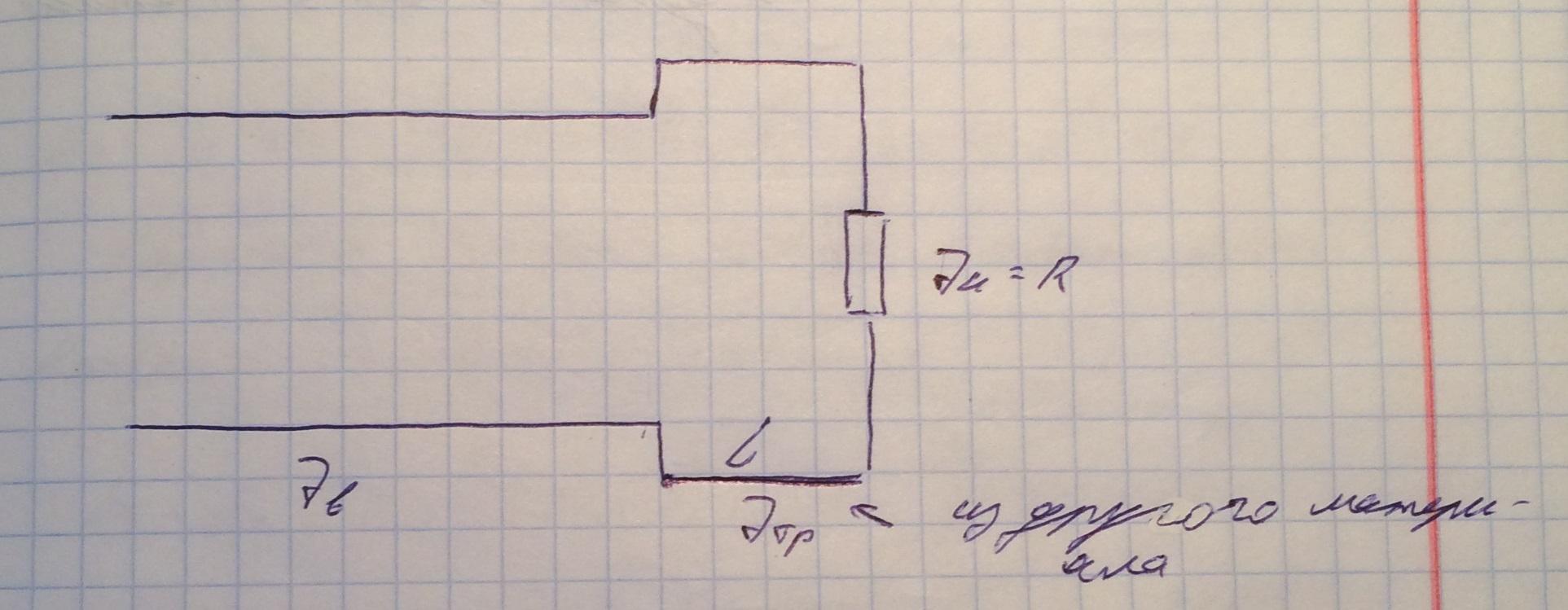
Опредалим теперь импеданс трансформатора и его длину:

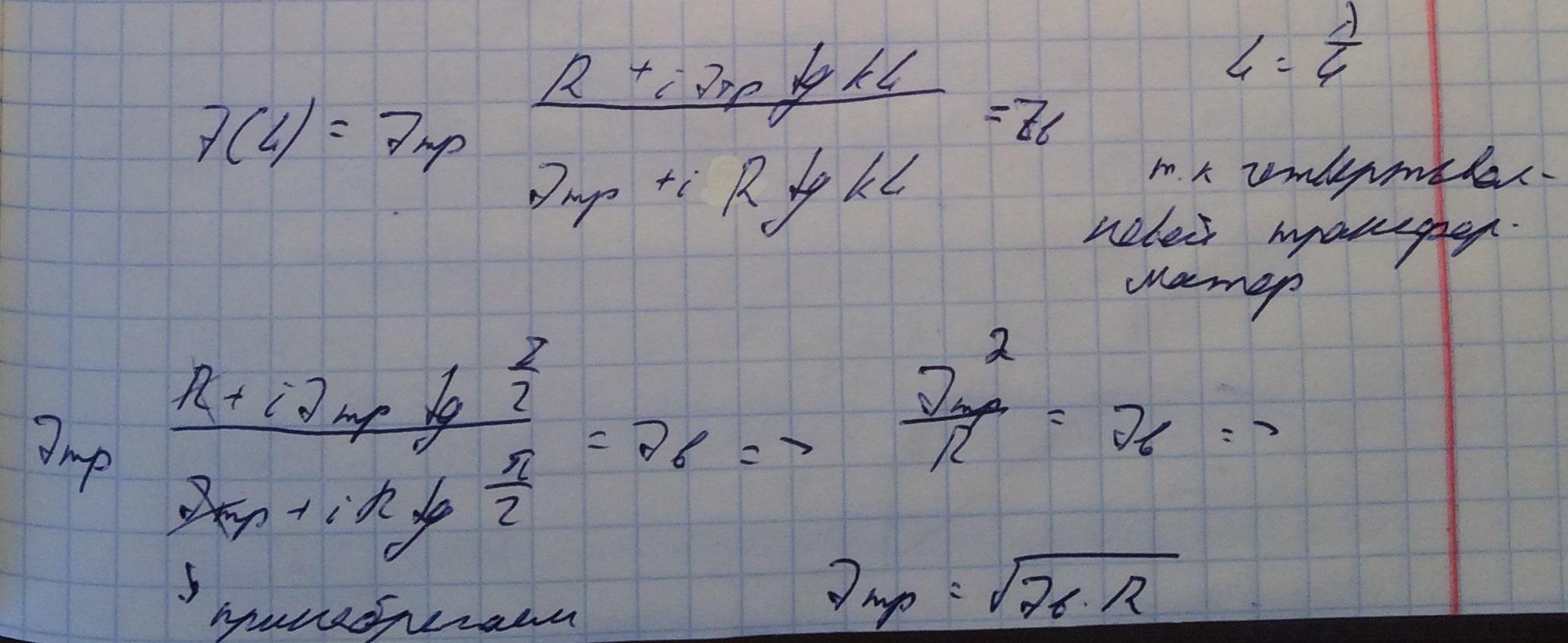
Поля в коаксиальном волноводе

Найдем поля в коаксиальном волноводе, с учетом того, что стенки идеально проводящие. В таокй линии могут существовать разные типы волн, но остановимся на рассмотрении ТЕМ волны, которая распространяется без дисперсии и ее критическая частота очень мала. 
Благодаря симметрии для нахождения полей можем применить уравнения Максвелла в интегральной форме. При этом в статике электрические и магнитные поля не зависят друг от друга, но в динамике это не так.

Найдем статическое электрическое поле.
Воспользуемся теоремой Гаусса:

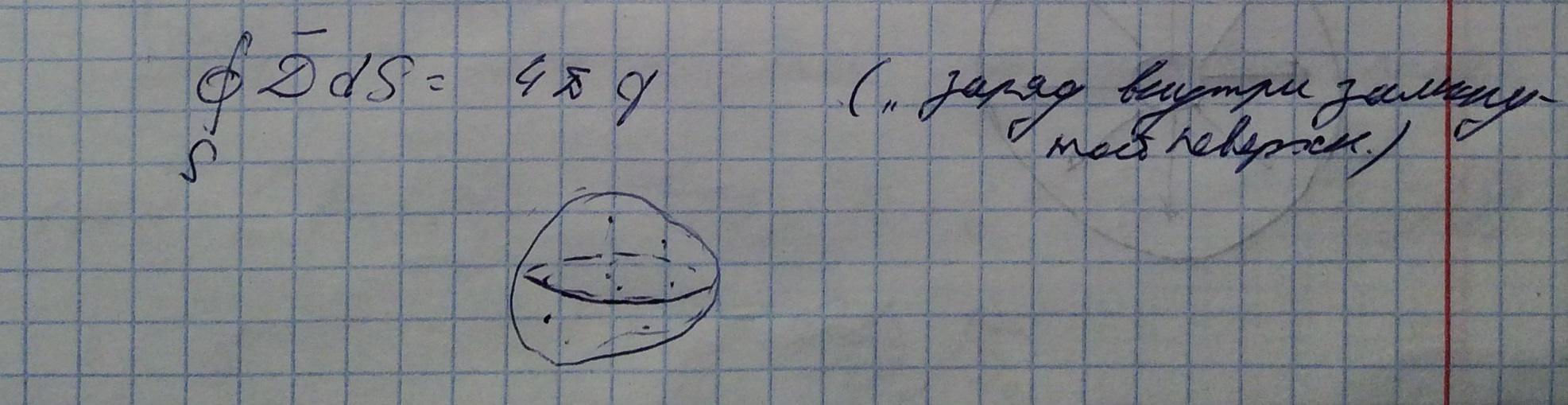
В данном волноводе электрическое поле радиально и симметрично

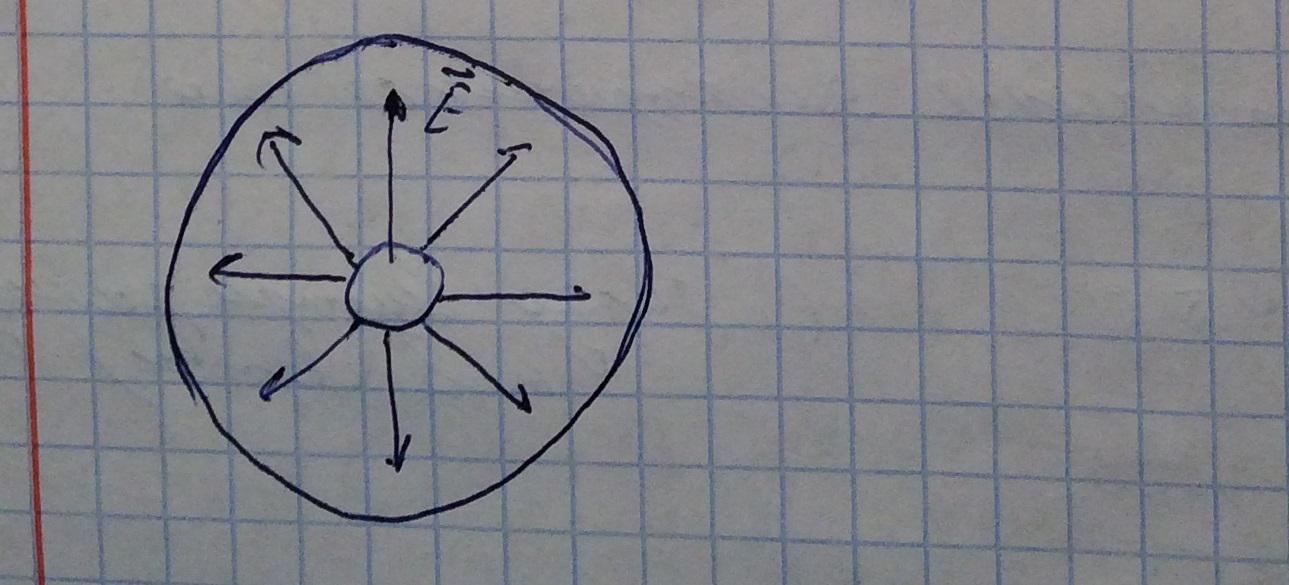
Так как в теореме Гаусса интеграл берется по произвольной замкнутой поверхности, то выберем циллиндричскую поверхность, радиусом r: a<r<b

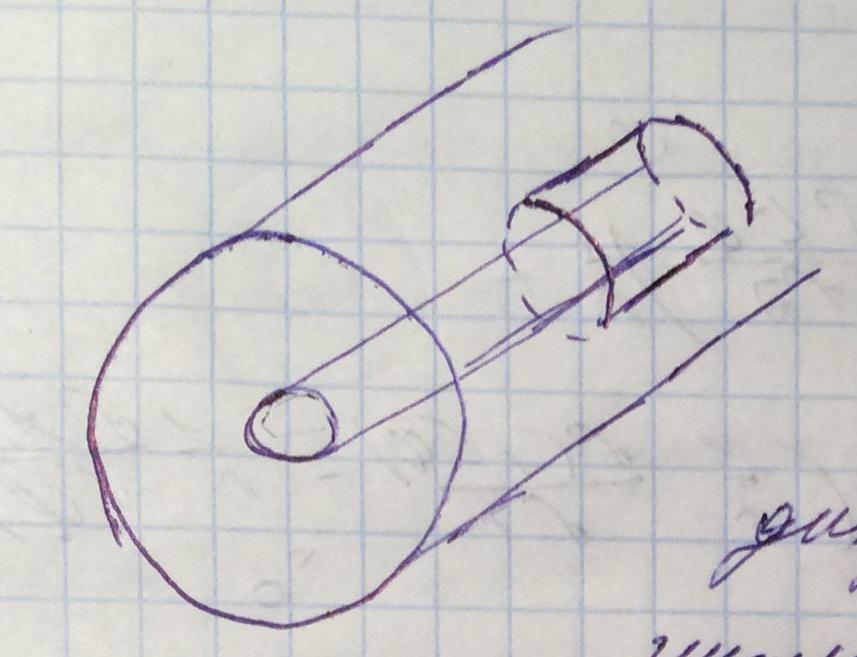
При этом боковые поверхности сонаправлены с векторам поля, а в основания им перпендикулярны, значит интеграл по торцевым поверхностям зануляется, а по боковой поверхности скалярное произведение равно произведению модулей этих вектров, так как величина вектора электрической индукции одинакова (из за симметричнрости поля), значит его можем вынести за знак интеграла в теорема Гаусса. В следствии чего можем выразить вектор электрического поля.

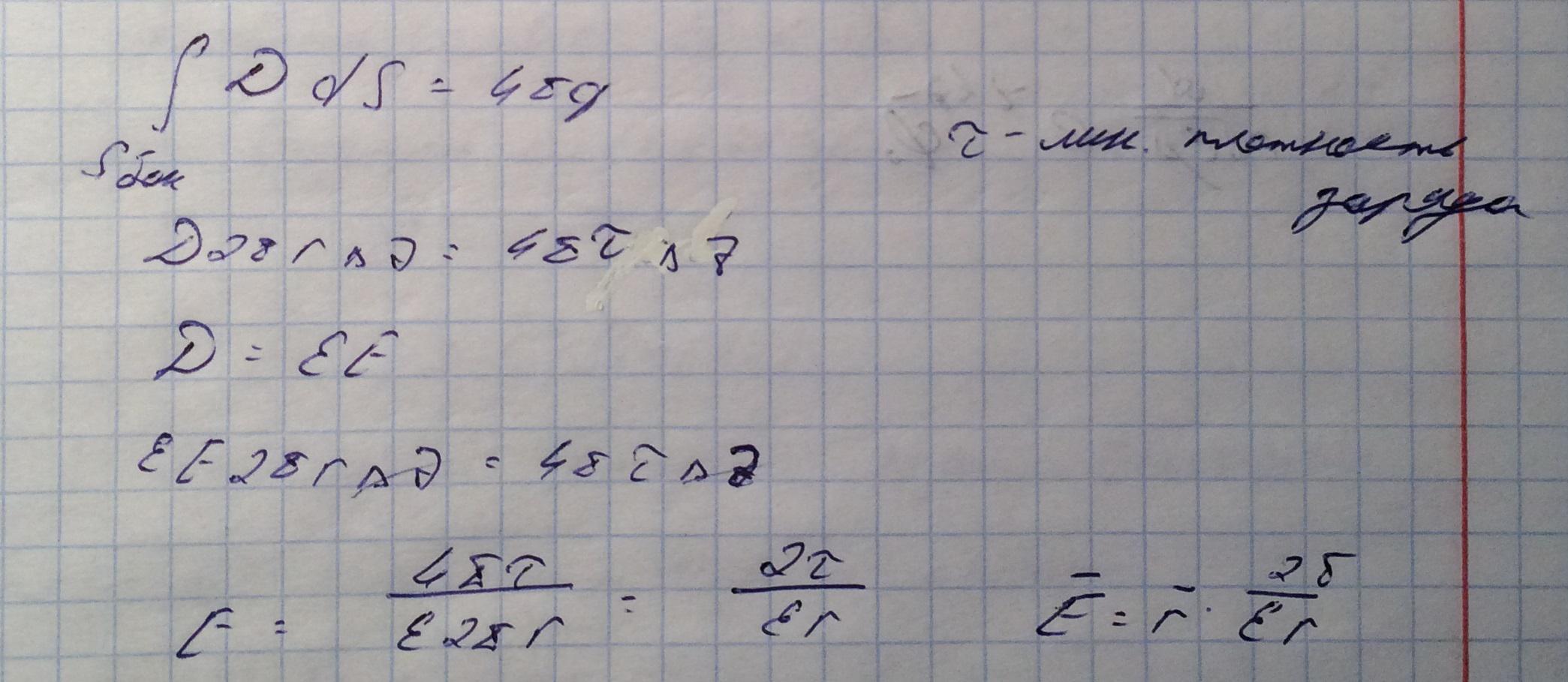
Зная электрическое поле, найдем магнитное поле, раскрывая ротор в полярных координатах.

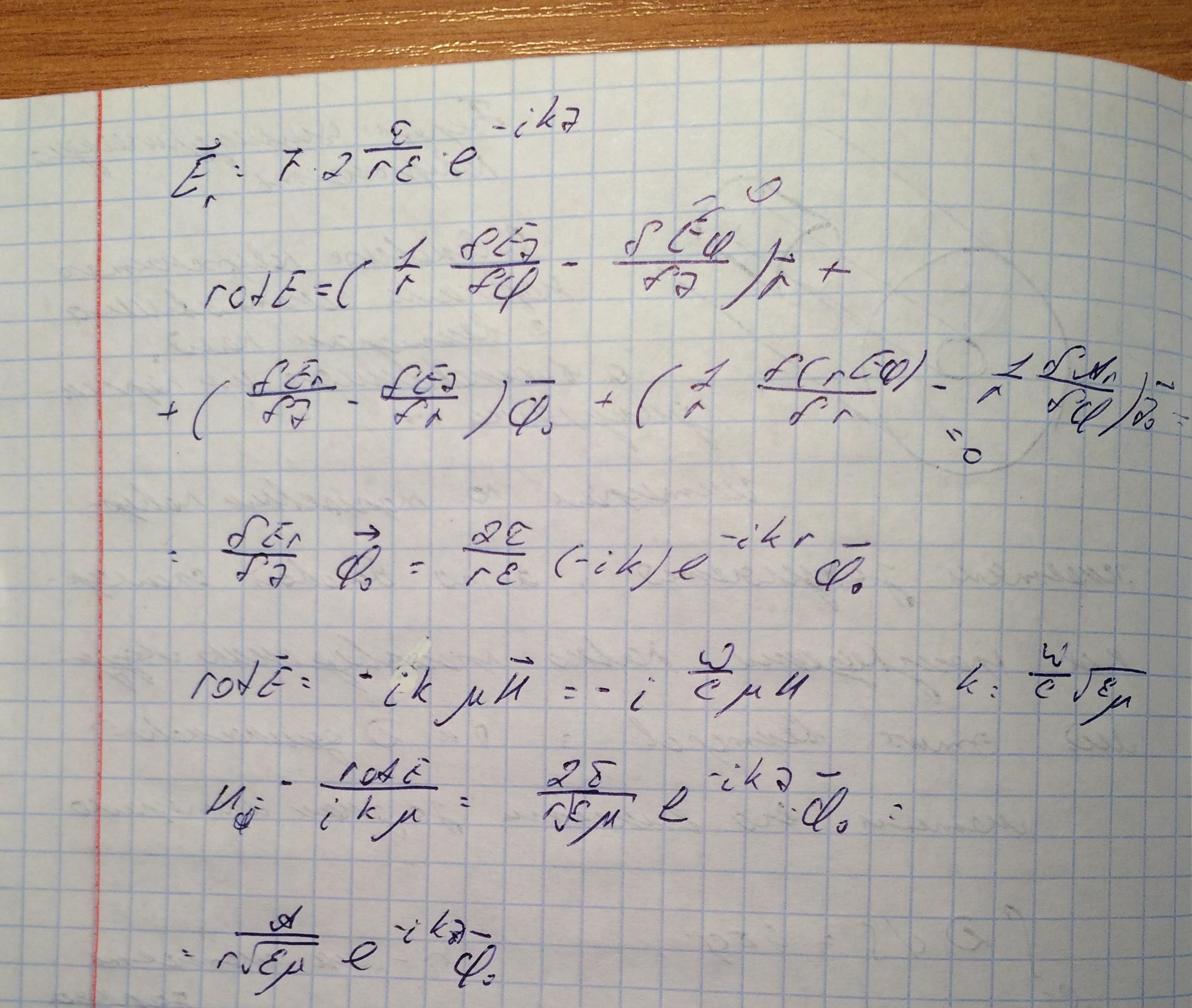
Задача: Дана коаксиальная линия, у которой стенки не идеально проводящие. Определить для нее постоянную затухания. Решение:

Ссылка на оглавление.