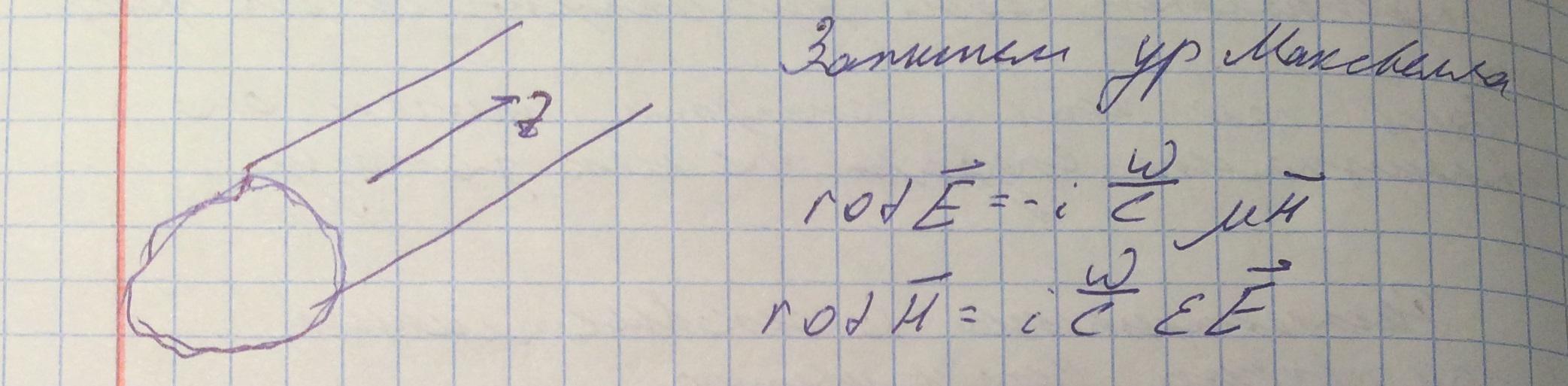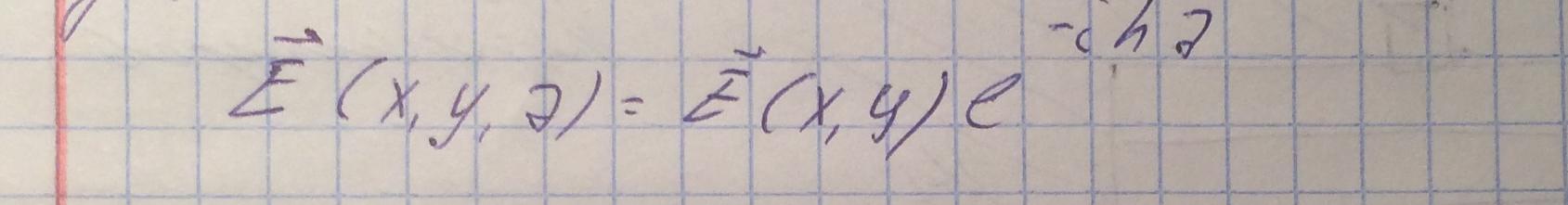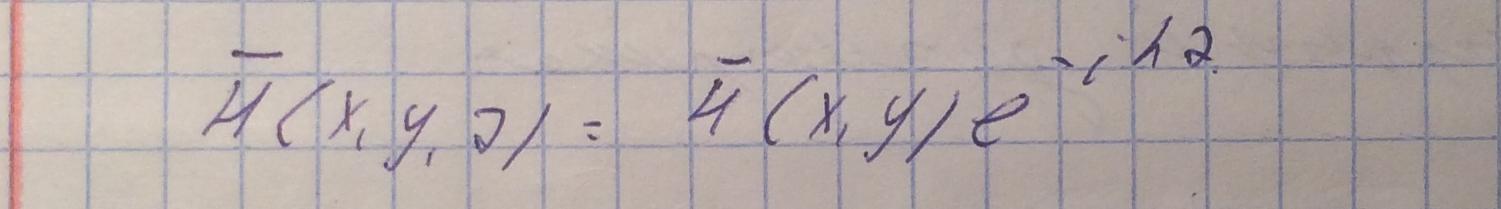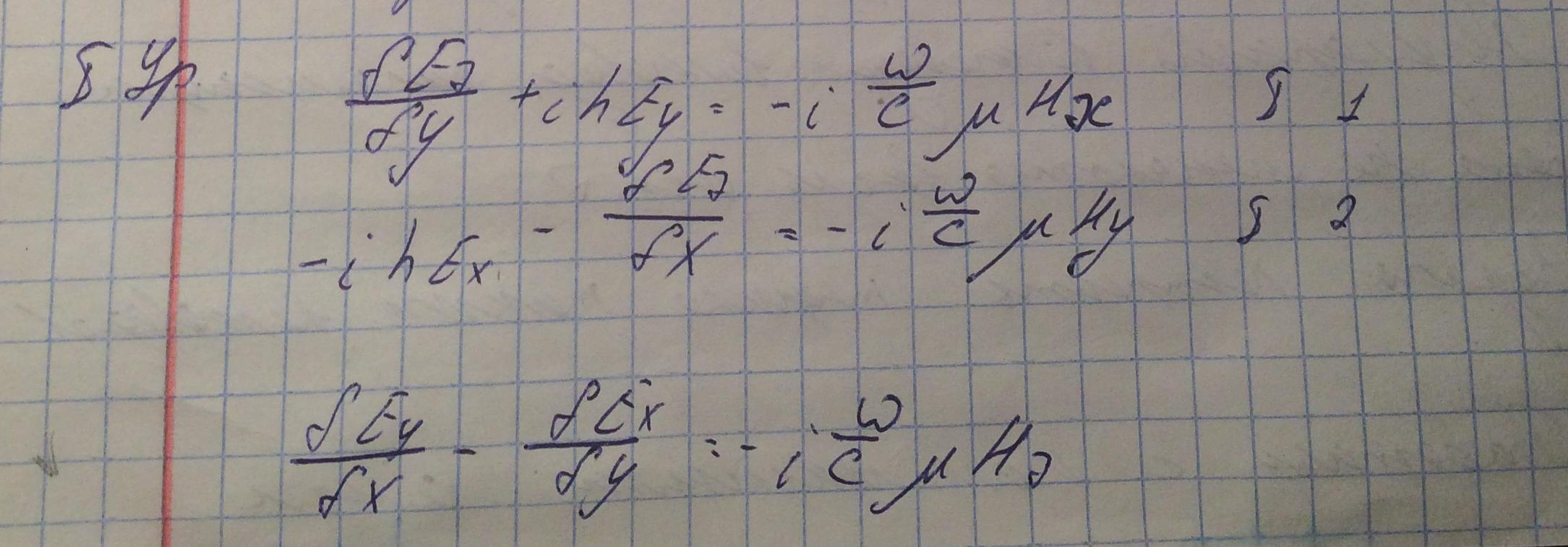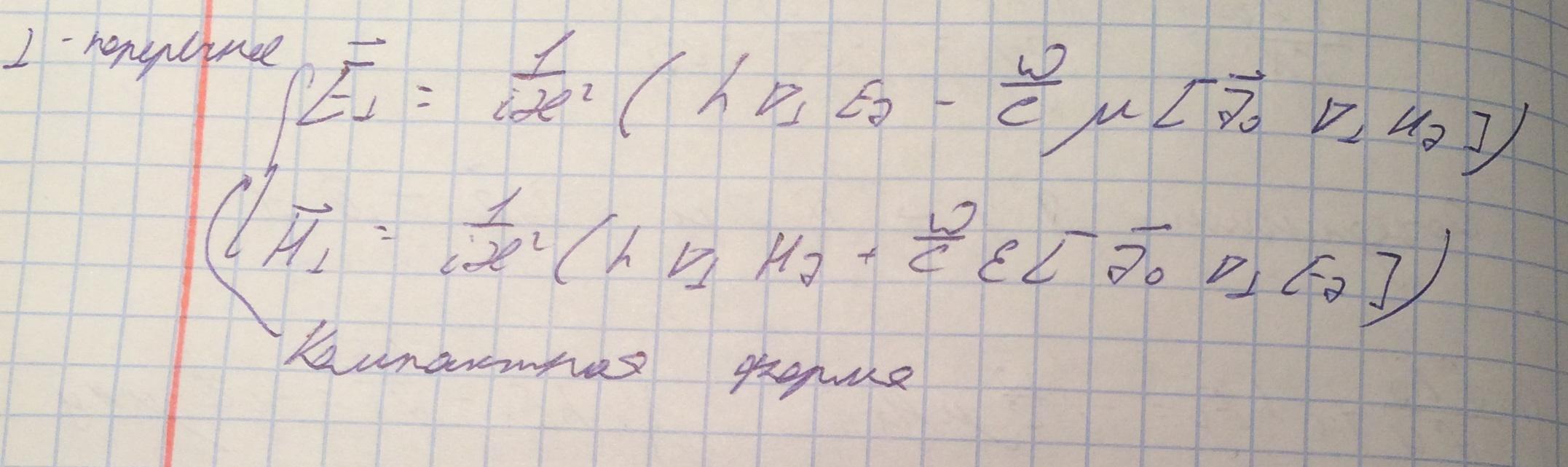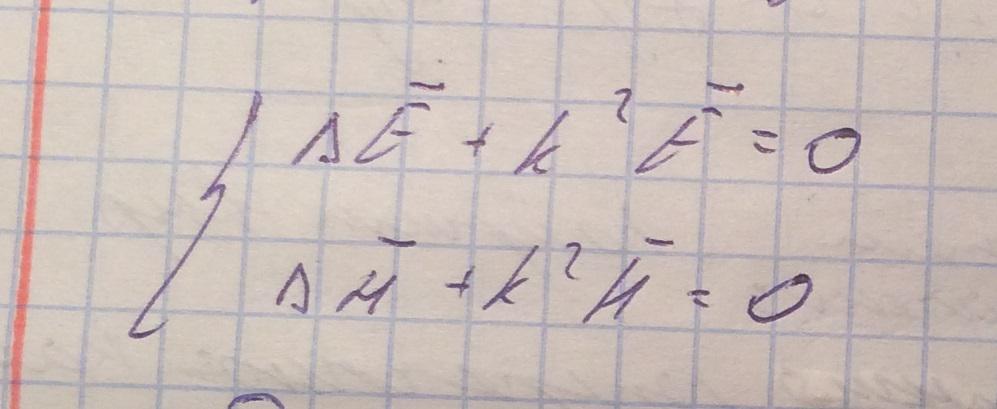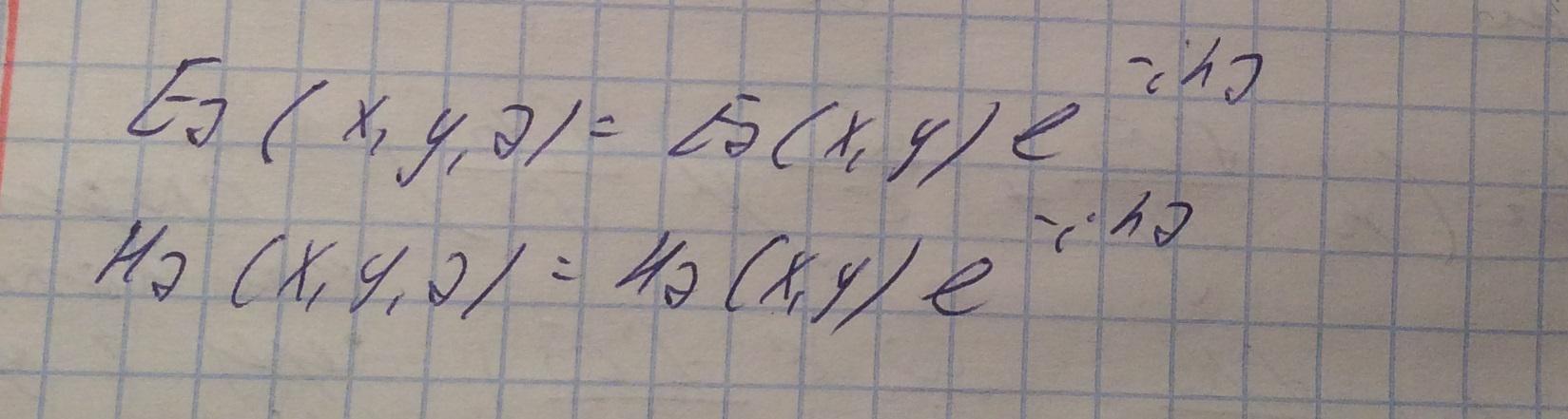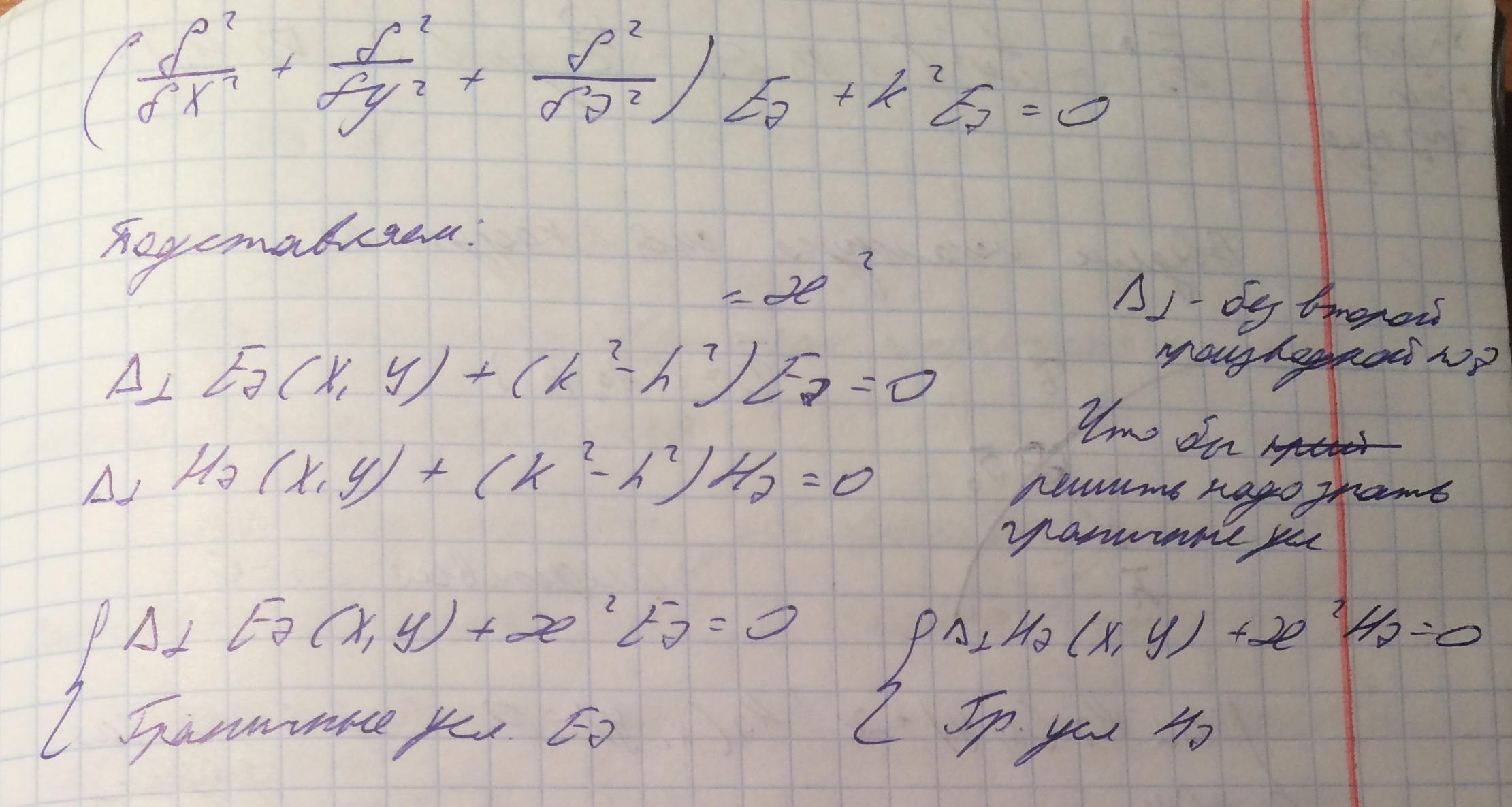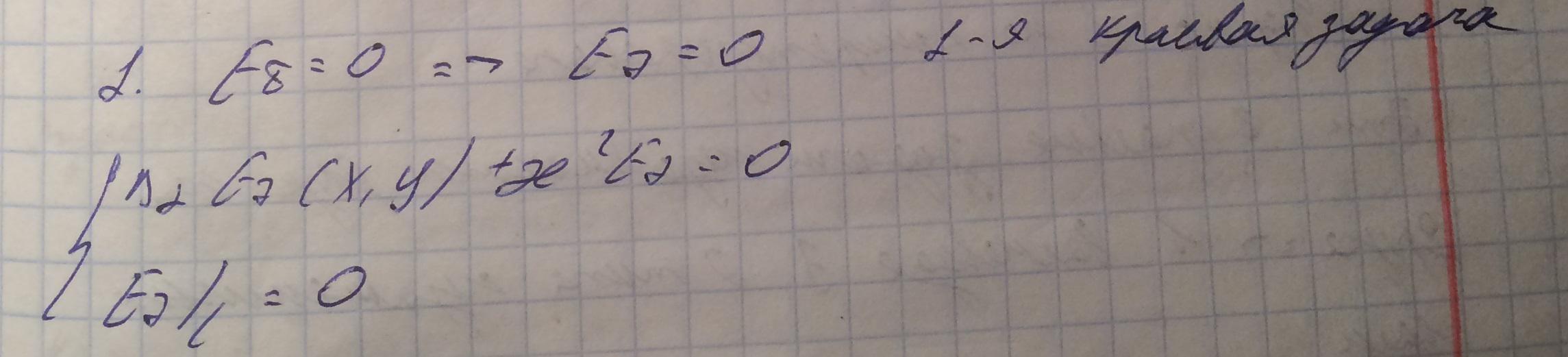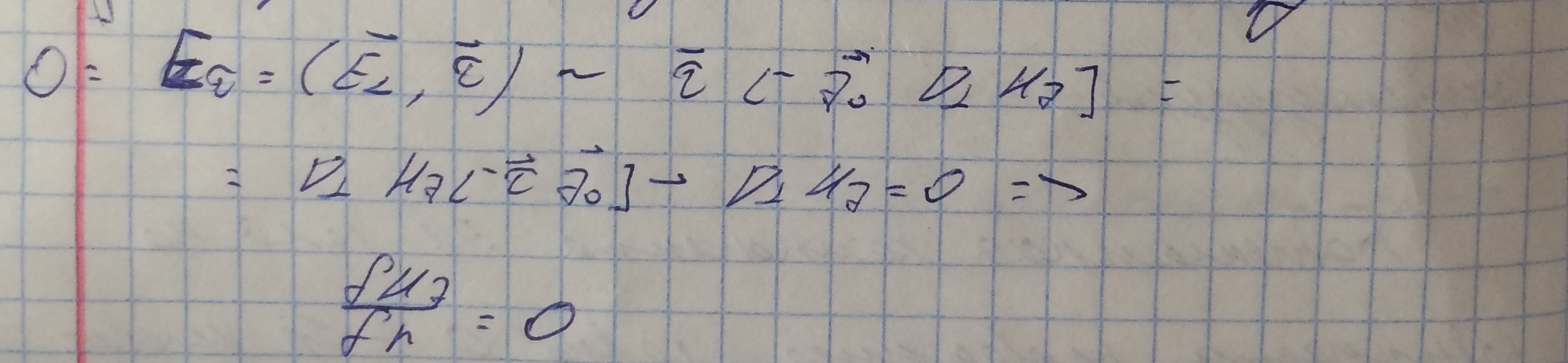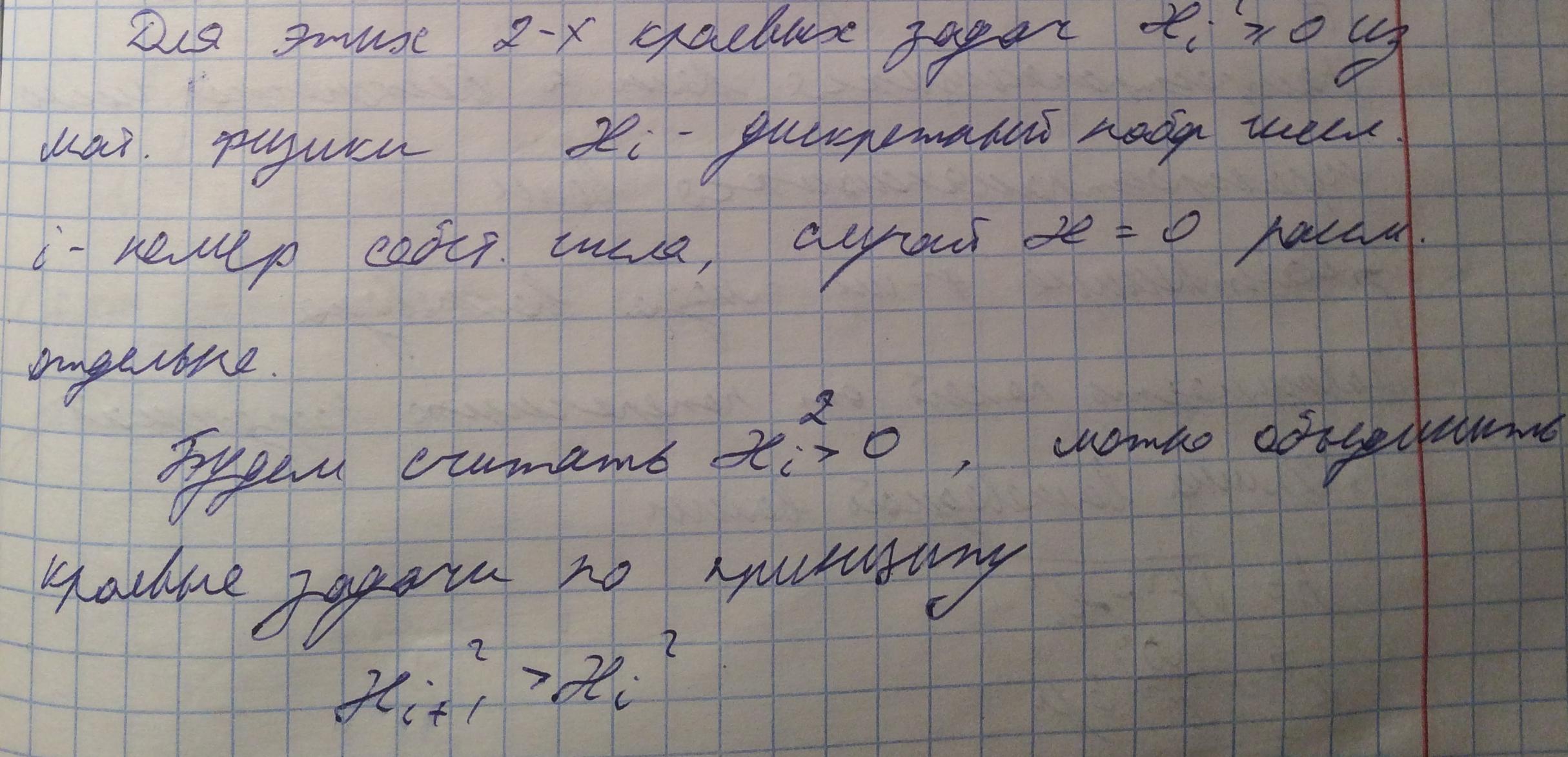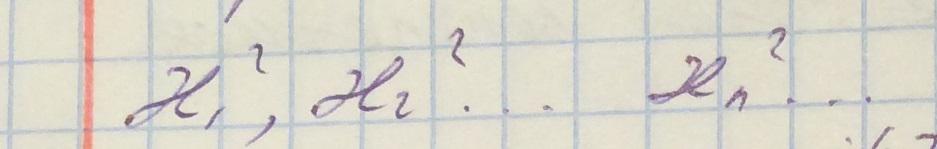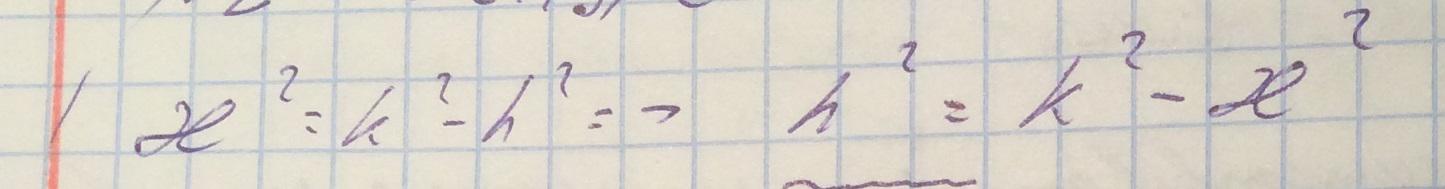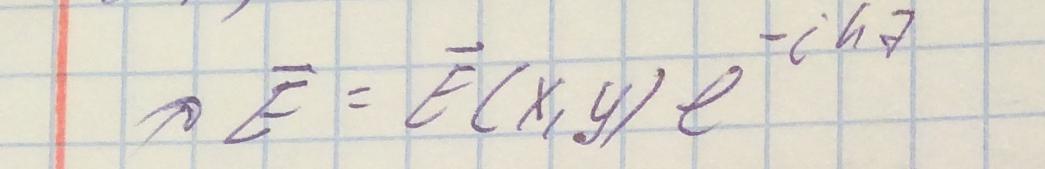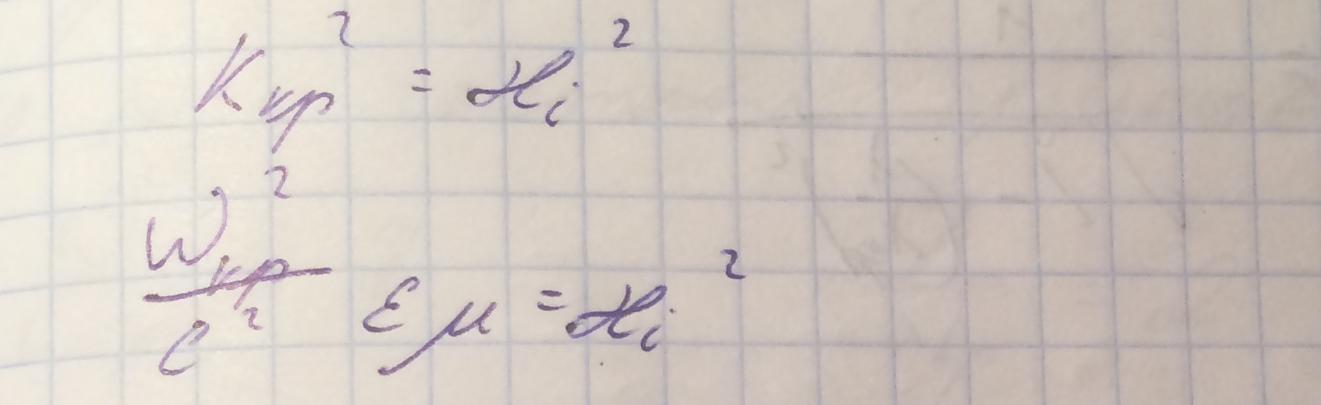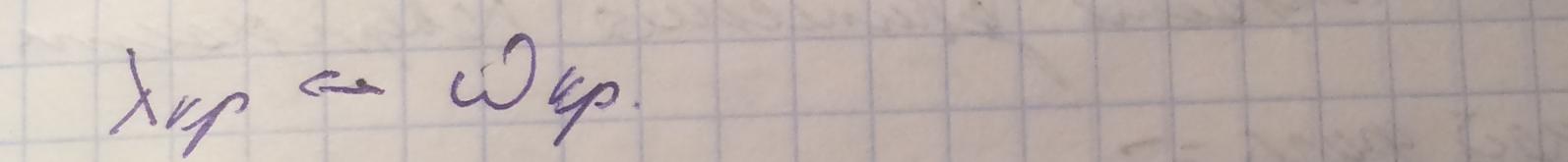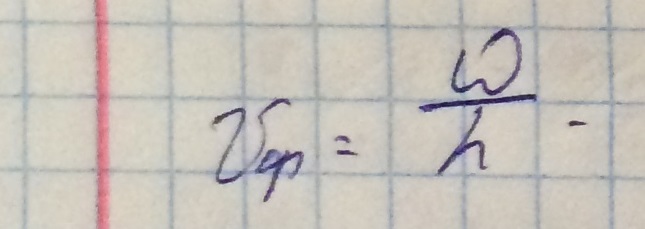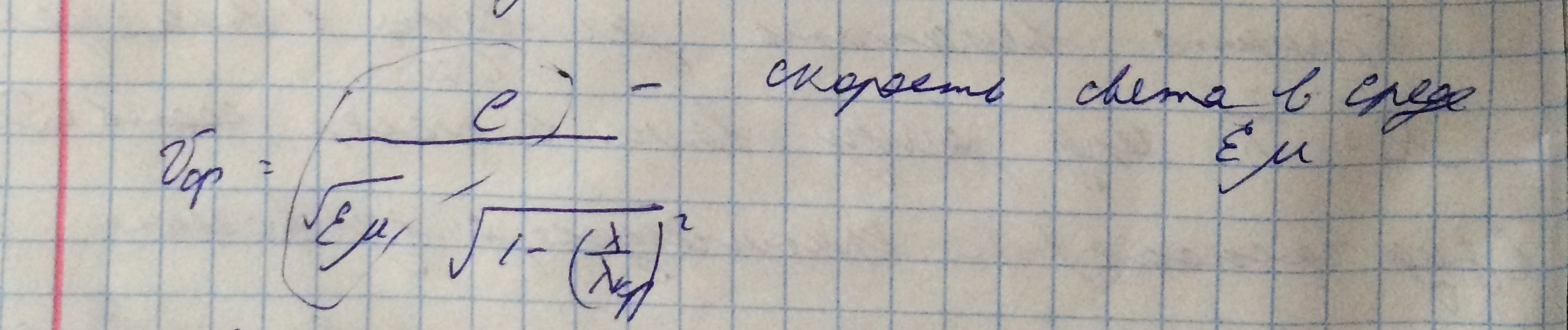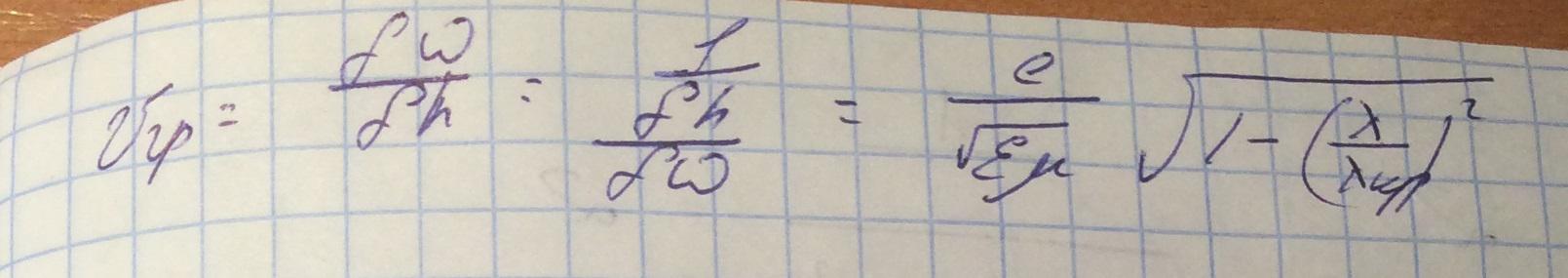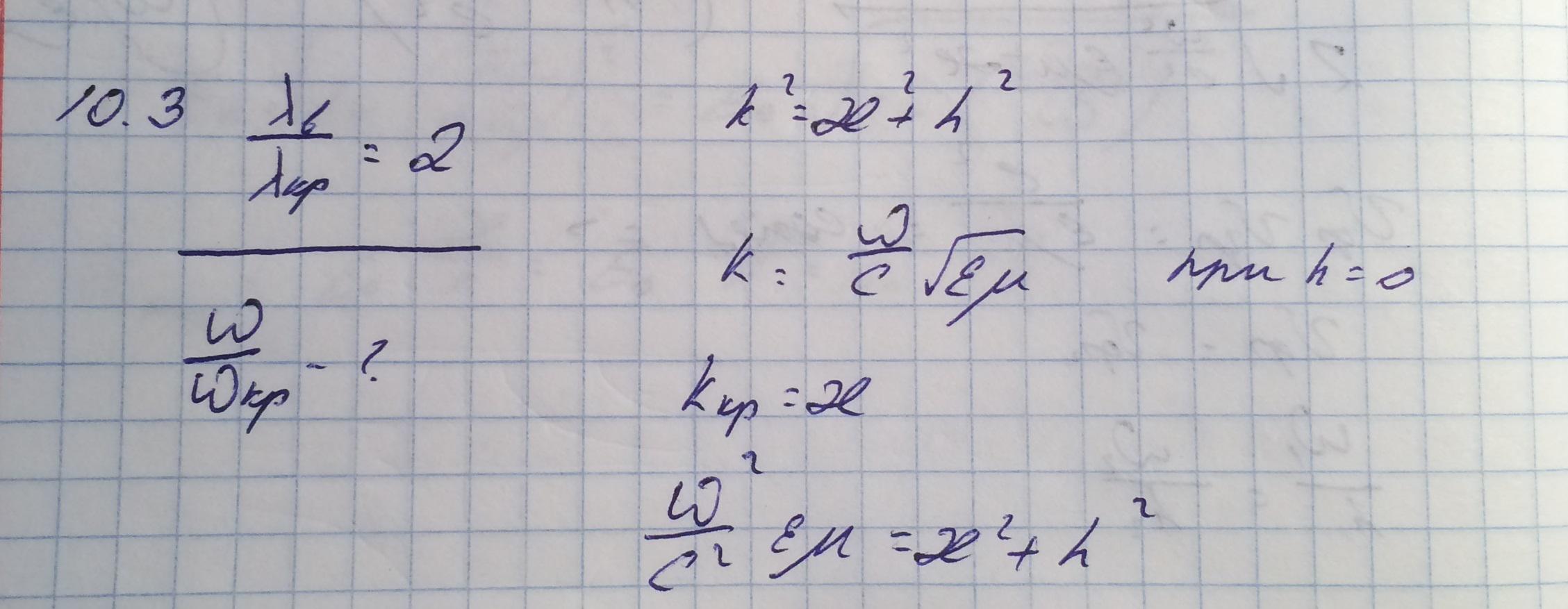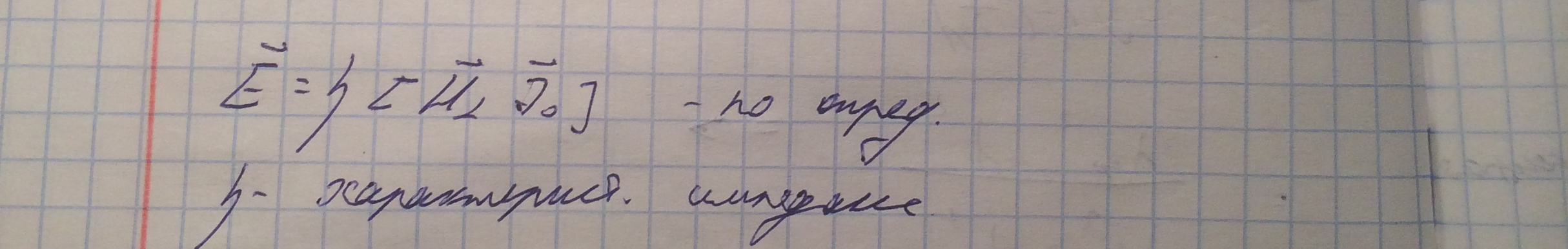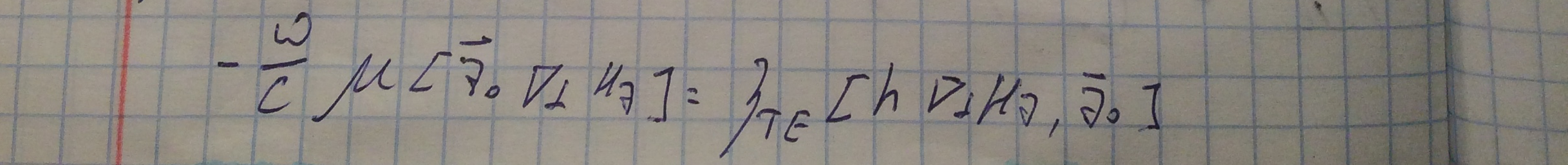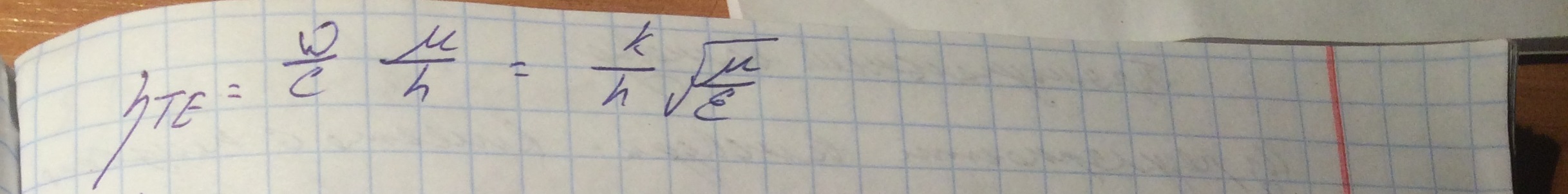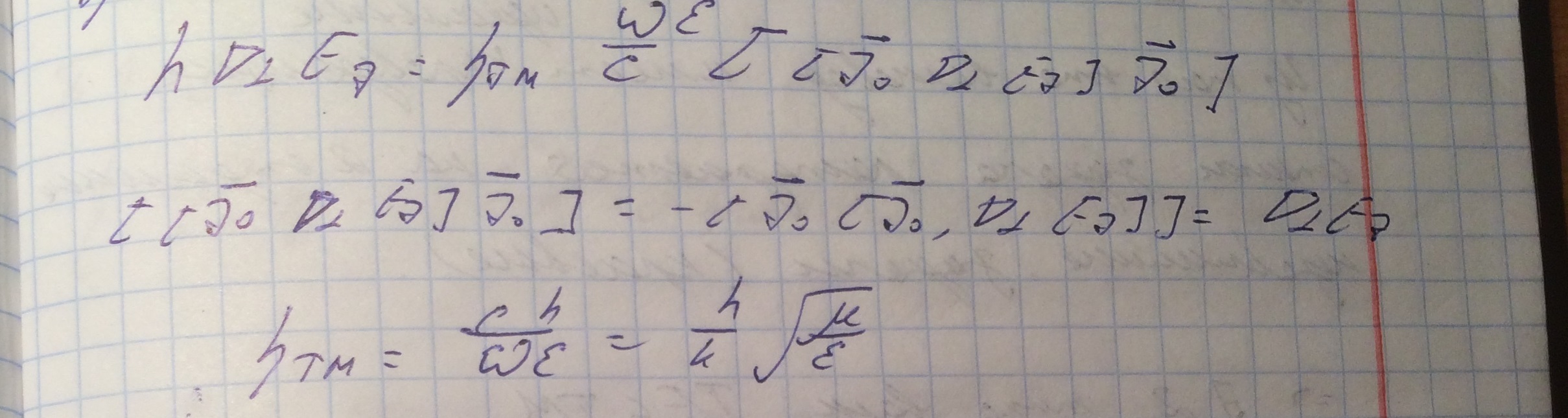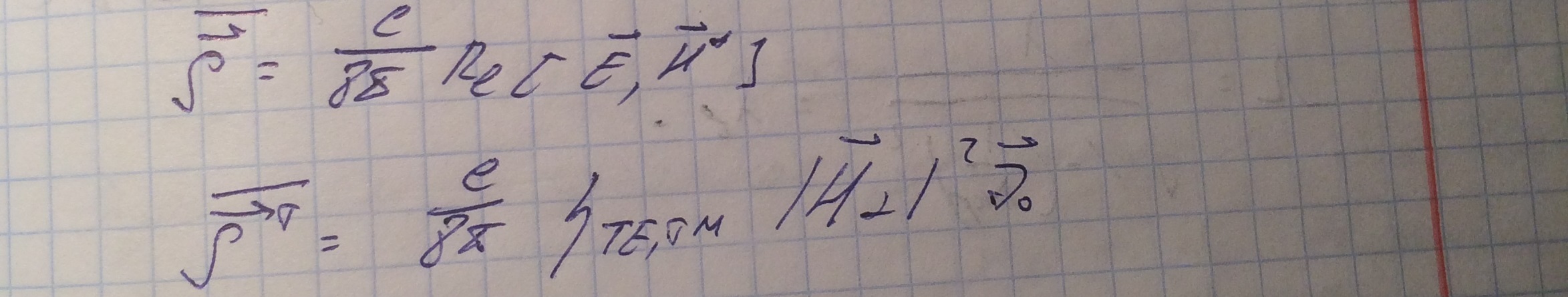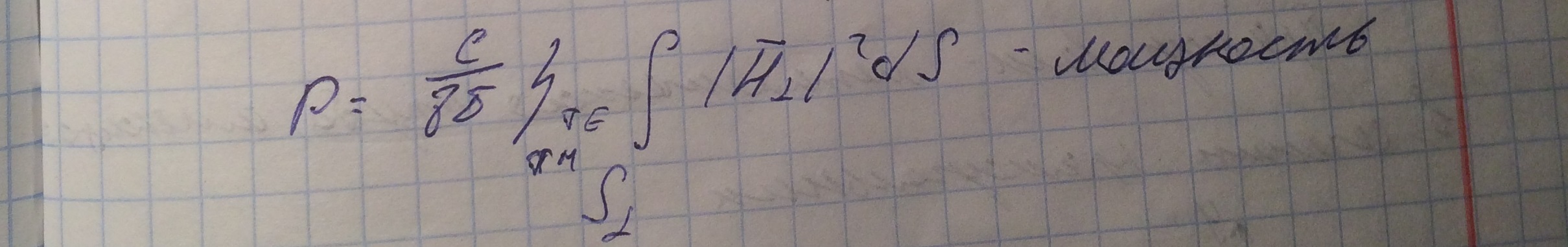Уравнения полей в волноводе
Рассмотрим регулярный волновод, при условии, что в нем нет источников.
Запишем уравнения Максвелла для комплексных амплитуд.
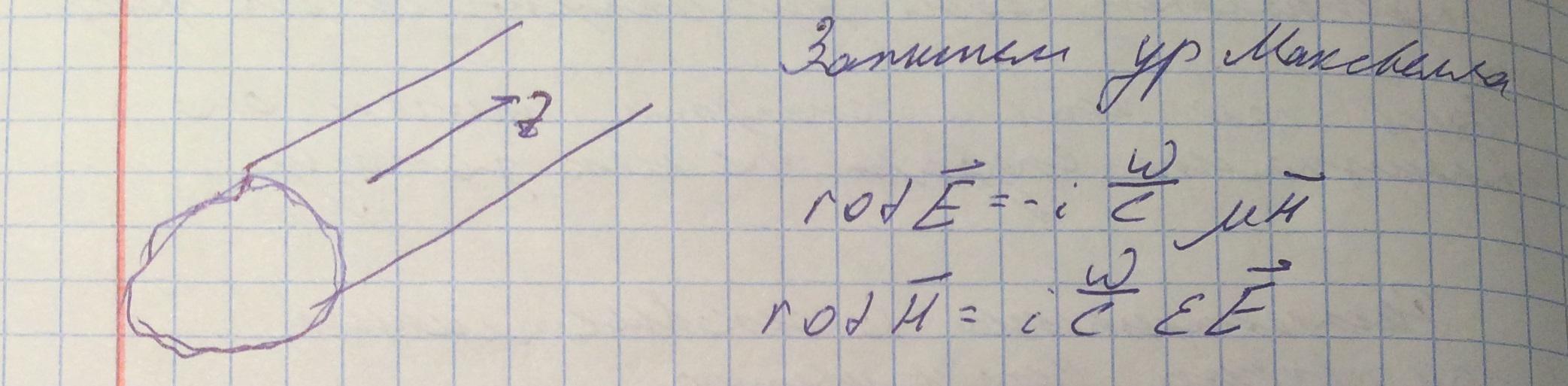
Будем ожидать, что в этой структуре распространяется однородная, плоская бегущая волна.
Выражение для вектора напряженности электическго поля запишем в следующем виде:
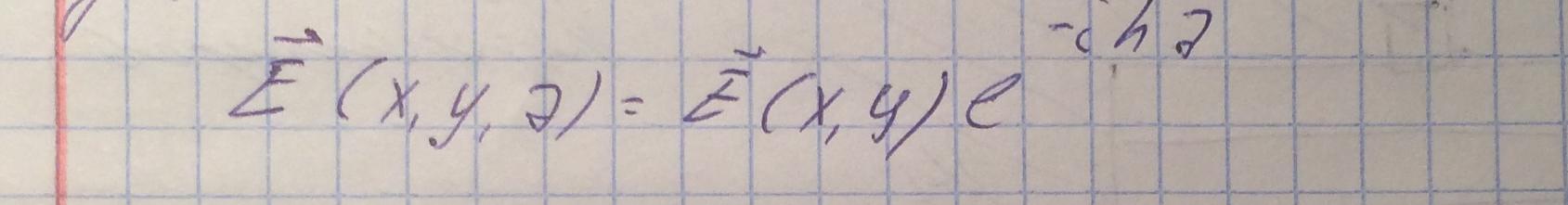
А для вектора напряженности магнитного поля:
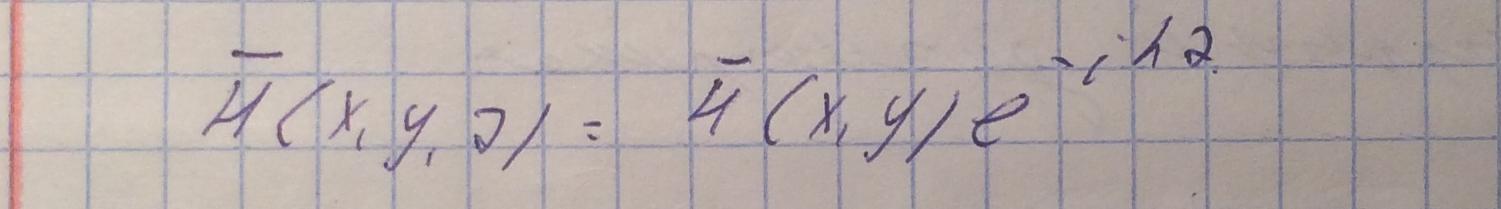
Где h=const - продольное волновое число, которое определяется типом волны.
Подставим ожидаемые решения в уравнения Максвелла.
Переходя к записи ротора в декартовой системе координат для двух предыдущих уравнений и, группируя соответствующие компоненты, получим следующие выражения :
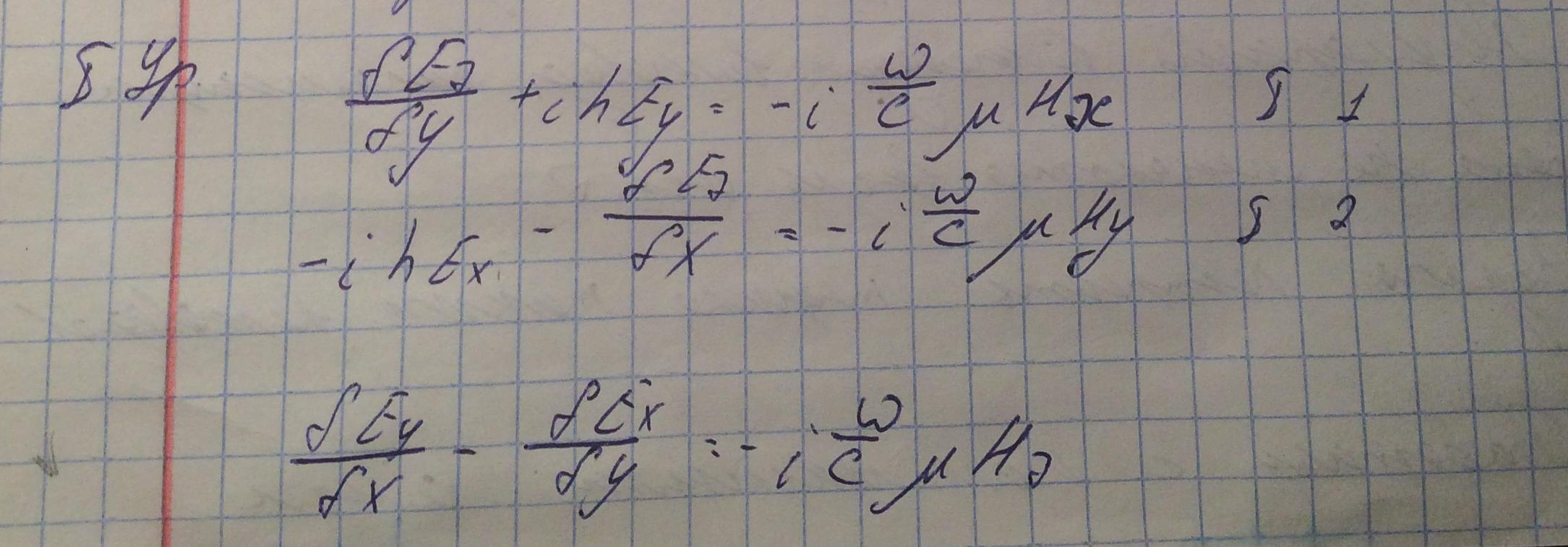

Из данных двух систем получим выражения, представляющие значения поперечных компонент электромагнитного поля через производные от продольных компонент:

В исходной задаче было 6 неизвестных волновых компонент, но с помощью приведенных выше упрощений пришли к двум продольным неизвестным Ez и Нz.
Запишем предыдущие выражения в компактной форме:
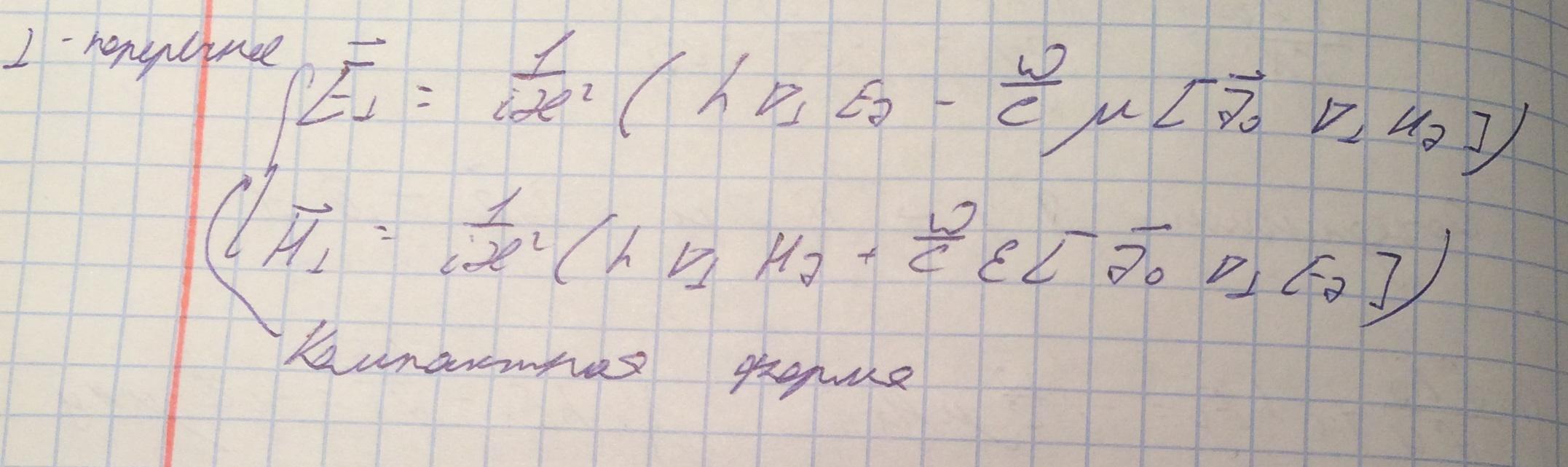
Для нахождения продольных компонент Ez и Hz воспрользуемся волновым уравнением:
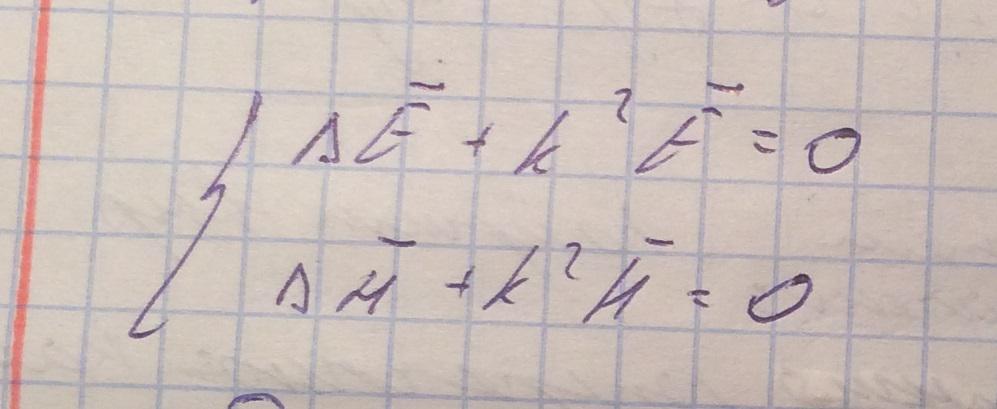
В данном случае нас интересуют только Ez и Hz компоненты, которые представимы в виде:
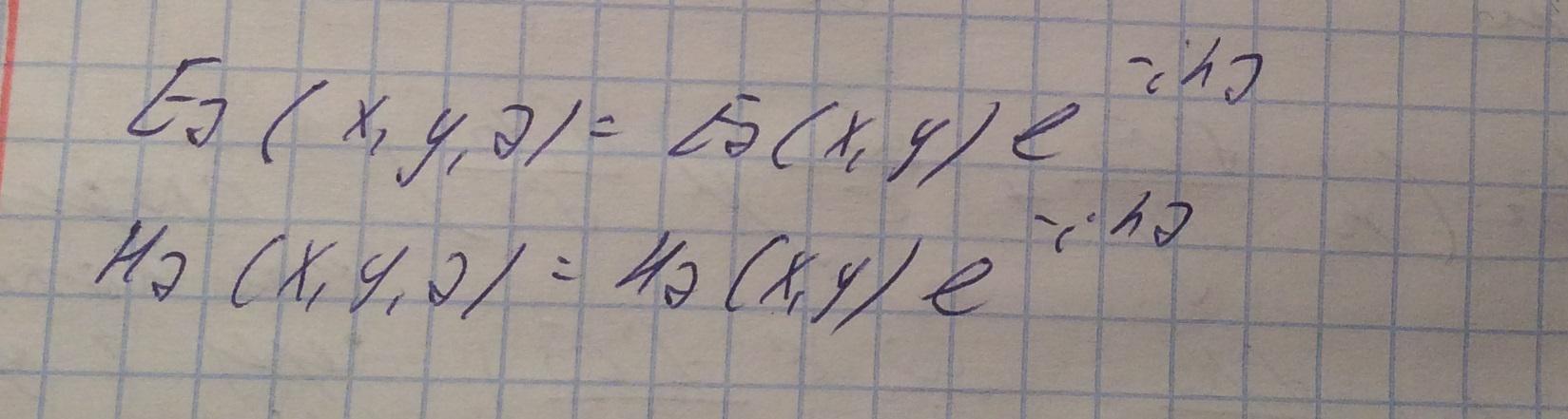
Подставим ожидаемые решения в волновые уравнения в результате чего получим уравнение Гемгольца:
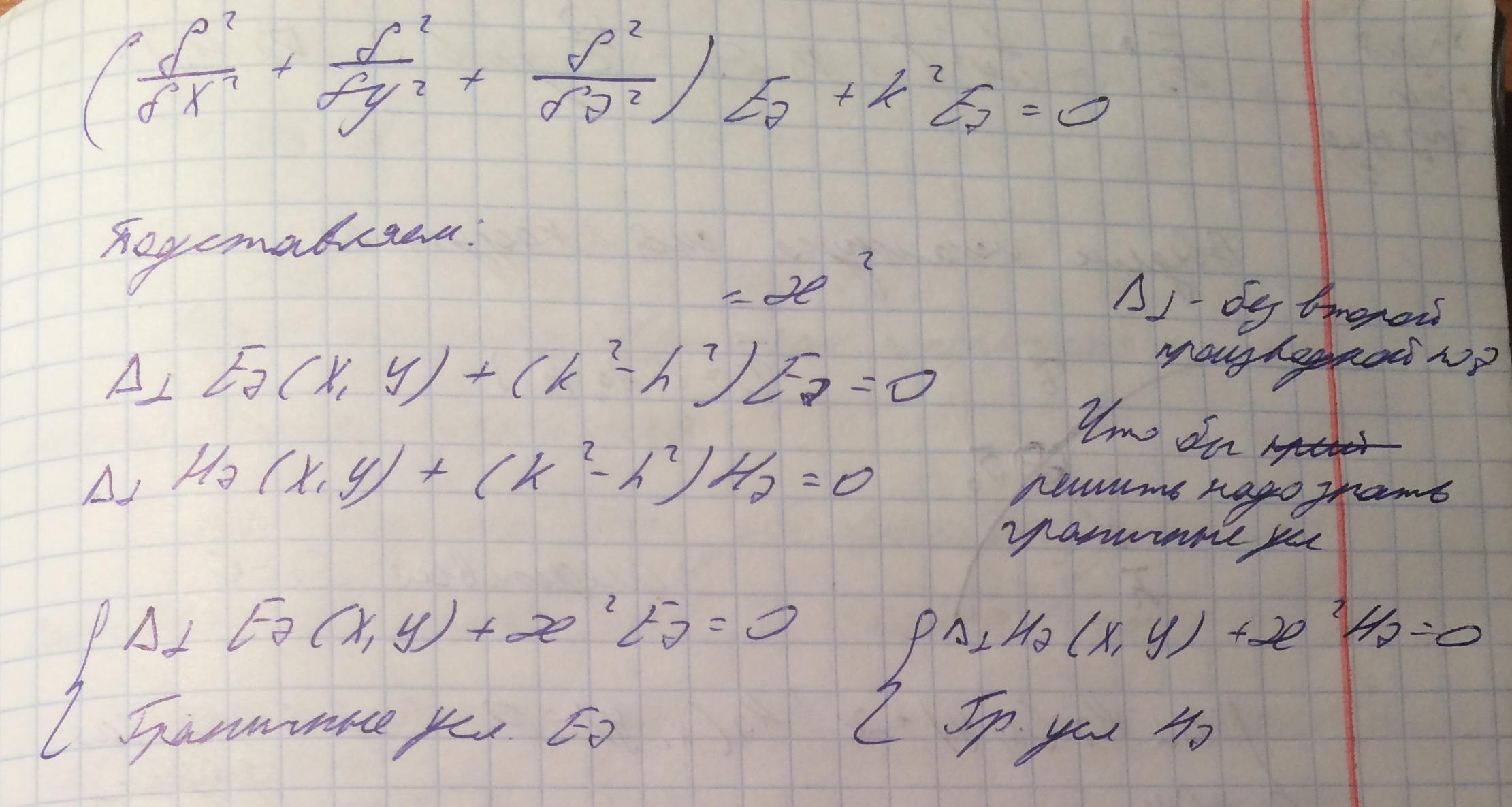
Теперь определим граничные условия.
Будем рассматривать полые волноводы с идеально проводящими стенками, при этом форму сечения не конкретизируем.
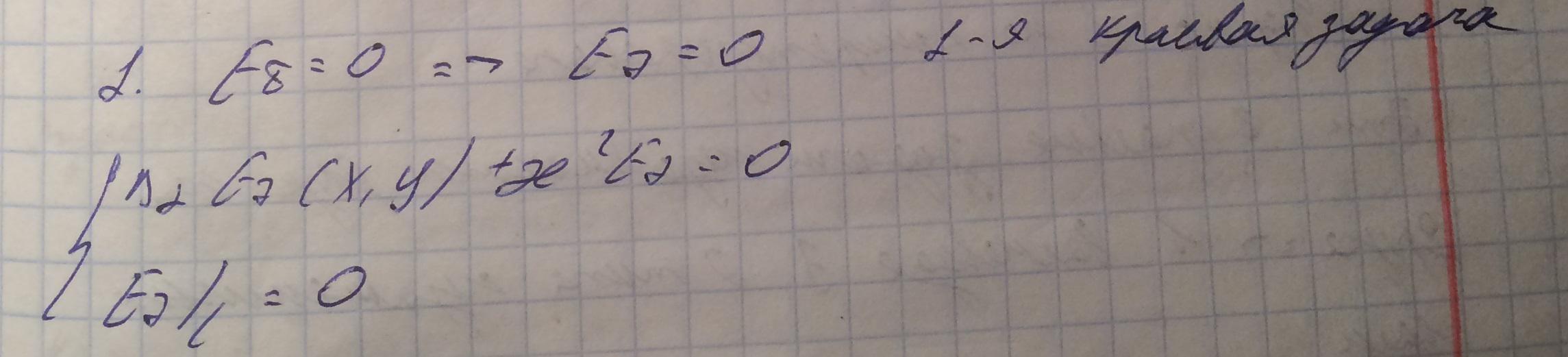
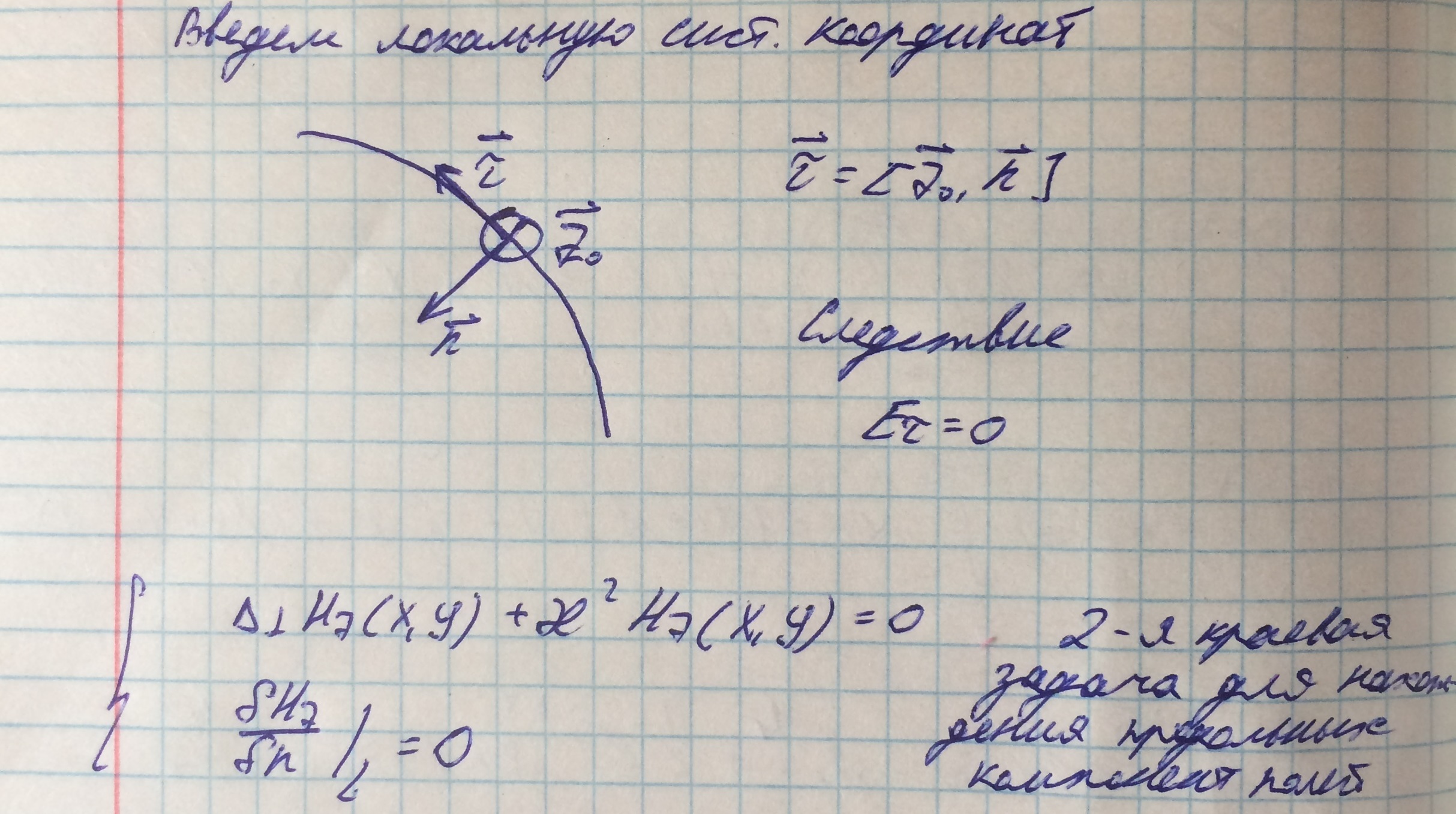
Граничное условие во второй краевой задачи получается в силу равенства тангенсальной компоненты электрического поля и представлении его в веденной системе координат.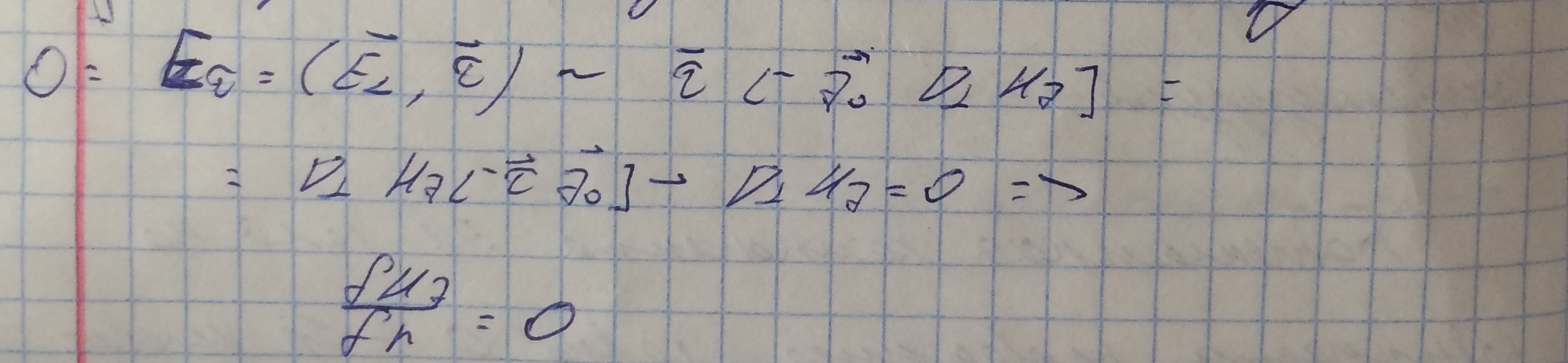
В результате получили две краевые задачи, которые независимы друг от друга, следовательно в волноводе существует два типа независимых волн.
1. E волна или TM волна, магнитное поле в которой поперечное;
2. H волна или TE волна, электрическое поле в которой поперечное.
При этом существует тип волны, в которой присутствуют как поперечные, так и продольные составляющие полей - TEM волна.
В математической физике это две краевые задачи на собственные функции и собственные числа.
Решение данных задач возможно при конкретных собственных числах, являющихся попречными волновыми числами, а решения соответствующие данным собственным числам носят название собственных функций.
Конкретный вид границы будет определять собственные числа краевой задачи.
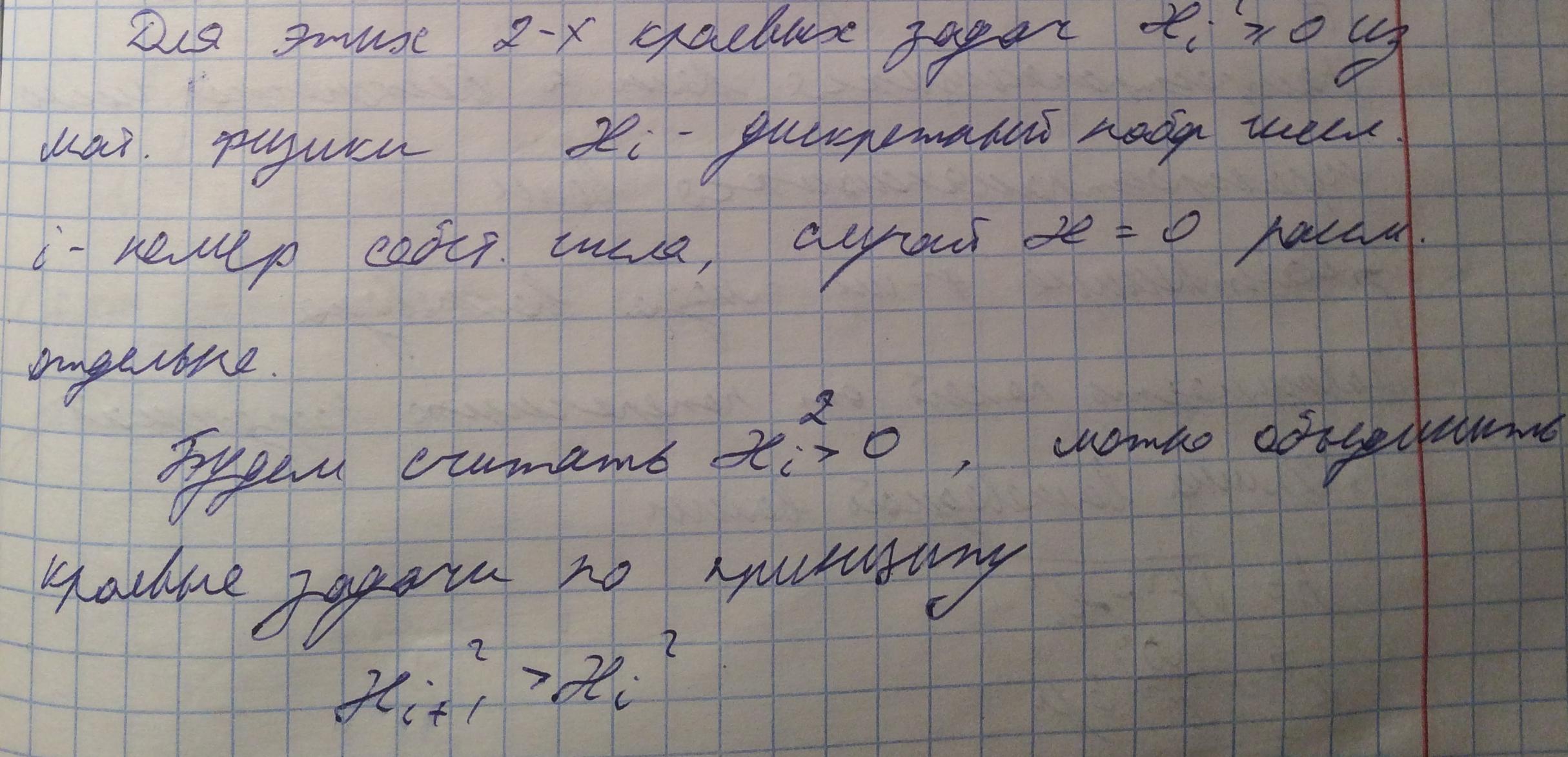
То есть в нашем случае набор собственных чисел возрастающий.
Рассмотрим такой бесконечный набор:
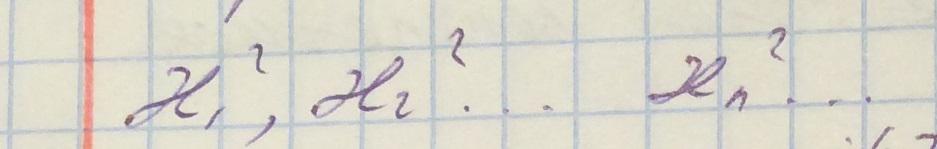
При этом поперечные и продольные составляющие волнового числа связаны дисперсионным уравнением, которое получается из волнового уравнения:
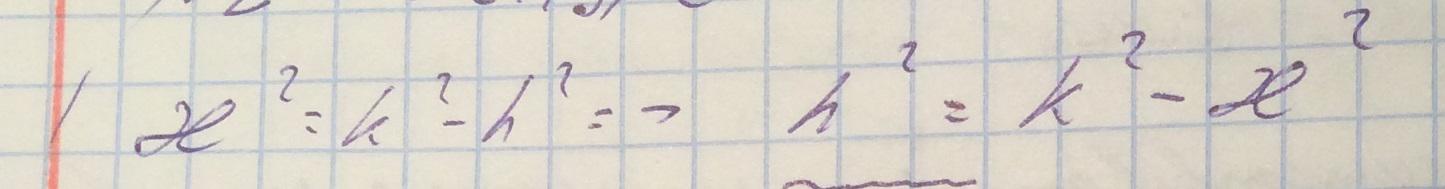
Подставляя продольное волновое число в уравнения полей
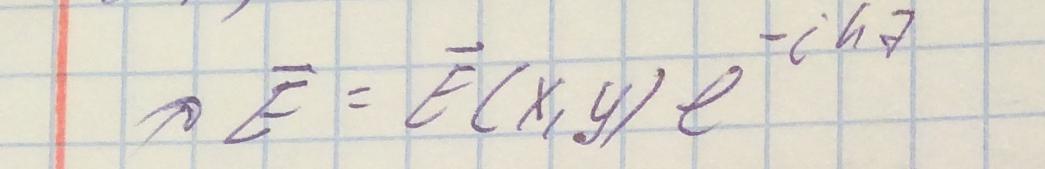
Из данных зависимостей следует, что если продольное волновое число действительное, то волна распространяющаяся, а если мнимое, то волна экспоненциально убывающая. Значит существует граница между типами волн. Можно заметить, что при любой заданной частоте в волноводе с идеально проводящими стенками всегда существует конечное число распространяющихся волн и бесконечное число нераспространяющихся волн.
Обозначим:

Введем вспомогательные понятия:
1. Критическая частота (критическая частота в волноводе) - частота, при которой волны в волноводе перестают быть распространяющимися
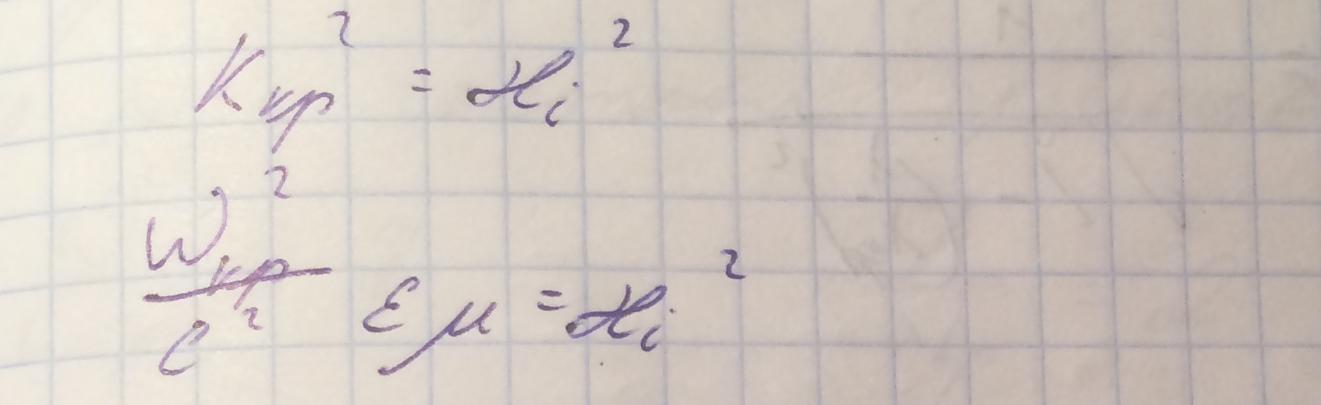
Длина волны в свободном пространстве, соответствующая критической частоте носит название критической длины волны
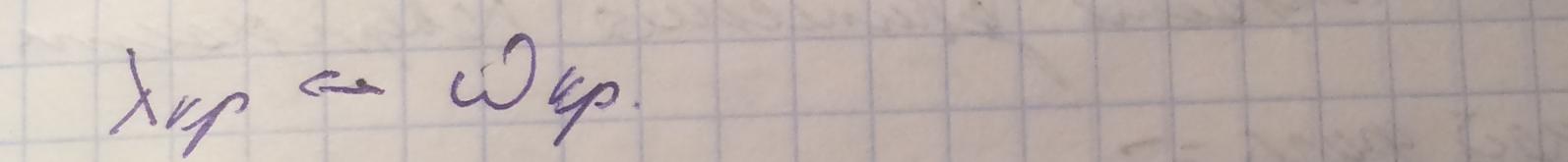
Принято выражать длину волны в волноводе через длину волны в свободном пространстве и критическую длину волны данной моды.

2. Фазовая скорость волны в волноводе - скорость распространения фазового фронта волны.
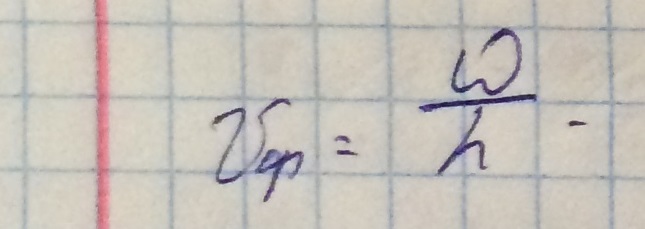
При этом справедливо выражение: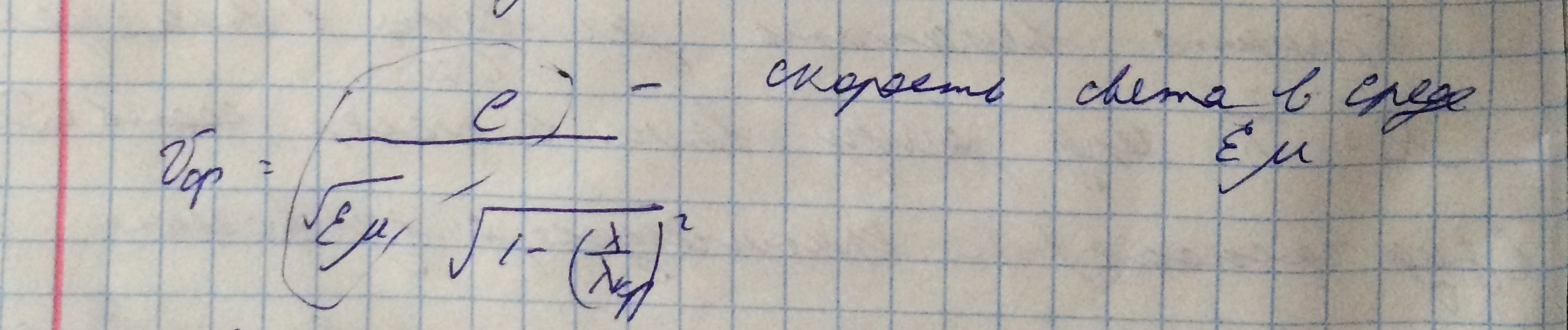
В идеально проводящем волноводе фазовая скорость всегда больше фазовой скорости в свободном пространстве.
3. Групповая скорость - определяет скорость переноса энергии и информации.
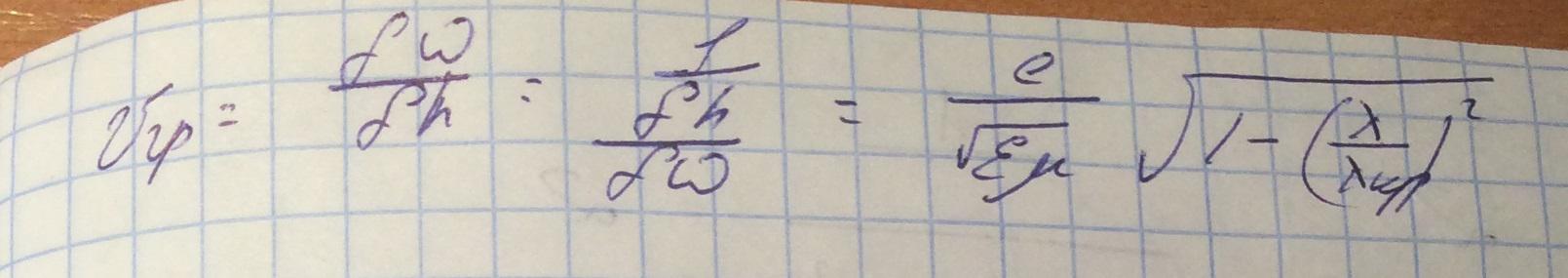
В идеально проводящем волноводе групповая скорость всегда меньше фазовой скорости в свободном пространстве.
Характеристический импеданс мод волновода и энергетические соотношения
Что бы определеть характеристический импеданс TE и ТМ волн необходимо воспользоваться граничным условием Леонтовича.
Характеристический импеданс имеет разные значения для ТЕ и ТМ волн. Определим их.
1. Для ТЕ волны. Следующие соотношения получаются из уравнений, связывающих попереченые компоненты полей с продольными и последующей подстановкой подстановкой в них граничного условия Леонтовича.
2. Аналогично для ТМ волны:
Определим выражения для
вектора Пойтинга, который характеризует средний по времени поток энергии через единицу поверхности.
При этом переносимая волноводом мощность равна:
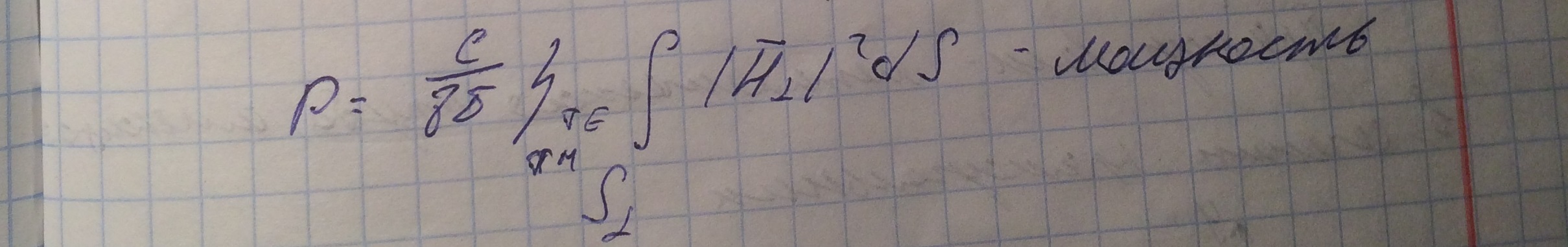
Дополнительную информацию о полях в волноводе можно узнать по
ссылке.Ссылка на оглавление.