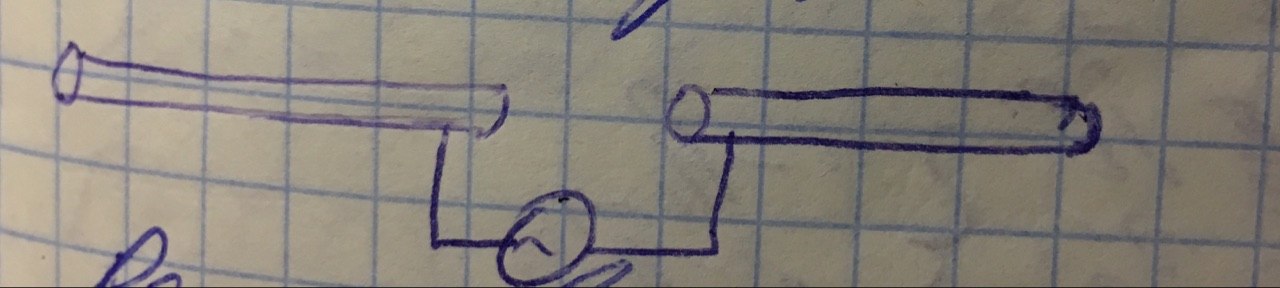
Рассмотрим возбуждение волноводов с заданными гармоническими источниками.
Есть волновод, в котором имеется область с заданными токами. Нужно определить, как эти токи будут создавать поле во всём волноводе.
Рассмотрим неоднородное пространство, у которого ε(r), μ(r), σ(r);
Пусть в этом пространстве задано 2 распределения токов и связанных с ним 2 распределения полей:
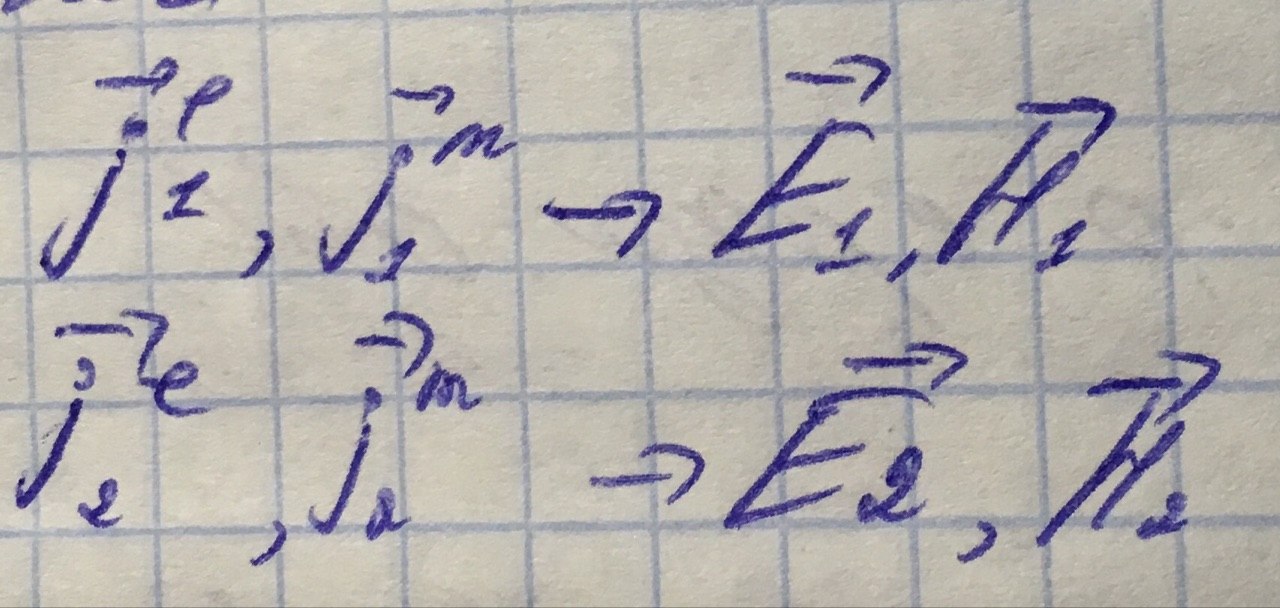
Запишем 2 группы уравнений Максвелла:


Проинтегрируем (*) по произвольному объему V, ограниченному поверхностью S:
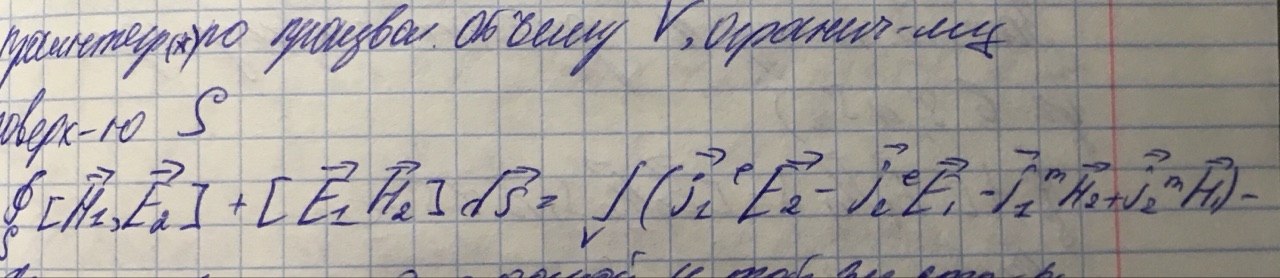
Нужно найти для каждой моды связь:

Рассмотрим пустой волновод (т.е. волновод, в котором нет источников):

Запишем Лемму Лоренца для этих 2-х мод (для участков S1 и S2):

Поверхности S1 и S2 произволные. Это означает, что интеграл Ipq не зависит от z:
Возьмем другой волновод (с полями):

Запишем для этих полей лемму Лоренца:

Заменим порядок суммирования и интегрирования.
Отличным от нуля является только интеграл по S2.
