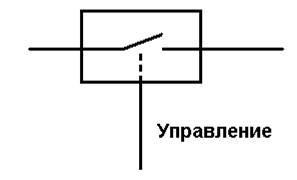
В основе цифровой электроники лежит использование ключевых режимов работы полупроводниковых приборов. В таком режиме полупроводниковый транзистор может рассматриваться как устройство, сопротивление между двумя электродами которого управляется третьим электродом, причем в одном из состояний сопротивление близко к нулю (ключ замкнут), а в другом – бесконечно велико (ключ разомкнут). Механическая модель транзистора показана на рис.1.1. 

Рис.1.1. Механическая модель транзистора.

Из подобных элементов может быть построена схема, состояние которой может быть описано двумя уровнями напряжения – низким и высоким. С целью увеличения помехоустойчивости для каждого уровня выбирается некоторый диапазон значений напряжения, обеспечивающий устойчивое считывание состояния цифрового выхода входами других цифровых узлов (рис.1.2)

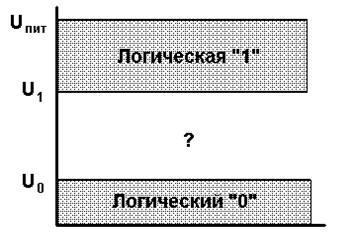
Рис.1.2. Логические уровни в цифровых устройствах.

Напряжения, меньшие некоторого минимального значения U0, трактуются как логическая величина «ноль», а большие некоторого U1 – как «логическая единица». Напряжение питания естественным образом ограничивает диапазон возможных значений напряжения – нижним пределом логического нуля является нулевое напряжение, а верхним пределом логической единицы – напряжение питания. Таким образом, с помощью значений напряжения можно представить простейшие сигналы, принимающие только два значения. Однако кроме передачи логического уровня, требуется и преобразование сигналов, что также обеспечивается полупроводниковыми устройствами.

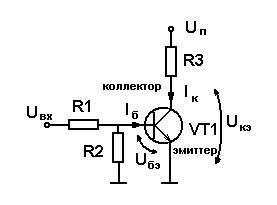
Рис. 1.3. Простейший инвертор на биполярном транзисторе.

На рис.1.3. изображена упрощенная схема инвертора на биполярном транзисторе. Принцип работы данной схемы можно понять, если учесть, что при наличии тока базы транзистор уменьшает сопротивление между выводами эмиттера и коллектора («открывается»), а при отсутствии – увеличивает («закрывается»). Резисторы R1 и R2 служат для ограничения тока базы, а R3 ограничивает максимальный ток коллектора. Теперь, если на вход данной схемы будет подано напряжение, соответствующее логической единице, управляющий ток базы откроет транзистор, и сопротивление между эмиттером и коллектором резко уменьшится. Следовательно, напряжение на коллекторе будет близко к нулю. Если же напряжение на входе будет близко к нулю, ток базы будет слишком мал для открывания транзистора, и напряжение на коллекторе будет определяться током, протекающим от источника питания через резистор R3. Таким образом, логический уровень на выходе данной схемы всегда противоположен логическому уровню на ее входе. Такое устройство и называется инвертором.

Показанная на рис.1.3. схема является сильно упрощенной и не соответствует схемотехнике промышленных цифровых микросхем. Тем не менее, она позволяет ознакомиться с принципом использования биполярных транзисторов для создания цифровых схем. В реальных устройствах используется первичное преобразование электрических сигналов, которое обычно также выполняется с помощью транзисторов. Вследствие этого одна из наиболее распространенных архитектур цифровых систем носит название «транзисторно-транзисторная логика», или ТТЛ. Такое название отражает тот факт, что транзисторы используются как для первичного преобразования сигналов, так и для формирования выходного напряжения. Предшественниками такой архитектуры являются резисторно-транзисторная (показанная на рис.1.3) и диодно-транзисторная логика.

Существенным недостатком микросхем ТТЛ является наличие статического потребления – для удержания биполярного транзистора в открытом состоянии требуется протекание постоянного тока базы, поэтому использование биполярных транзисторов в цифровых устройствах ограничено максимальной рассеиваемой мощностью.

Альтернативным вариантом является построение цифровых устройств на полевых транзисторах, которые управляются потенциалом затвора и не требуют постоянного протекания управляющего тока. Удобнее использовать полевые транзисторы, выполненные по технологии «металл-окисел-полупроводник», МОП. В зависимости от типа проводимости канала такие транзисторы могут открываться либо низким логическим уровнем (транзисторы с p-каналом), либо высоким (транзисторы с n-каналом). Использование транзисторов, аналогичных по характеристикам, но имеющих разный тип проводимости канала (комплементарных, т.е. «дополняющих») позволяет реализовать эффективный инвертор (рис.1.4.).

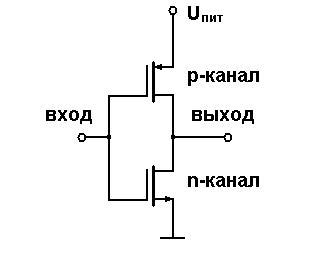
Рис.1.4. Принципиальная электрическая схема инвертора КМОП.

На схеме рис.1.4. верхний транзистор открывается при низком логическом уровне, подключая к выходу напряжение питания (т.е. обеспечивая высокий уровень выходного напряжения). При высоком входном уровне верхний транзистор закрывается, а нижний – открывается и подключает к выходу уровень нуля. Статическое потребление такой схемы определяется утечками тока через слой диэлектрика между затвором и каналом, т.е. весьма мало. Большую роль играет так называемое динамическое потребление: в процессе переключения входного напряжения существует период времени, в течение которого оба транзистора обладают конечным сопротивлением, и наблюдается протекание тока через оба канала (в статическом состоянии один из транзисторов почти полностью открыт, а другой – почти полностью закрыт). При этом мощность, потребляемая схемами КМОП, оказывается приблизительно пропорциональной частоте переключения внутренних сигналов.

Приведенные выше сведения о схемотехнике цифровых устройств являются сильно упрощенными и не отражают целый ряд вопросов. Например, уменьшение норм технологического процесса и размеров транзисторов приводит к тому, что сопротивление диэлектрика между затвором и каналом также уменьшается, что приводит к резкому росту утечек тока. Не рассмотрено также поведение транзисторных ключей в динамическом режиме, подключение нагрузки к выходам, особенности технологических процессов изготовления цифровых устройств и многое другое. Для подробного изучения схемотехники цифровых элементов следует обратиться к специальной литературе.

Инвертор не является единственным устройством для преобразования логических сигналов. Более того, интерес представляют как раз не одновходовые, а многовходовые  устройства, позволяющие сформировать сигнал, представляющий собой сложную функцию от состояния входов. Набор базовых логических элементов представлен на рис. 1.5.

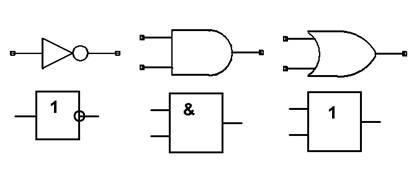
Рис. 1.5. Базовые логические элементы: логическое НЕ (инвертор), логическое И, логическое ИЛИ. Верхний ряд – изображение по IEEE, нижний ряд – по ЕСКД.

Логические элементы называются также вентилями (в англоязычной литературе gate). Необходимо обратить внимание, что таким же термином обозначается затвор полевого транзистора, хотя смысловая нагрузка в этих случаях различна.

Удобным способом описания работы логических вентилей является составление таблиц истинности. В такую таблицу записывается состояние выхода в зависимости от комбинации входных сигналов. Для элементов, показанных на рис. 1.5., таблицы истинности будут выглядеть следующим образом.

Таблица 1.1.

Таблицы истинности для базовых логических элементов

Число входов для логических элементов Ии ИЛИ может быть больше двух. При этом сохраняется принцип работы, показанный в таблице 1.1: на выходе элемента И логическая 1 появляется только в том случае, если все входы находятся в состоянии логической 1 («И на первом, И на втором, И на третьем…»), а для появления логической 1 на выходе элемента ИЛИ достаточно наличия логической 1 хотя бы на одном из его входов. Имея двухвходовые логические элементы, можно создать такой же элемент с числом входов больше двух, соединяя одинаковые элементы последовательно, как это показано на рис.1.6.

С помощью базовых логических элементов можно формировать и более сложные схемы, которые будут описываться сложными таблицами истинности. Для упрощения построения таких схем вводятся вспомогательные логические элементы. Основными их разновидностями являются: вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ, схемы И-НЕ, ИЛИ-НЕ. Графические обозначения этих вентилей показаны на рис. 1.7., а таблицы истинности приведены в табл.1.2.

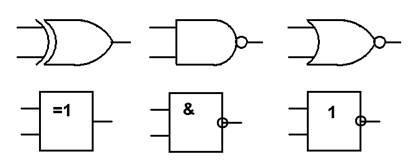
Рис. 1.7. Вспомогательные логические элементы: ИСКЛЮЧАЩЕЕ ИЛИ, И-НЕ, ИЛИ-НЕ. Верхний ряд – изображение по IEEE, нижний ряд – по ЕСКД.

Таблица 1.2.

Таблицы истинности для вспомогательных логических элементов

Из табл. 1.2. видно, что элемент ИСКЛЮЧАЩЕЕ ИЛИ формирует на выходе логическую 1, когда логические уровни на его входах различны. Его можно также рассматривать как элемент ИЛИ, за исключением состояния «оба входа равны 1».

Элементы И-НЕ и ИЛИ-НЕ могут быть получены путем последовательного соединения элементов И, НЕ и ИЛИ, НЕ соответственно. Для упрощения графического изображения символ инверсии (небольшой кружок) размещают непосредственно на выходе такого элемента. Часто в обозначении элемента указывается и число его входов. Например, 3ИЛИ соответствует трехвходовому элементу ИЛИ.

Символы инверсии могут быть размещены и на входах логических элементов. В этом случае их работу необходимо анализировать так, как если бы сигнал на этот вход подавался через элемент НЕ.

Рассмотрим двухвходовой элемент И-НЕ (2И-НЕ). Если объединить его входы, то таблицу истинности можно представить следующим образом.

Таблица 1.3.

Таблицы истинности для элемента 2И-НЕ с объединенными входами

Из этой таблицы следует, что элемент 2И-НЕ в данном случае выполняет функцию инвертора.

Соединив элементы 2И-НЕ и инвертор, созданный из такого же элемента с объединенными входами, получаем элемент 2И. Обращаясь к рис.1.6., убеждаемся, что теперь можно получить элемент И с произвольным числом входов.

Наконец, вводя инверторы для входных сигналов, получаем следующую таблицу истинности (в скобках показаны значения инвертированных сигналов, которые в действительно воспринимаются элементом 2И-НЕ).

Таблица 1.4.

Таблицы истинности для элемента 2И-НЕ с инвертированными входами

Итак, для элемента 2И логическая единица на выходе должна появиться только в том случае, если оба сигнала, стоящие в скобках, равны 1. В остальных случаях на выходе присутствует логический ноль. С учетом инвертора, стоящего на выходе, получаем результаты, показанные в табл.1.4. Нетрудно убедиться, что они соответствуют логике работы элемента 2ИЛИ.

Таким образом, имея достаточное количество элементов 2И-НЕ, можно реализовать любой из элементов И, ИЛИ, НЕ. Поэтому элемент 2И-НЕ может выступать в роли некоторого эквивалента сложности комбинаторной схемы. Аналогичные рассуждения можно провести и для элемента 2ИЛИ-НЕ, с помощью которого также реализуются любые схемы комбинаторной логики. Элементы 2И-НЕ (называемый также базисом Шеффера) и 2ИЛИ-НЕ (базис Пирса) являются так называемыми эквивалентными логическими вентилями (equivalentlogicgates), с помощью которых можно оценить сложность того или иного цифрового устройства.

Особенностью работы представленных логических элементов является то, что соответствующий таблице истинности сигнал на их выходе появляется с незначительной задержкой относительно смены состояний на входе. Эта задержка обусловлена только процессами переключения элементов схемы и при рассмотрении идеальных элементов считается, что она равна нулю. Таким образом, изменение уровня выходного сигнала может произойти в любой момент времени, поэтому такие схемы относят к классу асинхронных. Однако более точным названием, отражающим использование логических вентилей, состояние которых определяется только уровнем входного сигнала, является термин «комбинаторная логика» (combinatory). Действительно, для точного определения состояния выхода такой схемы достаточно знать комбинацию состояний ее входов. При этом предыстория их изменений не играет роли. Существуют также устройства, состояние которых может также измениться в любой момент времени, но определяется не только текущим состоянием входов, но и историей изменения этих состояний.

На базе устройств комбинаторной логики возможно решение многих задач вычислительной техники. В частности, с их помощью производится выполнение базовых арифметических операций.

Рассмотрим операцию сложения, выполняемую над числами, представленными в двоичной системе счисления. В этой системе возможны всего четыре варианта: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1+1=10 (210). Для представления числа 2, которое в двоичном виде запишется как 10, требуется уже два разряда.

Запишем таблицу истинности для элемента, устанавливающего выход в соответствии с младшим разрядом результата сложения двух чисел, представленных в двоичной системе.

Таблица 1.5.

Таблица истинности одноразрядного сумматора.

В последнем случае в таблице записан ноль, поскольку произошел перенос в следующий разряд. Из таблицы видно, что операция сложения реализуется элементом ИСКЛЮЧАЮЩЕЕ ИЛИ.

Для представления числа, переносимого в следующий разряд, потребуется еще один выход. Нетрудно убедиться, что значение этого выхода равно 1 только в том случае, когда оба входа равны 1 – сигнал переноса, таким образом, формируется элементом И.

При сложении многоразрядных двоичных чисел необходимо учитывать сигналы переноса, приходящие из предыдущих разрядов, и формировать такие сигналы для последующих разрядов. С учетом сигнала переноса, каждый элемент сумматора, начиная со второго, должен иметь три входа вместо двух. Обозначим вход переноса как Cin, а выход как Cout и составим таблицу истинности для такого блока.

Таблица 1.6.

Таблица истинности одного разряда многоразрядного сумматора.

При составлении таблицы истинности использовалось свойство коммутативности сложения: поскольку порядок слагаемых не влияет на результат, можно ориентироваться на то, что нечетное число единиц в трех входных сигналах обуславливает появление единицы на выходе Q, а выход Cout принимает значение 1 в тех случаях, когда два или три входа находятся в состоянии единицы. Можно подобрать несколько вариантов реализации устройства комбинаторной логики, реализующего сложение.

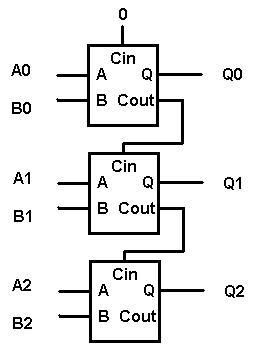
Рис. 1.8. Многоразрядный сумматор.

Элементы комбинаторной логики реализуются цифровыми микросхемами малой степени интеграции. Это серии 155, 555, 1533 и др. российского производства и их аналоги 74xx, выполненные по технологии ТТЛ, а также КМОП-устройства серий 176, 561 и 54xx соответственно. В составе этих серий присутствует большое количество элементов рассмотренных выше типов с различным числом входов.

Немаловажным является тот факт, что заданная таблица истинности может быть в общем случае получена более чем одним способом соединения стандартных микросхем комбинаторной логики. Эти способы могут отличаться различным числом используемых вентилей, корпусов микросхем, суммарными задержками распространения сигналов и т.п. Поэтому при использовании дискретных микросхем комбинаторной логики весьма важной является задача получения схемотехнического решения, минимизирующего число использованных корпусов и/или наименований микросхем, для чего используются приемы эквивалентного преобразования логических выражений, подробно описанные в специальной литературе. С развитием технологии изготовления интегральных микросхем, а особенно с учетом возможностей микросхем программируемой логики, рассматриваемых в данном курсе, вопросы минимизации схем комбинаторной логики существенно теряют актуальность, поскольку, как будет подробно рассмотрено в последующих главах, в программируемых микросхемах с архитектурой FPGA занимаемый объем и вносимые задержки зависят только от числа входов комбинаторной схемы, но не от вида реализуемой функции.

В противоположность асинхронным, синхронные цифровые устройства изменяют состояние выходных сигналов в строго определенные моменты времени. Эти моменты, как правило, соответствуют положительному перепаду специального синхронизирующего сигнала, называемого проще тактовым сигналом. Для описания работы синхронных устройств может использоваться такое представление, как временные диаграммы работы. Они представляют собой графики зависимости логических уровней от времени, на которых показывают типичные комбинации и события (перепады уровня) на входных линиях, а также соответствующие изменения выходных сигналов. Базовым синхронным элементом является D-триггер. Его графическое изображение и временные диаграммы работы показаны на рис. 1.9.

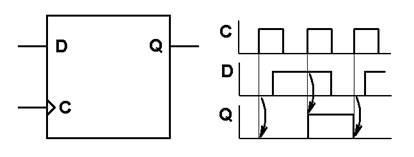
Рис. 1.9 Графическое изображение и временные диаграммы работы D-триггера.

На рис.1.9. видно, что выход триггера Q принимает то же состояние, что было на входе данных D, в момент положительного перепада (фронта) тактового сигнала. В остальные моменты времени изменения логического уровня на входе D никак не влияют на состояние выхода. Такое поведение позволяет, в частности, использовать D-триггер в качестве устройства хранения данных. После подачи на вход D требуемого уровня сигнала и запоминания его в триггере по фронту тактового сигнала значение с входа данных D может быть убрано. При этом возникает проблема: как добиться того, чтобы последующие фронты тактового сигнала не переписывали запомненное в триггере значение? Одним из способов является формирование вспомогательного тактового сигнала с помощью элемента 2И. На первый из входов этого вентиля подается собственно тактовый сигнал, а на второй – сигнал разрешения. Обращаясь к таблице истинности 2И, нетрудно убедиться, что если на втором входе будет присутствовать сигнал логического нуля, то выход этого элемента будет оставаться в нуле при любом уровне тактового сигнала. Если же на вход разрешения подан сигнал логической единицы, то состояние выхода полностью определяется состоянием входа, на который подан тактовый сигнал. Таким образом, элемент 2И может запрещать прохождение тактового сигнала на вход C триггера в те периоды времени, когда обновление его состояния не требуется.

В ряде случаев введение в проект вспомогательных вентилей, запрещающих прохождение тактового сигнала, ведет к труднообнаружимым ошибкам. Их источником является тот факт, что тактовый сигнал, прошедший через логический вентиль, оказывается задержанным относительно исходного сигнала на время, требуемое для переключения внутренних схем элемента 2И. Это приводит к тому, что фронт тактового сигнала приходит на разные триггеры в разные моменты времени, и часть триггеров проекта, срабатывая раньше, может исказить логические сигналы, требующие записи в остальные триггеры. Этот неприятный эффект носит название «гонки фронтов», и его следует всячески избегать. Для исключения записи в неподходящие моменты времени в состав триггеров (и других синхронных узлов) вводят специальный вход разрешения записи CE (от ClockEnable – «разрешение тактового сигнала»). Перезапись состояния триггера происходит только в том случае, если в момент прихода фронта тактового сигнала на входе CE присутствовал высокий логический уровень.

Необходимо иметь в виду, что действительный уровень сигнала, разрешающего работу синхронных устройств, может быть как логическим нулем, так и логической единицей. В схемотехнике ТТЛ существует целый ряд соображений, по которым некоторые сигналы считаются активными, если их уровень соответствует логическому нулю. Такие сигналы обозначают символом инверсии (небольшой кружок на входе, аналогично выходу инвертора), чертой над именем сигнала на его графическом изображении, а в текстовых описаниях – символами ~ # n перед именем сигнала (например, ~CE, #CE, nCE). Уровень сигнала, при котором соответствующий вход считается влияющим на работу устройства, называют активным уровнем сигнала. Пример изображения D-триггера с входом разрешения тактового сигнала, имеющим активный низкий уровень, приведен на рис. 1.10.

На практике в современных цифровых микросхемах управляющие сигналы чаще имеют высокий активный уровень.

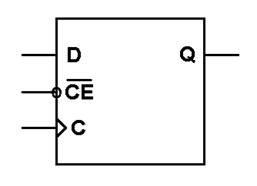
Рис. 1.10 Графическое изображение D-триггера с входом разрешения тактового сигнала, имеющим активный низкий уровень.

Аналогично, активный низкий уровень можно назначить и другим входам и выходам цифровых устройств. Например, если инвертировать тактовый вход D-триггера, то перезапись выхода Q будет происходить при переходе тактового сигнала от уровня единицы к уровню нуля («по спаду тактового сигнала»).

С помощью триггеров можно создавать ряд широко используемых цифровых узлов, например, регистры и счетчики. Под регистром в процессорной технике понимают узел для хранения значения переменной состояния. Это может быть как регистр в понимании программиста, так и внутренние сигналы, кодирующие состояние процессора, недоступные программисту. Все эти устройства в своей основе имеют триггер. Если объединить тактовые входы у нескольких триггеров, то запись в них будет происходить одновременно.

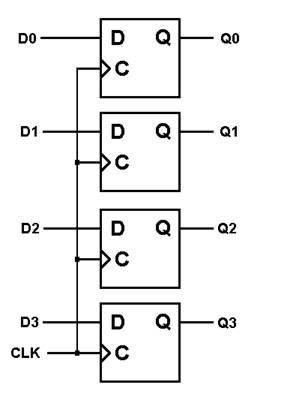
Рис. 1.11. Соединение D-триггеров для получения 4-разрядного регистра.

В схеме, показанной на рис.1.11, четыре триггера формируют устройство для хранения 4-разрядного двоичного числа. Новое значение в регистр записывается по фронту тактового сигнала. Каждый триггер может иметь также вход разрешения записи, и при объединении этих входов образуется вход разрешения записи в регистр, что позволяет перезаписывать значение регистра только в моменты, предусмотренные разработчиком схемы.

 = Перейти к содержанию =