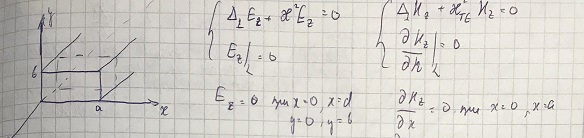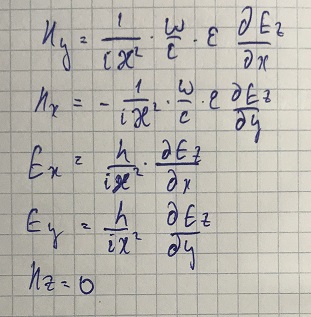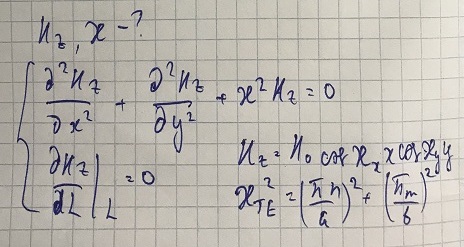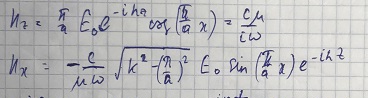Поперечное волновое число.

     Рассмотрим прямоугольный волновод размерами сечения а и b. Запишем для полей в этом волноводе уравнения Гельмгольца и укажем граничные условия:

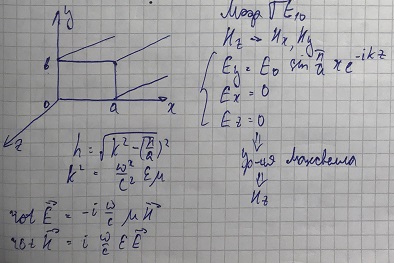
 Для волны типа ТМ имеем следующие компоненты полей:

Найдём для этой моды поперечное волновое число .

   Распишем первую систему по поперечным координатам и представим продольную компоненту в виде:

   Ez = X(x)*Y(y). Используя граничные условия для Ez, найдём компоненты поперечного волнового числа:

 где мы определили две константы. Они отвечают за амплитуду волны и могут быть любыми, так как источники не заданы.

Для ТЕ волн поперечное волновое число находится аналогичным образом:

                                          Бегущие волны.

   Главный интерес представляют бегущие волны в волноводе.

   Какая из мод имеет в прямоугольном волноводе с идеально проводящими стенками наименьшую критическую частоту? ( не равна нулю).

   Условие критической частоты: h = 0. Следовательно:

 

 Минимальной критической частоте соответствует минимальное волновое число.

   - Для случая ТМ волн, если либо x, либо y равна нулю, то Еz = 0 (в силу свойств синуса).
   - Для случая ТЕ волн, если x или у обращаются в ноль, то Нz в ноль не обращается.
   Поэтому волна с минимальной критической частотой - это волна типа ТЕ с индексами (0,1) или (1,0). Также такая волна называется низшей модой. Высшие моды в волноводах используются редко.  

   

                             Нахождение поля волны типа ТЕ10. 

   Рассмотрим волновод, в котором бежит волна моды ТЕ10.

Используя уравнения Максвелла, найдём поперечные компоненты магнитного поля:

 Получаем:

   С помощью приборов измеряют мгновенные значения полей.
   Мгновенные значения - это значения, которые получают путём домножения комплексных амплитуд на exp(iwt) и выделения действительной части полученных выражений.

 

Задания для самостоятельной работы по схеме таксономии Блума.

Знание и понимание
  • Вспомните, что из себя представляет волновое число.
  •  Опишите алгоритм нахождения поперечного волнового числа.
Интеллектуальные навыки
  • Продемонстрируйте на практической задаче выполнение этого алгоритма (для типа волны TE10)
  •  Решите эту же задачу для моды ТЕ01. Что изменилось?
  •  Систематизируйте материал изученной лекции, представив ее в виде развернутой (подробной) интеллект-карты.
  • Сравните свою карту с работами одногруппников. При необходимости дополните ее недостающими пунктами или поделитесь оригринальными пунктами своей краты с другими.

ПРОЙТИ ТЕСТ

Перейти к следующей лекции