
Телеграфные уравнения - пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи.
Погонный параметр - это величина, приходящаяся на единицу длины.
Рассмотрим коаксиальную линию:
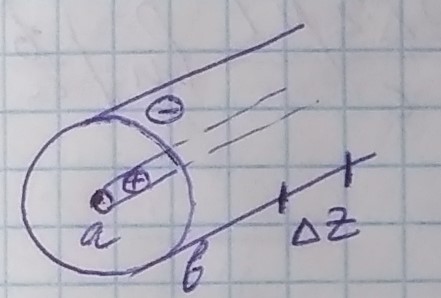
Для нее
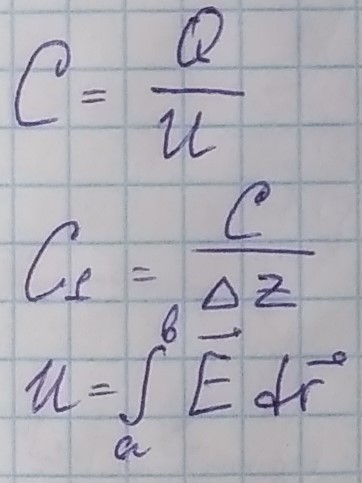 ,
,
где Q - заряд, U - разность потенциалов.
Е ищем с помощью теоремы Гауса :

Тогда
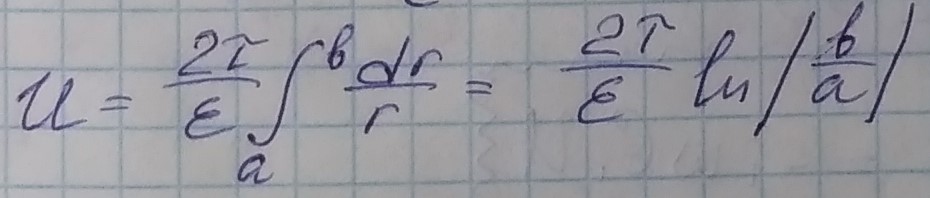
Погонная емкость коаксиальной линии :
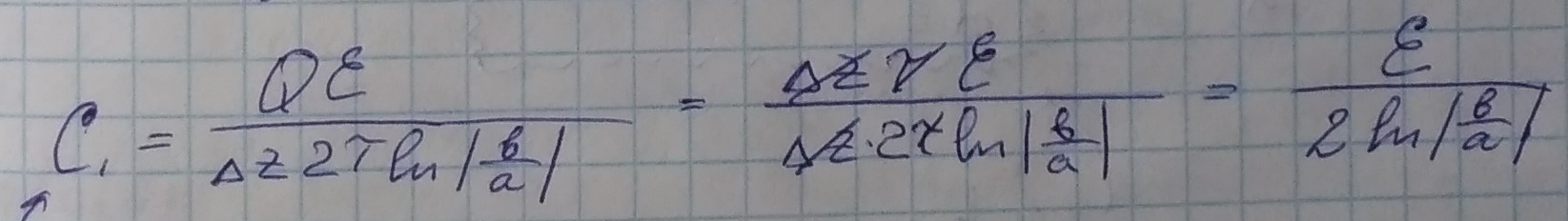
Теперь определеим погонную индуктивность :
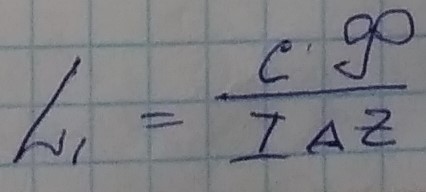 ,
,
где I - ток, протекающий по 1 из проводников, с - скорость света, Ф - поток.
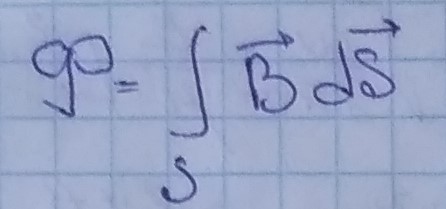
Поток считается через заштрихованную поверхность
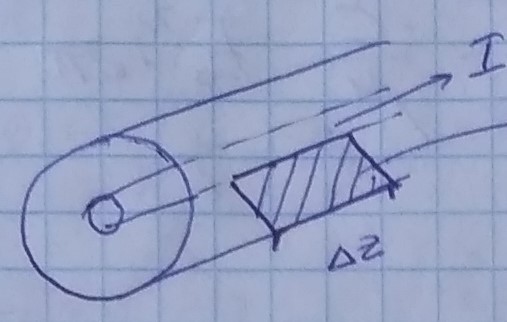

Замкнутый контур выбирают так , чтобы легче было считать, т.е. совпадающим с любой из силовых линий.
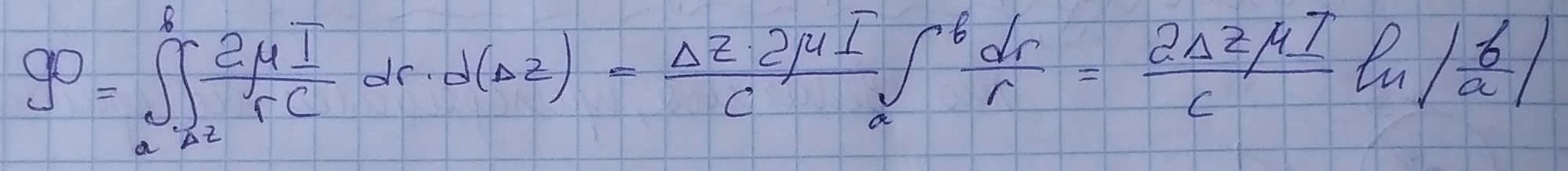
В итоге получаем формулу погонной индуктивности:
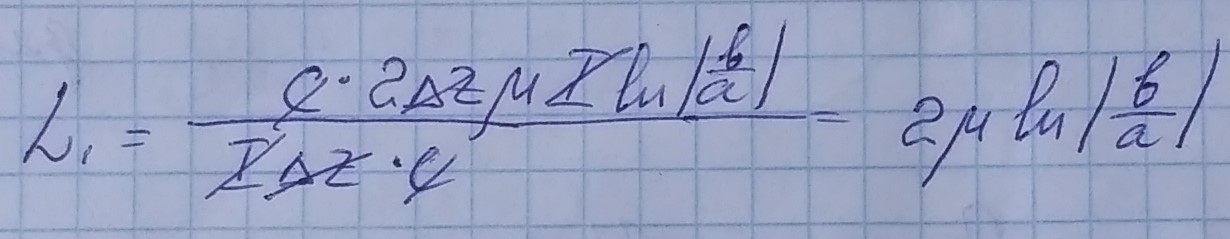

уравнение непрерывности
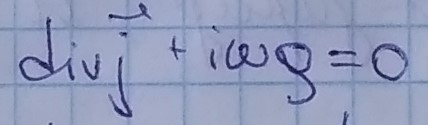
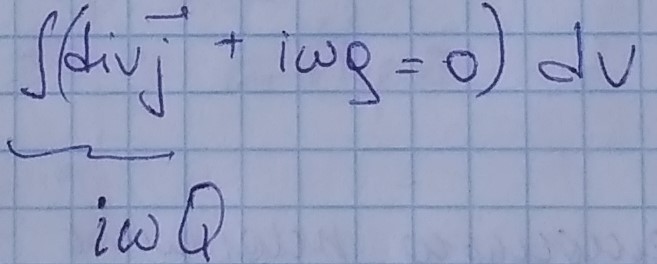
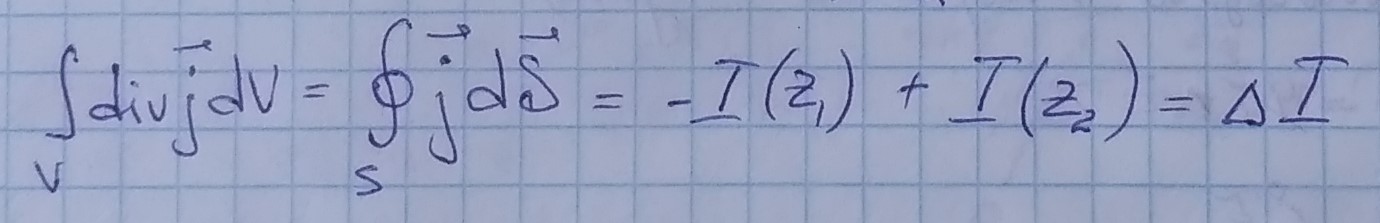
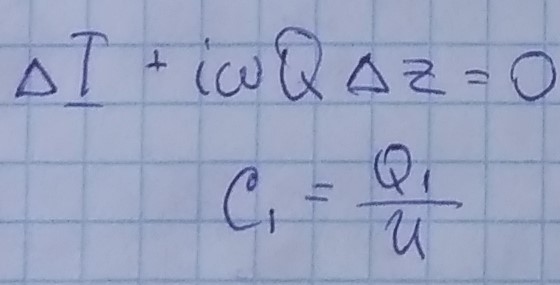
ΔZ → 0
Первое телеграфное уравнение:
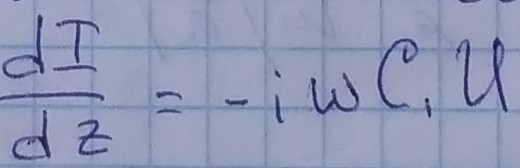
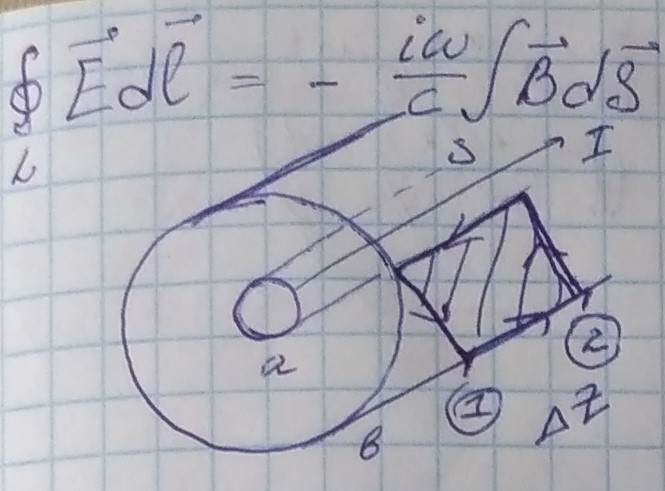
т.к. Еτ = 0 , то все поверхностные компоненты вектором, содержащих тангенциальную компоненту =0
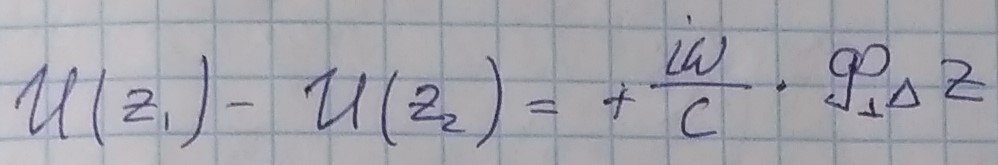
ΔZ → 0
Второе телеграфное уравнение:
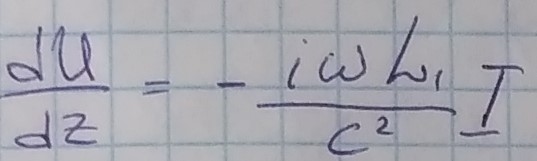
Рассмотрим волну, бегущую по оси OZ.
Для бегущей волны вводят понятие волновое сопротивление линии.
Волновое сопротивление линии - величина, определяемая отношением напряжения падающей волны к току этой волны в линии передачи .
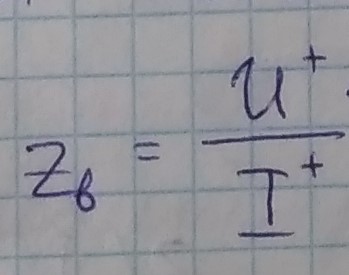
U+ - напряжение в бегущей волне , I+ - ток в бегущей волне
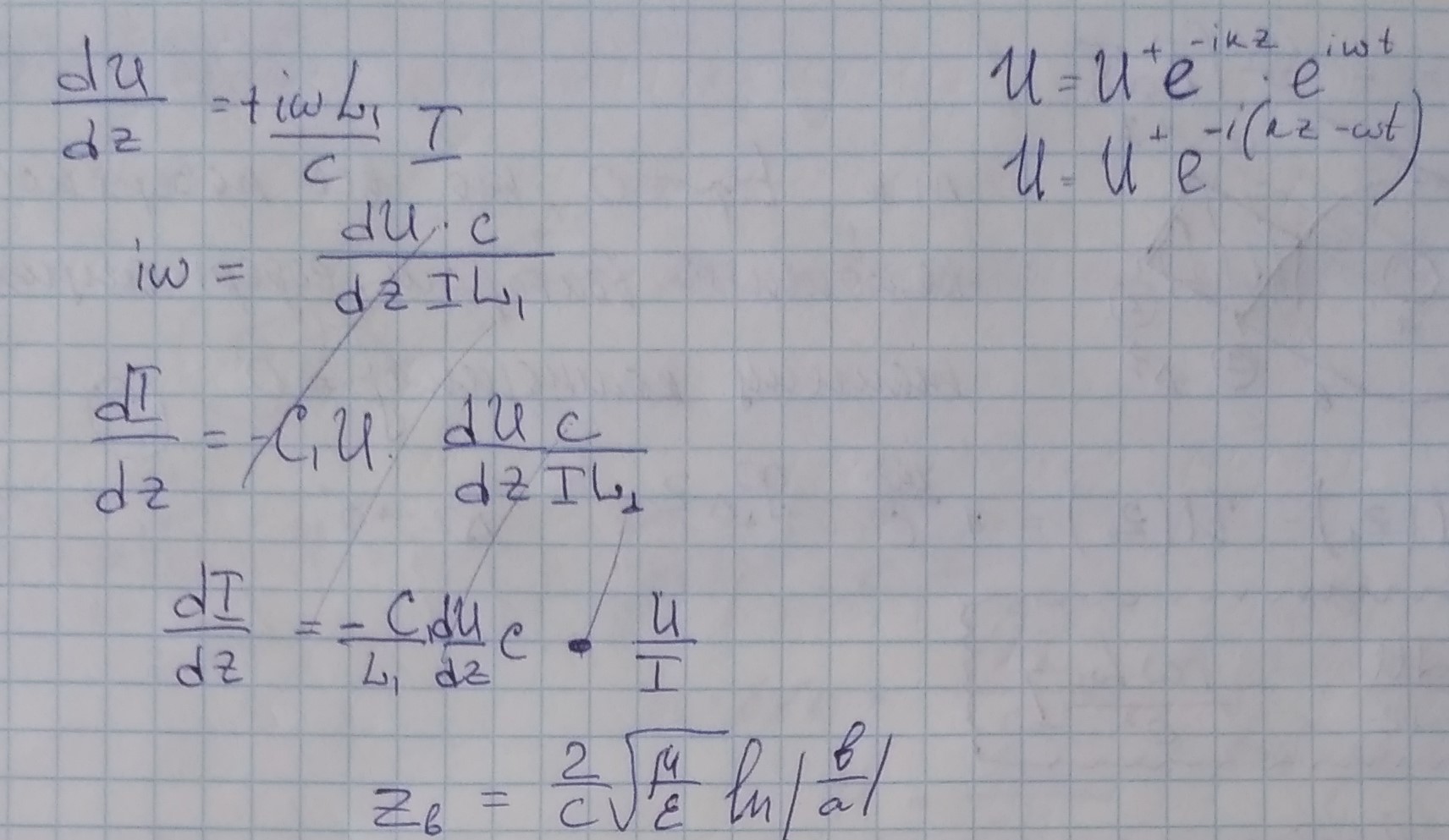
Zв определяется конфигурацией проводников.