Выражения, представляющие поперечные компоненты полей TM волны через произодные от продольных компонент в векторном виде:

• С помощью ТЕМ волн можно передавать любые низкочастотные сигналы.
•  и  ТЕМ волн не зависят от частоты (что обеспечивает нескажение импульса). 

   Сделаем замену переменных:

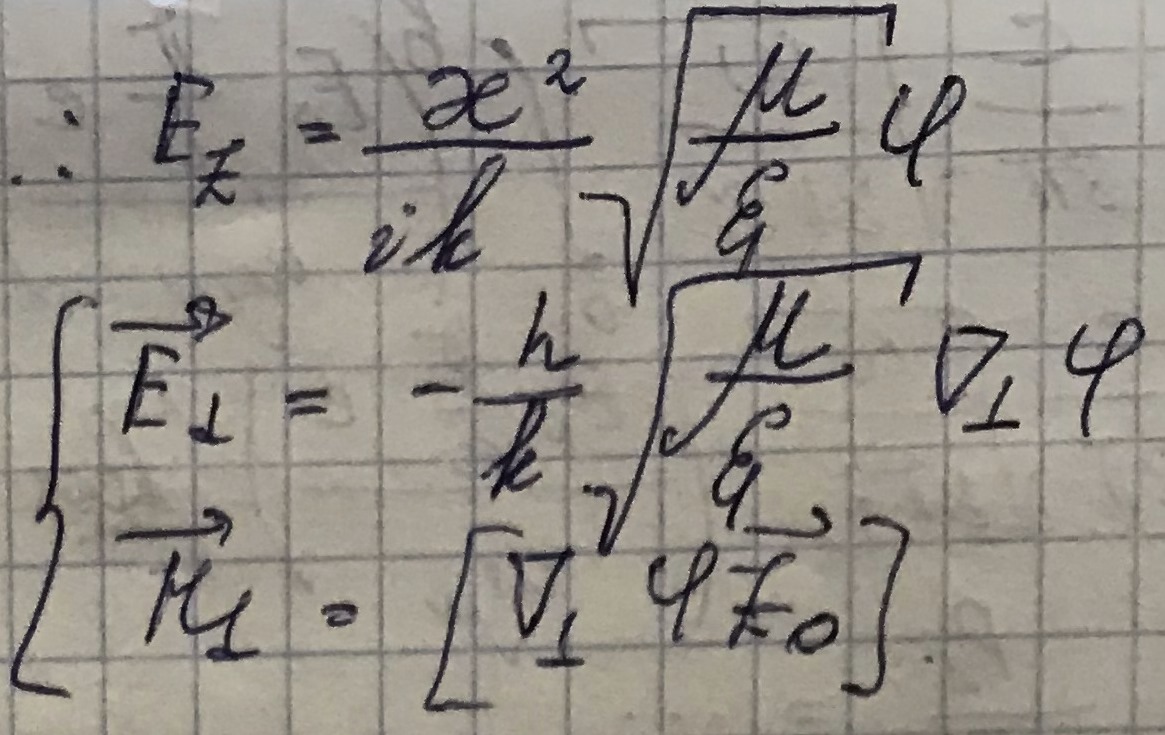
Е_z = 0, так как  = 0.

   Формулы одинаковые, но поля - разные. В одном случае поля - статические(не зависят от времени), в другом - выражаются через комплексные амплитуды.

Из уравнений Максвелла:

   Чтобы найти моды ТЕМ волны, нужно проверить, существуют ли внутри волновода статические поля. Внутри прямоугольного волновода их нет(так как он замкнут), следовательно ТЕМ волн в нём нет.

                      Нахождение полей в ТЕМ волнах.

   Алгоритм:

1) Рассматриваем статическое поле (используем теорему Гаусса или теорему о циркуляции).

2) Записываем ТЕМ поле с аналогичной зависимостью от поперечных координат.

3) Находим остальные компоненты поля ТЕМ.

Нужно "посадить" положительный заряд с линейной плотностью на внутренний проводник, с отрицательносй - на внешний.

        Сделаем предположение, что поле в волноводе - радиально.

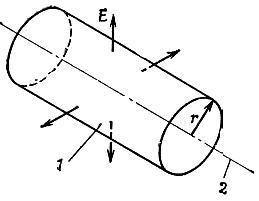
Способ 1: по теореме Гаусса.

Способ 2: используем теорему о циркуляции магнитного поля

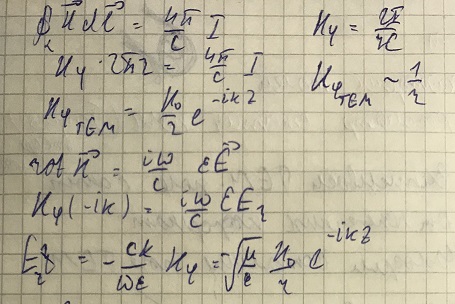
        Таким образом, мы нашли поля ТЕМ волны двумя равноправными способами. 

   Используем найденные поля для решения следующей задачи.

   Задача.

   Дан коаксиальный волновод, у которого стенки, и внутренние, и внешние, - не идеально проводящие. Найдём коэффициент затухания h''.

               Уравнения длинных линий (телеграфные уравнения).

   Телеграфные уравнения — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока по времени и расстоянию в линиях электрической связи.

   По теореме Гаусса имеем:

   L₁, С₁ - погонные индуктивность и ёмкость соответственно. 

Таким образом, .

   Рассмотрим уравнение непрерывности:

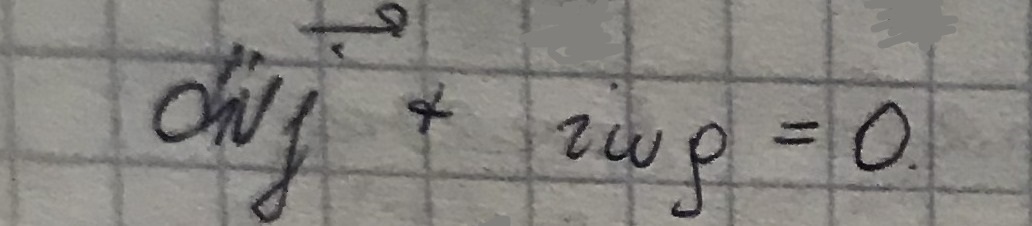
   Интегрируя выражения по объему куска волновода, получим:

                            Волновое сопротивление линии.

   Запишем уравнения Гельмгольца:

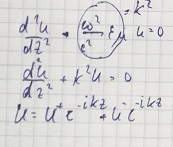
   Рассмотрим одну из волн. Пусть она бежит по оси Z. Для бегущей волны вводят понятие волнового сопротивления линии, которое равно соотношению:

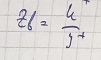
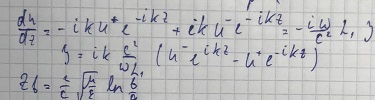
 Характеристический импеданс в длинных линиях от конфигурации не зависит, а зависит от волнового импеданса Z_в.

                       Формула пересчёта импедансов.

Задания для самостоятельной работы по схеме таксономии Блума.

ПРОЙТИ ТЕСТ

Перейти к следующей лекции